Точки Аполлония: различия между версиями
Перейти к навигации
Перейти к поиску
| [отпатрулированная версия] | [непроверенная версия] |
Содержимое удалено Содержимое добавлено
| Строка 14: | Строка 14: | ||
* Пусть ''ABC'' — треугольник на плоскости. Окружность, проходящая через [[центроид]] и две точки Аполлония треугольника ''ABC'', называется '''[[Точка Парри|окружностью Парри]]''' треугольника ''ABC'' (на рисунке справа она красная). Она также проходит через ''точку Парри'' (красная точка в черном кольце). |
* Пусть ''ABC'' — треугольник на плоскости. Окружность, проходящая через [[центроид]] и две точки Аполлония треугольника ''ABC'', называется '''[[Точка Парри|окружностью Парри]]''' треугольника ''ABC'' (на рисунке справа она красная). Она также проходит через ''точку Парри'' (красная точка в черном кольце). |
||
* Рассмотрим три сферы, касающиеся плоскости в точках <math>A, B, C </math> и друг друга внешним образом. Если радиусы этих сфер равны <math> x, y, z</math>, то <math>AB = \sqrt{xy}</math> и т. д. Поэтому две сферы касающиеся трёх данных и плоскости, будут касаться плоскости в ''точках Аполлония''. |
* Рассмотрим три сферы, касающиеся плоскости в точках <math>A, B, C </math> и друг друга внешним образом. Если радиусы этих сфер равны <math> x, y, z</math>, то <math>AB = \sqrt{xy}</math> и т. д. Поэтому две сферы касающиеся трёх данных и плоскости, будут касаться плоскости в ''точках Аполлония''. |
||
* '''Кубика |
* '''Кубика [[Нойберг, Жозеф|Нойберга]]''' — множество таких точек <math>X</math>, что <math>XX' \parallel OH</math> — прямой Эйлера (зафиксирована её бесконечно удалённая точка). На этой кубике лежит более 15 замечательных точек, в частности, '''точки''' Торричелли, '''Аполлония''', ортоцентр, центр описанной окружности, вершины правильных треугольников, построенных на сторонах (внешним или внутренним образом), точки, симметричные вершинам относительно сторон, две [[точки Ферма]], две [[изодинамические точки]], бесконечную точку Эйлера, а также лежащие на всех кубиках центры вписанной и вневписанных окружностей. В списке '''кубик плоского треугольника''' Берхарта Гиберта<!--(Berhard Gibert)-->'' кубика Нейберга'' значится как '''K001'''<ref>'''K001''' at Berhard Gibert’s '''Cubics in the Triangle Plane'''// [http://pagesperso-orange.fr/bernard.gibert/Exemples/k001.html] {{Wayback|url=http://pagesperso-orange.fr/bernard.gibert/Exemples/k001.html |date=20090820221517 }}</ref>. |
||
== См. также == |
== См. также == |
||
Версия от 02:18, 22 сентября 2022

Точки Аполлония (иногда изодинамические центры[1]) — две такие точки, расстояние от которых до вершин треугольника обратно пропорциональны сторонам, которые противолежат этим вершинам.
Свойства
- Точки Аполлония это центры инверсии, которые преобразуют данный треугольник в равносторонний треугольник.
- Окружности, построенные как на диаметре на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
- Точки Аполлония лежат на прямой, соединяющей центр описанной окружности с точкой Лемуана. Эта прямая называется осью Брокара.
- Подерные треугольники точек Аполлония правильные (иногда это свойство принимается за определение).
- Последнее свойство можно сформулировать иначе: три ортогональные проекции точек Аполлония на стороны данного треугольника являются вершинами правильного треугольника.
- Точки Аполлония изогонально сопряжены точкам Торричелли.
- Построим две прямые, каждая из которых проходит через точку Аполлония и точку Торричелли, отличную от изогонально сопряжённой ей. Такие прямые пересекутся в точке пересечения медиан (в центроиде треугольника).
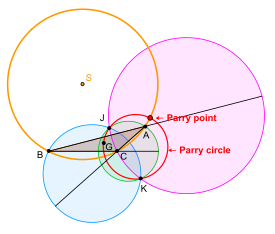
- Пусть ABC — треугольник на плоскости. Окружность, проходящая через центроид и две точки Аполлония треугольника ABC, называется окружностью Парри треугольника ABC (на рисунке справа она красная). Она также проходит через точку Парри (красная точка в черном кольце).
- Рассмотрим три сферы, касающиеся плоскости в точках и друг друга внешним образом. Если радиусы этих сфер равны , то и т. д. Поэтому две сферы касающиеся трёх данных и плоскости, будут касаться плоскости в точках Аполлония.
- Кубика Нойберга — множество таких точек , что — прямой Эйлера (зафиксирована её бесконечно удалённая точка). На этой кубике лежит более 15 замечательных точек, в частности, точки Торричелли, Аполлония, ортоцентр, центр описанной окружности, вершины правильных треугольников, построенных на сторонах (внешним или внутренним образом), точки, симметричные вершинам относительно сторон, две точки Ферма, две изодинамические точки, бесконечную точку Эйлера, а также лежащие на всех кубиках центры вписанной и вневписанных окружностей. В списке кубик плоского треугольника Берхарта Гиберта кубика Нейберга значится как K001[2].
См. также
- Аполлоний Пергский
- Геометрия треугольника
- Замечательные точки треугольника
- Задача Аполлония
- Изодинамические центры = Isodynamic point (англ.)
- Окружность Аполлония
- Окружность Парри
- Теорема Аполлония
- Точки Торричелли
- Точка Ферма
- Треугольник
- Отрезки и окружности, связанные с треугольником
- Точка Аполлония
Примечания
- ↑ Katarzyna Wilczek. The harmonic center of a trilateral and the Apollonius point of a triangle (англ.) // Journal of Mathematics and Applications : journal. — 2010. — Vol. 32. — P. 95—101.
- ↑ K001 at Berhard Gibert’s Cubics in the Triangle Plane// [1] Архивная копия от 20 августа 2009 на Wayback Machine
Ссылки
- Moon, Tarik Adnan (2010), "The Apollonian circles and isodynamic points" (PDF), Mathematical Reflections (6), Архивировано (PDF) 20 апреля 2013 Архивная копия от 20 апреля 2013 на Wayback Machine.




