Потенциал Сазерленда: различия между версиями

Интерактивная навигация по истории

(Показать все непатрулированные изменения)

[отпатрулированная версия]

← Предыдущая правка Следующая правка →

Содержимое удалено Содержимое добавлено

ВизуальныйВики-текст

Линейный

Версия от 10:34, 27 февраля 2024

Потенциал Сазерленда^{[ссылка 1]}^{[ссылка 2]} (Sutherland potential) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния $r$ между ними. Эта модель относительно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании. Впервые этот вид потенциала был предложен Уильямом Сазерлендом^[англ.] в 1893 году.

Вид потенциала взаимодействия

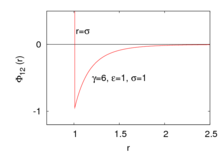
Уильям Сазерленд получил более реалистичное выражение для потенциала взаимодействия, чем полученное из потенциала бесконечно жестких упругих сфер. Данный потенциал описывается следующим выражением:

\Phi _{2}(r)={\begin{cases}\infty ,{\phantom {mmm,}}r\leq \sigma \\-\varepsilon \left({\dfrac {\sigma }{r}}\right)^{\gamma },r>\sigma \end{cases}},

где $\Phi _{2}(r)$ — потенциал парного взаимодействия^{[комментарий 1]}, $r=|{\boldsymbol {r_{1}}}-{\boldsymbol {r_{2}}}|$ — расстояние между частицами 1 и 2, положение которых описывается радиусом-вектором ${\boldsymbol {r}}$ . $\varepsilon$ — глубина потенциальной ямы, $\sigma$ — радиус соответствующей твёрдой сферы, $\gamma$ — параметр, контроллирующий скорость убывания потенциала до нуля.

Данный потенциал, в отличие от потенциала Леннарда-Джонса, является «притягивательным», то есть описывающим лишь притяжение частиц в силу того, что на больших расстояниях $F_{2}=-{\frac {{\text{d}}\Phi _{2}(r)}{{\text{d}}r}}\leq 0$ . Отталкивание частиц происходит лишь на расстояниях, $r\leq \sigma$ с бесконечной силой.

Примечания

Комментарии

↑ Intermolecular pair potential on SklogWiki.

Источники

↑ William Sutherland. The viscosity of gases and molecular force // Philosophical Magazine. — 1893. — Т. 36. — С. 507—531.
↑ H. W. Graben and R. D. Present. Third Virial Coefficient for the Sutherland (∞, ν) Potential // Reviews of Modern Physics. — 1964. — Т. 36. — С. 1025—1033.

Литература

Каплан И. Г. Введение в теорию межмолекулярных взаимодействий.. — М.: Наука. Главная редакция физико-математической литературы, 1982. — С. 312.
M. P. Allen, D. J. Tildesley. Computer Simulation of Liquids. — Oxford University Press, 1990. — ISBN 0198556454. — ISBN 9780198556459.
Цянь Сюэ-Сень. Физическая механика. — М.: Мир, 1965. — 544 с.
D. Levi and M. de Llano. Closed form of second virial coefficient for Sutherland potential // Journal of Chemical Physics. — 1975. — Т. 63. — С. 4561—4562.
Jianxiang Tian and Yuanxing Gui. Liquid-gas phase transition to first order of an argon-like fluid modeled by the hard-core similar Sutherland potential // International Journal of Modern Physics B. — 2004. — Т. 18. — С. 2057—2069.
A. Díez, J. Largo and J. R. Solana. Structure and thermodynamic properties of Sutherland fluids from computer simulation and the Tang–Lu integral equation theory // Fluid Phase Equilibria. — 2007. — № 253. — С. 67—73.
Jianguo Mi, Yiping Tang, and Chongli Zhong. Theoretical study of Sutherland fluids with long-range, short-range, and highly short-range potential parameters // Journal of Chemical Physics. — 2008. — Т. 128. — С. 054503.
Roman Melnyk, Pedro Orea, Ivo Nezbeda, and Andrij Trokhymchuk. Liquid/vapor coexistence and surface tension of the Sutherland fluid with a variable range of interaction: Computer simulation and perturbation theory studies // Journal of Chemical Physics. — 2010. — № 132. — С. 134504.
F. Paragand, F. Feyzi and B. Behzadi. Application of the SAFT-VR equation of state to vapor–liquid equilibrium calculations for pure components and binary mixtures using the Sutherland potential // Fluid Phase Equilibria. — 2010. — Т. 290. — С. 181—194.

См. также

Ссылки

Sutherland potential on SklogWiki.

[3] Intermolecular pair potential on SklogWiki.

[1] William Sutherland. The viscosity of gases and molecular force // Philosophical Magazine. — 1893. — Т. 36. — С. 507—531.

[2] H. W. Graben and R. D. Present. Third Virial Coefficient for the Sutherland (∞, ν) Potential // Reviews of Modern Physics. — 1964. — Т. 36. — С. 1025—1033.

[ссылка 1]

[ссылка 2]

[комментарий 1]

@@ Строка 1: / Строка 1: @@
+'''Потенциал Сазерленда'''<ref group="ссылка">{{Статья|заглавие=The viscosity of gases and molecular force|издание=Philosophical Magazine|автор=William Sutherland|ссылка=https://www.tandfonline.com/doi/abs/10.1080/14786449308620508|год=1893|том=36|страницы=507—531}}</ref><ref group="ссылка">{{Статья|заглавие=Third Virial Coefficient for the Sutherland (∞, ν) Potential|издание=Reviews of Modern Physics|автор=H. W. Graben and R. D. Present|ссылка=https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.36.1025|год=1964|том=36|страницы=1025—1033}}</ref> (Sutherland potential) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния <math>r</math> между ними. Эта модель относительно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании. Впервые этот вид потенциала был предложен {{Iw|Сазерленд, Уильям (физик)|Уильямом Сазерлендом|4=William Sutherland (physicist)}} в 1893 году.
-'''Потенциал Сазерленда'''<ref group="ссылка">{{Статья|заглавие=The viscosity of gases and molecular force|издание=Philosophical Magazine|автор=William Sutherland|ссылка=https://www.tandfonline.com/doi/abs/10.1080/14786449308620508|год=1893|том=36|страницы=507-531}}</ref><ref group="ссылка">{{Статья|заглавие=Third Virial Coefficient for the Sutherland (∞, ν) Potential|издание=Reviews of Modern Physics|автор=H. W. Graben and R. D. Present|ссылка=https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.36.1025|год=1964|том=36|страницы=1025-1033}}</ref> (Sutherland potential) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния <math>r</math> между ними. Эта модель относительно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании. Впервые этот вид потенциала был предложен [[Уильям Сазерленд|Уильямом Сазерлендом]] в 1893 г.
 == Вид потенциала взаимодействия ==
@@ Строка 11: / Строка 10: @@
 \end{cases},
 </math>
-где <math>\Phi_2(r)</math> — [[Потенциал парного взаимодействия|потенциал парного взаимодействия]]<ref group="комментарий">[http://www.sklogwiki.org/SklogWiki/index.php/Intermolecular_pair_potential Intermolecular pair potential] on [http://www.sklogwiki.org SklogWiki].</ref>, <math>r=|\boldsymbol{r_1}-\boldsymbol{r_2}|</math> — расстояние между частицами 1 и 2, положение которых описывается радиусом-вектором <math>\boldsymbol{r}</math>. <math>\varepsilon</math> — глубина [[Потенциальная яма|потенциальной ямы]], <math>\sigma</math> — радиус соответствующей твёрдой сферы, <math>\gamma</math> — параметр, контроллирующий скорость убывания потенциала до нуля.
+где <math>\Phi_2(r)</math> — [[потенциал парного взаимодействия]]<ref group="комментарий">[http://www.sklogwiki.org/SklogWiki/index.php/Intermolecular_pair_potential Intermolecular pair potential] on [http://www.sklogwiki.org SklogWiki].</ref>, <math>r=|\boldsymbol{r_1}-\boldsymbol{r_2}|</math> — расстояние между частицами 1 и 2, положение которых описывается радиусом-вектором <math>\boldsymbol{r}</math>. <math>\varepsilon</math> — глубина [[Потенциальная яма|потенциальной ямы]], <math>\sigma</math> — радиус соответствующей твёрдой сферы, <math>\gamma</math> — параметр, контроллирующий скорость убывания потенциала до нуля.
-Данный потенциал, в отличие от [[Потенциал Леннарда-Джонса|потенциала Леннарда-Джонса]], является "притягивательным", т.е. описывающим лишь притяжение частиц в силу того, что на больших расстояниях <math>F_2=-\frac{\text{d}\Phi_2(r)}{\text{d}r}\le0</math>. Отталкивание частиц происходит лишь на расстояниях, <math>r\le\sigma</math> с бесконечной силой.
+Данный потенциал, в отличие от [[Потенциал Леннарда-Джонса|потенциала Леннарда-Джонса]], является «притягивательным», то есть описывающим лишь притяжение частиц в силу того, что на больших расстояниях <math>F_2=-\frac{\text{d}\Phi_2(r)}{\text{d}r}\le0</math>. Отталкивание частиц происходит лишь на расстояниях, <math>r\le\sigma</math> с бесконечной силой.
 == Примечания ==
@@ Строка 28: / Строка 27: @@
 * {{Книга|заглавие=Computer Simulation of Liquids|автор=M. P. Allen, D. J. Tildesley|издательство=Oxford University Press|год=1990|isbn=0198556454|isbn2=9780198556459}}
 * {{книга | автор  = Цянь Сюэ-Сень | заглавие = Физическая механика | место = М. | издательство = Мир | год = 1965 | страниц = 544 | isbn =  | ref = Цянь}}
-* {{Статья|заглавие=Closed form of second virial coefficient for Sutherland potential|издание=Journal of Chemical Physics|автор=D. Levi and M. de Llano|ссылка=http://dx.doi.org/10.1063/1.431141|год=1975|том=63|страницы=4561-4562}}
+* {{Статья|заглавие=Closed form of second virial coefficient for Sutherland potential|издание=Journal of Chemical Physics|автор=D. Levi and M. de Llano|ссылка=http://dx.doi.org/10.1063/1.431141|год=1975|том=63|страницы=4561—4562}}
-* {{Статья|заглавие=Liquid-gas phase transition to first order of an argon-like fluid modeled by the hard-core similar Sutherland potential|издание=International Journal of Modern Physics B|автор=Jianxiang Tian and Yuanxing Gui|ссылка=http://dx.doi.org/10.1142/S0217979204025142|год=2004|том=18|страницы=2057-2069}}
+* {{Статья|заглавие=Liquid-gas phase transition to first order of an argon-like fluid modeled by the hard-core similar Sutherland potential|издание=International Journal of Modern Physics B|автор=Jianxiang Tian and Yuanxing Gui|ссылка=http://dx.doi.org/10.1142/S0217979204025142|год=2004|том=18|страницы=2057—2069}}
-* {{Статья|заглавие=Structure and thermodynamic properties of Sutherland fluids from computer simulation and the Tang–Lu integral equation theory|издание=Fluid Phase Equilibria|автор=A. Díez, J. Largo and J. R. Solana|ссылка=http://dx.doi.org/10.1016/j.fluid.2007.01.011|год=2007|номер=253|страницы=67-73}}
+* {{Статья|заглавие=Structure and thermodynamic properties of Sutherland fluids from computer simulation and the Tang–Lu integral equation theory|издание=Fluid Phase Equilibria|автор=A. Díez, J. Largo and J. R. Solana|ссылка=http://dx.doi.org/10.1016/j.fluid.2007.01.011|год=2007|номер=253|страницы=67—73}}
 * {{Статья|заглавие=Theoretical study of Sutherland fluids with long-range, short-range, and highly short-range potential parameters|издание=Journal of Chemical Physics|автор=Jianguo Mi, Yiping Tang, and Chongli Zhong|ссылка=http://dx.doi.org/10.1063/1.2828720|год=2008|том=128|страницы=054503}}
 * {{Статья|заглавие=Liquid/vapor coexistence and surface tension of the Sutherland fluid with a variable range of interaction: Computer simulation and perturbation theory studies|издание=Journal of Chemical Physics|автор=Roman Melnyk, Pedro Orea, Ivo Nezbeda, and Andrij Trokhymchuk|ссылка=http://dx.doi.org/10.1063/1.3371710|год=2010|номер=132|страницы=134504}}
-* {{Статья|заглавие=Application of the SAFT-VR equation of state to vapor–liquid equilibrium calculations for pure components and binary mixtures using the Sutherland potential|издание=Fluid Phase Equilibria|автор=F. Paragand, F. Feyzi and B. Behzadi|ссылка=http://dx.doi.org/10.1016/j.fluid.2009.10.027|год=2010|том=290|страницы=181-194}}
+* {{Статья|заглавие=Application of the SAFT-VR equation of state to vapor–liquid equilibrium calculations for pure components and binary mixtures using the Sutherland potential|издание=Fluid Phase Equilibria|автор=F. Paragand, F. Feyzi and B. Behzadi|ссылка=http://dx.doi.org/10.1016/j.fluid.2009.10.027|год=2010|том=290|страницы=181—194}}
 == См. также ==

Потенциал Сазерленда: различия между версиями

Версия от 10:34, 27 февраля 2024

Содержание

Вид потенциала взаимодействия

Примечания

Литература

См. также

Ссылки

Навигация

Потенциал Сазерленда: различия между версиями

Версия от 10:34, 27 февраля 2024

Вид потенциала взаимодействия

Примечания

Литература

См. также

Ссылки

Навигация

Поиск