Струнный граф: различия между версиями
| [отпатрулированная версия] | [непроверенная версия] |
Fuxx (обсуждение | вклад) м образоать=>образовать |
|||
| Строка 171: | Строка 171: | ||
[[Категория:Топологическая теория графов]] |
[[Категория:Топологическая теория графов]] |
||
[[Категория:Графы пересечений]] |
[[Категория:Графы пересечений]] |
||
[[Категория:NP-полные задачи]] |
|||
Версия от 11:10, 30 мая 2024
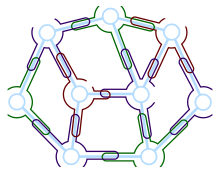
Струнный граф — это граф пересечений кривых на плоскости, каждая кривая при этом называется «струной». Если дан граф G, он является струнным тогда и только тогда, когда существует набор кривых (струн), нарисованных на плоскости, таких, что никакие три струны не пересекаются в одной точке и граф G изоморфен графу, вершины которого соответствуют кривым, а дуга в этом графе соответствует пересечению двух кривых.
Предпосылки
Бензер (Benzer 1959) описывал концепцию, близкую струнным графам, но для более общих структур. В этом контексте он также сформулировал специальный случай пересечения интервалов на прямой, ставший классическим классом интервальных графов. Позднее Синден (Sinden 1966) выразил ту же идеею для электрических сетей и печатных схем. Математическое изучение струнных графов началось со статьи Эрлиха, Ивена и Тарьяна (Ehrlich, Even, Tarjan 1976) и при содействии Синдена и Рональда Грэма описание струнных графов, в конечном счёте, было поставлено как открытая проблема на 5-м Венгерском коллоквиуме по комбинаторике в 1976[1]. В конце концов, было доказано, что распознавание струнных графов является NP-полной задачей, откуда следует, что вряд ли существует простое описание этого класса[2]

Связанные классы графов
Любой планарный граф является струнным[3] — можно образовать представление в виде струнного графа для любого вложенного в плоскость графа путём рисования для каждой вершины кривой, которая обходит по кругу вершину и середину каждого смежного ребра, как показано на рисунке. Для любого ребра uv графа, струны для u и v пересекаются дважды близ середины ребра uv, и не существует других пересечений, так что пересечение пары струн представляют смежные пары вершин исходного планарного графа. Альтернативно, по теореме об упаковке кругов, любой планарный граф может быть представлен в виде коллекции окружностей, любые две из которых пересекаются тогда и только тогда, когда соответствующие вершины смежны. Эти окружности (с начальной и конечной точкой, выбранными для превращения окружности в открытую кривую) дают представление заданного планарного графа в виде струнного графа. Чалопин, Гонсалвис и Ошан (Chalopin, Gonçalves, Ochem 2007) доказали, что любой планарный граф имеет представление в виде струнного графа, в котором каждая пара струн имеет максимум одно пересечение, а не так, как описано выше. Гипотеза Шейнермана, ныне доказанная, является даже более строгим утверждением, что любой планарный граф может быть представлен как граф пересечений отрезков. x Если все рёбра заданного графа G подразделяются, полученный граф является струнным графом тогда и только тогда, когда граф G планарен. В частности, подразделение полного графа K5, показанное на рисунке, струнным графом не является, поскольку K5 не планарен[3].
Любой круговой граф, как граф пересечений отрезков (хорд окружности) является также струнным графом. Любой хордальный граф может быть представлен как струнный граф — хордальные графы являются графами пересечений поддеревьев деревьев и можно образовать струнное представление хордального графа путём планарного вложения соответствующего дерева и заменой каждого поддерева струной, проходящей вокруг рёбер поддерева.
Дополнение графа любого графа сравнимости является также струнным графом[4].
Другие результаты
Эрлих, Эвен и Тарьян (Ehrlich, Even, Tarjan 1976) показали, что вычисление хроматического числа струнного графа является NP-трудной задачей. Кратохвил (Kratochvil 1991a) обнаружил, что струнные графы образуют замкнутый класс порождённых миноров, но не минорно замкнутый класс графов.
Любой струнный граф с m рёбрами можно разбить на два подмножества, при этом каждое подмножество составляет фиксированную долю полного графа, путём удаления O(m3/4log1/2m) рёбер. Отсюда следует, что струнные графы без клик, струнные графы, не содержащие подграфов Kt,t ни для какой постоянной t, имеют O(n) рёбер и имеют полиномиальное расширение[5][6].
Примечания
- ↑ Graham, 1976.
- ↑ Кратохвил (Kratochvil 1991b) показал, что распознавание струнного графа является NP-трудной задачей, но не смог показать, что она может быть решена в классе NP. После промежуточных результатов Шефера и Стефанковича (Schaefer, Štefankovič 2001), Паха и Тота (Pach, Tóth 2002), Шефера, Седжвика и Стефанковича (Schaefer, Sedgwick, Štefankovič 2003) было завершено доказательство, что задача NP-полна.
- ↑ 1 2 Шефер и Стефанкович (Schaefer, Štefankovič 2001) приписывают это наблюдение Синдену(Sinden 1966).
- ↑ Golumbic, Rotem, Urrutia, 1983; Lovász, 1983. См. также статью Фокса и Паха (Fox, Pach 2009).
- ↑ Fox, Pach, 2009.
- ↑ Dvořák, Norin, 2015.
Литература
- S. Benzer. On the topology of the genetic fine structure // Proceedings of the National Academy of Sciences of the United States of America. — 1959. — Т. 45, вып. 11. — С. 1607–1620. — doi:10.1073/pnas.45.11.1607. — .
- J. Chalopin, D. Gonçalves, P. Ochem. Planar graphs are in 1-STRING // Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. — ACM and SIAM, 2007. — С. 609–617.
- Zdeněk Dvořák, Sergey Norin. Strongly sublinear separators and polynomial expansion. — 2015. — arXiv:1504.04821.
- G. Ehrlich, S. Even, R. E. Tarjan. Intersection graphs of curves in the plane // Journal of Combinatorial Theory. — 1976. — Т. 21, вып. 1. — С. 8–20. — doi:10.1016/0095-8956(76)90022-8.
- Jacob Fox, János Pach. A separator theorem for string graphs and its applications // Combinatorics, Probability and Computing. — 2009. — Т. 19, вып. 3. — С. 371. — doi:10.1017/s0963548309990459.
- M. Golumbic, D. Rotem, J. Urrutia. Comparability graphs and intersection graphs // Discrete Mathematics. — 1983. — Т. 43, вып. 1. — С. 37–46. — doi:10.1016/0012-365X(83)90019-5.
- R. L. Graham. Problem 1 // Open Problems at 5th Hungarian Colloquium on Combinatorics. — 1976.
- Jan Kratochvil. String Graphs. I. The number of critical nonstring graphs is infinite // Journal of Combinatorial Theory, Series B. — 1991a. — Т. 52, вып. 1. — С. 53–66. — doi:10.1016/0095-8956(91)90090-7.
- Jan Kratochvil. String Graphs. II. Recognizing string graphs is NP-Hard // Journal of Combinatorial Theory, Series B. — 1991b. — Т. 52, вып. 1. — С. 67–78. — doi:10.1016/0095-8956(91)90091-W.
- L. Lovász. Perfect graphs // Selected Topics in Graph Theory. — London: Academic Press, 1983. — Т. 2. — С. 55–87.
- János Pach, Geza Tóth. Recognizing string graphs is decidable // Discrete and Computational Geometry. — 2002. — Т. 28, вып. 4. — С. 593–606. — doi:10.1007/s00454-002-2891-4.
- Marcus Schaefer, Daniel Štefankovič. Decidability of string graphs // Proceedings of the 33rd Annual ACM Symposium on the Theory of Computing (STOC 2001). — 2001. — С. 241–246.
- Marcus Schaefer, Eric Sedgwick, Daniel Štefankovič. Recognizing string graphs in NP // Journal of Computer and System Sciences. — 2003. — Т. 67, вып. 2. — С. 365–380. — doi:10.1016/S0022-0000(03)00045-X.
- F. W. Sinden. Topology of thin film RC-circuits // Bell System Technical Journal. — 1966. — Т. 45. — С. 1639–1662. — doi:10.1002/j.1538-7305.1966.tb01713.x.
Для улучшения этой статьи желательно:
|