Сингония: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Ludvig14 (обсуждение | вклад) отмена правки 21267406 участника 89.232.105.24 (обс) та самая путаница сингония-крист.система |
|||
| Строка 3: | Строка 3: | ||
== Категоризация == |
== Категоризация == |
||
Элементарная ячейка кристалла строится на трёх [[компланарные вектора|некомпланарных]] векторах <math>~\mathbf a, \mathbf b, \mathbf c</math>, называемых [[Трансляция (кристаллография)|трансляциями]]. В зависимости от соотношения между длинами этих трансляций и углами между ними <math>~\alpha, \beta, \gamma</math> выделяют '' |
Элементарная ячейка кристалла строится на трёх [[компланарные вектора|некомпланарных]] векторах <math>~\mathbf a, \mathbf b, \mathbf c</math>, называемых [[Трансляция (кристаллография)|трансляциями]]. В зависимости от соотношения между длинами этих трансляций и углами между ними <math>~\alpha, \beta, \gamma</math> выделяют ''шесть'' различных сингоний, которые распадаются на три категории в зависимости от числа равных длин трансляций: |
||
* Низшая категория (все трансляции не равны друг другу) |
* Низшая категория (все трансляции не равны друг другу) |
||
| Строка 20: | Строка 20: | ||
** [[Гексагональная сингония|Гексагональная]]: <math>a=b \ne c</math>, <math>~\alpha = \beta =90^\circ, \gamma = 120^\circ</math> |
** [[Гексагональная сингония|Гексагональная]]: <math>a=b \ne c</math>, <math>~\alpha = \beta =90^\circ, \gamma = 120^\circ</math> |
||
<!-- # [[Гексагональная сингония|Гексагональная]] — имеет одну ось 6-го порядка;--> |
<!-- # [[Гексагональная сингония|Гексагональная]] — имеет одну ось 6-го порядка;--> |
||
** [[Тригональная|Тригональная]]: <math>~a=b=c</math>, <math>~\alpha = \beta = \gamma \ne 90^\circ</math> |
|||
<!-- # [[Тригональная сингония|Тригональная]] — имеет одну ось 3-го порядка;--> |
|||
* Высшая категория (все трансляции равны между собой) |
* Высшая категория (все трансляции равны между собой) |
||
Версия от 23:10, 11 января 2010
Синго́ния (от греч. σύν, «согласно, вместе», и γωνία, «угол» — дословно «сходноугольность») — одно из подразделений кристаллов по признаку формы их элементарной ячейки. В основном применяется в кристаллографии для категоризации кристаллов, но представление о сингонии само по себе является одной из тем трехмерной евклидовой геометрии.
Категоризация
Элементарная ячейка кристалла строится на трёх некомпланарных векторах , называемых трансляциями. В зависимости от соотношения между длинами этих трансляций и углами между ними выделяют шесть различных сингоний, которые распадаются на три категории в зависимости от числа равных длин трансляций:
- Низшая категория (все трансляции не равны друг другу)
- Триклинная: ,
- Моноклинная: ,
- Ромбическая (или орторомбическая): ,
- Средняя категория (две трансляции из трёх равны между собой)
- Тетрагональная: ,
- Гексагональная: ,
- Высшая категория (все трансляции равны между собой)
- Кубическая: ,
В отечественной специальной литературе существует путаница двух понятий — сингонии (crystal family) и кристаллической системы (crystal system), которые часто используются как синонимы. Разбиение на кристаллические системы выполняется в зависимости от набора элементов симметрии, описывающих кристалл. Такое деление приводит к семи кристаллическим системам, две из которых — тригональная (с одной осью 3-го порядка) и гексагональная (с одной осью 6-го порядка) — имеют одинаковую по форме элементарную ячейку и поэтому относятся к одной, гексагональной, сингонии.
Имеется ряд пространственных групп на каждую сингонию 2, 13, 59, 68, 25, 27 и 36 соответственно, всего — 230 групп. Они представлены ниже в таблице:
| Сингония | Число точечных групп | Число решёток Бравэ | Число пространственных групп |
| Триклинная | 2 | 1 | 2 |
| Моноклинная | 3 | 2 | 13 |
| Ромбическая (орторомбическая) |
3 | 4 | 59 |
| Тетрагональная | 7 | 2 | 68 |
| Тригональная (ромбоэдрическая) | 5 | 1 | 25 |
| Гексагональная | 7 | 1 | 27 |
| Кубическая | 5 | 3 | 36 |
| Всего | 32 | 14 | 230 |
Обзор точечных групп сингоний
| сингония | точечная группа / класс симметрии | Символ Шёнфлиса | Международный символ | orbifold(?) | Тип |
|---|---|---|---|---|---|
| триклинная | триклино-педиальный (моноэдрический) | C1 | 11 | энантиоморфный полярный | |
| триклинно-пинакоидальный | Ci | 1x | центросимметричный | ||
| моноклинная | моноклино-сфеноидальный (диэдрический осевой) | C2 | 22 | энантиоморфный полярный | |
| моноклинно-доматический | Cs | 1* | полярный | ||
| моноклинно-призматический | C2h | 2* | центросимметричный | ||
| Ромбическая орторомбическая |
ромбо-сфеноидальный (ромбо-тетраэдрический) | D2 | 222 | энантиоморфный | |
| ромбо-пирамидальный | C2v | *22 | полярный | ||
| ромбо-дипирамидальный (бипирамидальный) | D2h | *222 | центросимметричный | ||
| Тетрагональная | тетрагонально-пирамидальный | C4 | 44 | энантиоморфный полярный | |
| тетрагонально-дисфеноидальный (тетраэдрический) | S4 | 2x | |||
| тетрагонально-дипирамидальный | C4h | 4* | центросимметричный | ||
| тетрагонально-трапециоэдрический | D4 | 422 | энантиоморфный | ||
| дитетрагонально-пирамидальный | C4v | *44 | полярный | ||
| тетрагонально-скаленоэдрический | D2d | or | 2*2 | ||
| дитетрагонально-дипирамидальный | D4h | *422 | центросимметричный | ||
| Тригональная (ромбоэдрическая) |
тригонально-пирамидальный | C3 | 33 | энантиоморфный полярный | |
| ромбоэдрический | S6 (C3i) | 3x | центросимметричный | ||
| тригонально-трапецоэдрический | D3 | или или | 322 | энантиоморфный | |
| дитригонально-пирамидальный | C3v | or или | *33 | полярный | |
| дитригонально-скаленоэдрический | D3d | или или | 2*3 | центросимметричный | |
| Гексагональная | гексагонально-пирамидальный | C6 | 66 | энантиоморфный полярный | |
| тригонально-дипирамидальный | C3h | 3* | |||
| гексагонально-дипирамидальный | C6h | 6* | центросимметричный | ||
| гексагонально-трапецоэдрический | D6 | 622 | энантиоморфный | ||
| дигексагонально-пирамидальный | C6v | *66 | полярный | ||
| дитригонально-дипирамидальный | D3h | или | *322 | ||
| дигексагонально-дипирамидальный | D6h | *622 | центросимметричный | ||
| Кубическая | тетартоидальный (тритетраэдрический) | T | 332 | энантиоморфный | |
| диплоидальный (дидодекаэдрический) | Th | 3*2 | центросимметричный | ||
| гироидальный (триоктаэдрический) | O | 432 | энантиоморфный | ||
| тетраэдрический (гексатетраэдрический) | Td | *332 | |||
| гексоктаэдрический | Oh | *432 | центросимметричный |
Классификация решеток
| Сингония | Решётки Бравэ | |||
| Триклинная (ромбоэдр) |
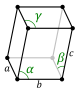
| |||
| Моноклинная (правильная призма с параллелограммом в основании (изображен сверху); |
простая | базоцентрированная | ||
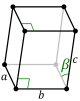
|

| |||
| Ромбическая (параллелепипед) |
простая | базоцентрированная | объёмноцентрированная | гранецентрированная |
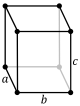
|

|
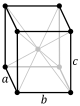
|

| |
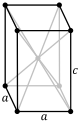
| Тетрагональная (прямой параллелепипед) |
простая | объёмноцентрированная | ||

|
| |||
| Тригональная (ромбоэдрическая) (равносторонний ромбоэдр) |

| |||
| Гексагональная (призма с основанием правильного центрированного шестиугольника) |

| |||
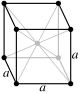
| Кубическая (правильный куб) |
простая | объёмноцентрированная | гранецентрированная | |

|
|

| ||
















































