Задача о максимальном потоке: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
Urod (обсуждение | вклад) |
Urod (обсуждение | вклад) Нет описания правки |
||
| Строка 131: | Строка 131: | ||
|страницы = 1296 |
|страницы = 1296 |
||
|isbn = 0-07-013151-1 |
|isbn = 0-07-013151-1 |
||
}}, глава 26 |
}}, глава 26. Максимальный поток. |
||
==Сноски== |
==Сноски== |
||
| Строка 195: | Строка 195: | ||
| issue = 3 |
| issue = 3 |
||
}} |
}} |
||
# {{книга |
|||
# {{cite book | author = [[Thomas H. Cormen]], [[Charles E. Leiserson]], [[Ronald L. Rivest]], and [[Clifford Stein]] | title=[[Introduction to Algorithms]], Second Edition | chapter = 26. Maximum Flow | year = 2001 | publisher = MIT Press and McGraw-Hill | isbn = 0-262-03293-7 | pages=643–668}} |
|||
|автор = Томас Х. Кормен и др. |
|||
|заглавие = Алгоритмы: построение и анализ |
|||
|оригинал = INTRODUCTION TO ALGORITHMS |
|||
|ссылка = |
|||
|издание = 2-е изд |
|||
|место = М. |
|||
|издательство = [[Вильямс (издательство)|«Вильямс»]] |
|||
|год = 2006 |
|||
|страницы = 1296 |
|||
|isbn = 0-07-013151-1 |
|||
}}, глава 26. Максимальный поток. |
|||
# {{cite book | author = Eugene Lawler | authorlink = Eugene Lawler | title = Combinatorial Optimization: Networks and Matroids | chapter = 4. Network Flows | year = 2001 | publisher = Dover | isbn = 0486414531 | pages = 109–177}} |
# {{cite book | author = Eugene Lawler | authorlink = Eugene Lawler | title = Combinatorial Optimization: Networks and Matroids | chapter = 4. Network Flows | year = 2001 | publisher = Dover | isbn = 0486414531 | pages = 109–177}} |
||
Версия от 15:21, 28 октября 2010
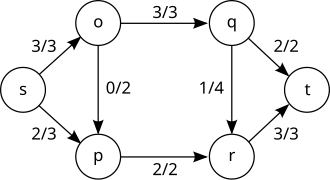
В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сумма потоков из источника, или, что то же самое, сумма потоков в сток максимальна.
Задача о максимальном потоке является частным случаем более трудных задач, как например задача о циркуляции.
История
После вступления США во Вторую мировую войну в 1941 году, математик Джордж Бернард Данциг поступил на работу в отдел статистического управления Военно-воздушные силы США в Вашингтоне. С 1941 по 1946 годы он возглавлял подразделение анализа военных действий (Combat Analysis Branch), где работал над различными математическими проблемами.[1][2] Впоследствии, используя работу Данцига, задача о максимальном потоке была впервые решена в ходе подготовки воздушного моста во время блокады Западного Берлина, происходившей в 1948-1949 году.[3][4][5]
В 1951 году Джордж Данциг впервые сформулировал задачу в общем виде.[6]
В 1955 году, Шаблон:Translation2 и Шаблон:Translation2 впервые построили алгоритм, специально предназначенный для решения этой задачи. Их алгоритм получил название алгоритм Форда-Фалкерсона.[7][8]
В дальнейшем решение задачи много раз улучшалось.
В 2010 году исследователи Джонатан Кёлнер (Jonathan Kelner) и Александр Мэдри (Aleksander Mądry) из МТИ вместе со своими коллегами Дэниелем Спилманом (en:Daniel Spielman) из Йельского уноверситета и Шень-Хуа Тенем (en:Shang-Hua Teng) из Южно-Калифорнийского университета продемонстрировали очередное улучшение алгоритма, впервые за 10 лет.[3][9][10]
Определение
Дана транспортная сеть с источником , стоком и пропускными способностями .
- Величиной потока (value of flow) называется сумма потоков из источника . В статье «Транспортная сеть» доказано, что она равна сумме потоков в сток .
Задача о максимальном потоке заключается в нахождении потока такого, что величина потока максимальна.
Решения
Следующая таблица перечисляет некоторые алгоритмы решения задачи.
| Метод | Сложность | Описание |
|---|---|---|
| Линейное программирование | Зависит от конкретного алгоритма. Для симплекс-метода экспоненциальна. |
Представить задачу о максимальном потоке как задачу линейного программирования. Переменными являются потоки по рёбрам, а ограничениями - сохранение потока и ограничение пропускной способности. |
| Алгоритм Форда-Фалкерсона | Зависит от алгоритма поиска увеличивающего пути. Требует O(max| f |) таких поисков. |
Найти любой увеличивающий путь. Увеличить поток по всем его рёбрам на минимальную из их остаточных пропускных способностей. Повторять, пока увеличивающий путь есть. Алгоритм работает только для целых пропускных способностей. В противном случае, он может работать бесконечно долго, не сходясь к правильному ответу. |
| Алгоритм Эдмондса-Карпа | O(VE2) | Выполняем алгоритм Форда-Фалкерсона, каждый раз выбирая кратчайший увеличивающий путь (находится поиском в ширину). |
| Алгоритм Диница | O(V2E) для единичных пропускных способностей с использованием динамических дереьев Слетора и Тарьяна[11] |
Усовершенствование алгоритма Эдмондса-Карпа (но хронологически был найден раньше). На каждой итерации, используя поиск в ширину, определяем расстояния от источника до всех вершин в остаточной сети. Строим граф, содержащий только такие рёбра остаточной сети, на которых это расстояние растёт на 1. Исключаем из графа все тупиковые вершины с инцидентными им рёбрами, пока все вершины не станут нетупиковыми. (Тупиковой называется вершина, кроме источника и стока, в которую не входит ни одно ребро или из которой не исходит ни одного ребра.) На получившемся графе отыскиваем кратчайший увеличивающий путь (им будет любой путь из s в t). Исключаем из остаточной сети ребро с минимальной пропускной способностью, снова исключаем тупиковые вершины, и так пока увеличивающий путь есть. |
| Алгоритм проталкивания предпотока | O(V2E) | Вместо потока оперирует с предпотоком. Отличие в том, что для любой вершины u, кроме источника и стока, сумма входящих в неё потоков для потока должна быть строго нулевой (условие сохранения потока), а для предпотока — неотрицательной. Эта сумма называется избыточным потоком в вершину, а вершина с положительным избыточным потоком называется переполненной. Кроме того, для каждой вершины алгоритм сохраняет дополнительную характеристику, высоту, являющуюся целым неотрицательным числом. Алгоритм использует две операции: проталкивание, когда поток по ребру, идущему из более высокой в более низкую вершину, увеличивается на максимально возможную величину, и подъём, когда переполненная вершина, проталкивание из которой невозможно из-за недостаточной высоты, поднимается. Проталкивание возможно, когда ребро принадлежит остаточной сети, ведёт из более высокой вершины в более низкую, и исходная вершина переполнена. Подъём возможен, когда поднимаемая вершина переполнена, но ни одна из вершин, в которые из неё ведут рёбра остаточной сети, не ниже её. Он совершается до высоты на 1 большей, чем минимальная из высот этих вершин. Изначально высота источника V, по всем рёбрам, исходящим из источника, течёт максимально возможный поток, а остальные высоты и потоки нулевые. Операци проталкивания и подъёма выполняются до тех пор, пока это возможно. |
| Алгоритм "поднять в начало" | O(V3) O(VE log(V2/E)) с использованием динамических деревьев |
Вариант предыдущего алгоритма, специальным образом определяющий порядок операций проталкивания и подъёма. |
| Алгоритм двоичного блокирующего потока [1] |
Для более подробного списка, см. [2].
Теорема о целом потоке
Если пропускные способности целые, максимальная величина потока тоже целая.
Теорема следует, например, из теоремы Форда—Фалкерсона.
Обобщения, сводящиеся к исходной задаче
Некоторые обобщения задачи о максимальном потоке легко сводятся к исходной задаче.
Произвольное число источников и/или стоков
Если источников больше одного, добавляем новую вершину S, которую делаем единственным источником. Добавляем рёбра с бесконечной пропускной способностью от S к каждому из старых источников.
Аналогично, если стоков больше одного, добавляем новую вершину T, которую делаем единственным стоком. Добавляем рёбра с бесконечной пропускной способностью от каждого из старых стоков к T.
Неориентированные рёбра
Каждое неориентированное ребро (u, v) заменяем на пару ориентированных рёбер (u, v) и (v, u).
Ограничение пропускной способности вершин
Каждую вершину v с ограниченной пропускной способностью расщепляем на две вершины vin и vout. Все рёбра, до расщепления входящие в v, теперь входят в vin. Все рёбра, до расщепления исходящие из v, теперь исходят из vout. Добавляем ребро (vin,vout) с пропускной способностью .
См. также
Литература
- Schrijver, Alexander, "On the history of the transportation and maximum flow problems", Mathematical Programming 91 (2002) 437-445
- Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1., глава 26. Максимальный поток.
Сноски
- ↑ Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. George Dantzig (англ.) — биография в архиве MacTutor.
- ↑ Cottle, Richard; Johnson, Ellis; Wets, Roger, "George B. Dantzig (1914–2005)", Notices of the American Mathematical Society, v.54, no.3, March 2007. Cf. p.348
- ↑ 1 2 Hardesty, Larry, "First improvement of fundamental algorithm in 10 years", MIT News Office, September 27, 2010
- ↑ Borndörfer, Ralf; Grötschel, Martin; Löbel, Andreas, "Alcuin's Transportation Problems and Integer Programing", Konrad-Zuse-Zentrum für Informationstechnik, Berlin, Germany, November 1995. Cf. p.3
- ↑ Powell, Stewart M., "The Berlin Airlift", Air Force Magazine, June 1998.
- ↑ Dantzig, G.B., "Application of the Simplex Method to a Transportation Problem", in T.C. Koopman (ed.): Activity Analysis and Production and Allocation, New York, (1951) 359-373.
- ↑ Ford, L.R., Jr.; Fulkerson, D.R., "Maximal Flow through a Network", Canadian Journal of Mathematics (1956), pp.399-404.
- ↑ Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
- ↑ Kelner, Jonathan, "Electrical Flows, Laplacian Systems and Faster Approximation of Maximum Flow in Undirected Graphs", talk at CSAIL, MIT, Tuesday, September 28 2010
- ↑ [http://math.mit.edu/~kelner/Publications/Docs/maxFlow.pdf Electrical Flows, Laplacian Systems, and Faster Approximation of Maximum Flow in Undirected Graphs], by Paul Cristiano et al., October 19, 2010.
- ↑ Алгоритм Диница
Примечания
- ↑ Andrew V. Goldberg and S. Rao [in английский] (1998). "Beyond the flow decomposition barrier". J. Assoc. Comput. Mach. 45: 753—782. doi:10.1145/290179.290181.
- ↑ Andrew V. Goldberg and Robert E. Tarjan [in английский] (1988). "A new approach to the maximum-flow problem". Journal of the ACM. 35 (4). ACM Press: 921—940. doi:10.1145/48014.61051. ISSN 0004-5411.
{{cite journal}}: Неизвестный параметр|address=игнорируется (|location=предлагается) (справка) - ↑ Joseph Cheriyan and Kurt Mehlhorn [in английский] (1999). "An analysis of the highest-level selection rule in the preflow-push max-flow algorithm". Information Processing Letters. 69 (5): 239—242. doi:10.1016/S0020-0190(99)00019-8.
- ↑ Daniel D. Sleator and Robert E. Tarjan [in английский] (1983). "A data structure for dynamic trees" (PDF). Journal of Computer and System Sciences. 26 (3): 362—391. doi:10.1016/0022-0000(83)90006-5. ISSN 0022-0000.
- ↑ Daniel D. Sleator and Robert E. Tarjan [in английский] (1985). "Self-adjusting binary search trees" (PDF). Journal of the ACM. 32 (3). ACM Press: 652—686. doi:10.1145/3828.3835. ISSN 0004-5411.
{{cite journal}}: Неизвестный параметр|address=игнорируется (|location=предлагается) (справка) - Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1., глава 26. Максимальный поток.
- Eugene Lawler. 4. Network Flows // Combinatorial Optimization: Networks and Matroids. — Dover, 2001. — P. 109–177. — ISBN 0486414531.









