Ломаная: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
X7q (обсуждение | вклад) м откат правок 109.172.31.64 (обс) к версии 89.110.59.239 |
|||
| Строка 6: | Строка 6: | ||
Ло́маной (ломаной линией) A<sub>1</sub>A<sub>2</sub>...A<sub>n</sub> называется фигура, которая состоит из отрезков A<sub>1</sub>A<sub>2</sub>, A<sub>2</sub>A<sub>3</sub>, ..., A<sub>n-1</sub>A<sub>n</sub>. Точки A<sub>1</sub>, A<sub>2</sub>, ..., A<sub>n</sub> называются вершинами ломаной, а отрезки A<sub>1</sub>A<sub>2</sub>, A<sub>2</sub>A<sub>3</sub>, ..., A<sub>n-1</sub>A<sub>n</sub> − звеньями ломаной. При этом требуется, чтобы для любого k ∈ {2, 3, ..., n-1} отрезки A<sub>k-1</sub>A<sub>k</sub> и A<sub>k</sub>A<sub>k+1</sub> не лежали на одной прямой. Это требование накладывается и на отрезки A<sub>1</sub>A<sub>2</sub> и A<sub>n-1</sub>A<sub>n</sub> при совпадении A<sub>1</sub> и A<sub>n</sub>. |
Ло́маной (ломаной линией) A<sub>1</sub>A<sub>2</sub>...A<sub>n</sub> называется фигура, которая состоит из отрезков A<sub>1</sub>A<sub>2</sub>, A<sub>2</sub>A<sub>3</sub>, ..., A<sub>n-1</sub>A<sub>n</sub>. Точки A<sub>1</sub>, A<sub>2</sub>, ..., A<sub>n</sub> называются вершинами ломаной, а отрезки A<sub>1</sub>A<sub>2</sub>, A<sub>2</sub>A<sub>3</sub>, ..., A<sub>n-1</sub>A<sub>n</sub> − звеньями ломаной. При этом требуется, чтобы для любого k ∈ {2, 3, ..., n-1} отрезки A<sub>k-1</sub>A<sub>k</sub> и A<sub>k</sub>A<sub>k+1</sub> не лежали на одной прямой. Это требование накладывается и на отрезки A<sub>1</sub>A<sub>2</sub> и A<sub>n-1</sub>A<sub>n</sub> при совпадении A<sub>1</sub> и A<sub>n</sub>. |
||
'''Замкнутая ломаная линия - это...''' - закончите предложение. |
|||
== Типы ломанных == |
== Типы ломанных == |
||
Версия от 13:46, 3 апреля 2011

Ло́маная (ломаная линия) — геометрическая фигура, состоящая из отрезков, последовательно соединенных своими концами.
Определение
Ло́маной (ломаной линией) A1A2...An называется фигура, которая состоит из отрезков A1A2, A2A3, ..., An-1An. Точки A1, A2, ..., An называются вершинами ломаной, а отрезки A1A2, A2A3, ..., An-1An − звеньями ломаной. При этом требуется, чтобы для любого k ∈ {2, 3, ..., n-1} отрезки Ak-1Ak и AkAk+1 не лежали на одной прямой. Это требование накладывается и на отрезки A1A2 и An-1An при совпадении A1 и An.
Типы ломанных
Ломаная может иметь самопересечения:
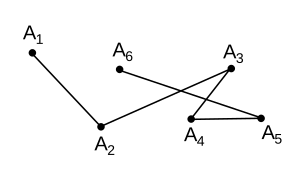
Если первая и последняя точки ломаной совпадают, то такая ломаная называется замкнутой.
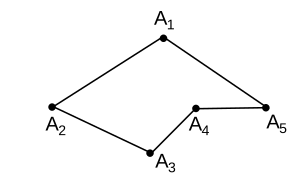
Изображённую здесь ломаную следует называть A1A2A3A4A5A1. Замкнутую ломаную можно также называть многоугольником. В этом случае изображённая фигура будет называться "многоугольник"
A1A2A3A4A5"