Квадратура круга

Круг и квадрат одинаковой площади

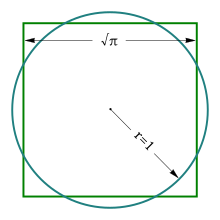
Квадрату́ра кру́га — задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу.

Наряду с трисекцией угла и удвоением куба, является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.

Неразрешимость

Если принять за единицу измерения радиус круга и обозначить x длину стороны искомого квадрата, то задача сводится к решению уравнения: $x^{2}=\pi$, откуда: $x={\sqrt {\pi }}$. Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины $\pi$. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа $\pi$, которая была доказана в 1882 году Линдеманом.

Однако эту неразрешимость следует понимать, как неразрешимость при использовании только циркуля и линейки. Задача о квадратуре круга становится разрешимой, если, кроме циркуля и линейки, использовать другие средства (например, квадратрису). Простейший механический способ предложил Леонардо да Винчи. Изготовим круговой цилиндр с радиусом основания $R$ и высотой ${\frac {R}{2}}$, намажем его чернилами и прокатим по плоскости. За один полный оборот цилиндр отпечатает на плоскости прямоугольник площадью $\pi R^{2}$. Располагая таким прямоугольником, уже несложно построить равновеликий ему квадрат.

Приближённое решение

Диагональ искомого квадрата приближённо равна 2,5 радиусам круга. Построив квадрат со стороной указанной длины и взяв половину его диагонали, получим сторону искомого приближённого квадрата.

Метафора «Квадратура круга»

Математическое доказательство невозможности квадратуры круга не мешало многим энтузиастам тратить годы на решение этой проблемы. Тщетность исследований по решению задачи квадратуры круга перенесла этот оборот во многие другие области, где он попросту обозначает безнадежное, бессмысленное или тщетное предприятие. См. также Вечный двигатель

См. также

• Квадратриса
• Построение с помощью циркуля и линейки
• Трисекция угла
• Удвоение куба
• Квадратура круга Тарского

Литература

• Манин Ю. И. О разрешимости задач на построение с помощью циркуля и линейки. Энциклопедия элементарной математики. Книга четвёртая (геометрия), М., Физматгиз, 1963. — 568 с.
• Перельман Я. И. Квадратура круга. Л.: Дом занимательной науки, 1941. Текст в формате djv/zip - ссылка мертвая.
• Прасолов В. В.. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. М.: Наука, 1992. 80 с. Серия «Популярные лекции по математике», выпуск 62.
• Рудио Ф. О квадратуре, круга (Архимед, Гюйгенс, Ламберт, Лежандр), с приложением истории вопроса. Издание третье. М.-Л.: Огиз, 1936. Серия: Классики естествознания.
• Хал Хеллман. Великие противостояния в науке. Десять самых захватывающих диспутов - Глава 2. Валлис против Гоббса: Квадратура круга = Great Feuds in Science: Ten of the Liveliest Disputes Ever. — М.: «Диалектика», 2007. — 320 с. — ISBN 0-471-35066-4.
• Щетников А. И. Как были найдены некоторые решения трёх классических задач древности? Математическое образование, № 4 (48), 2008, с. 3–15.