Двумерное пространство: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
EmausBot (обсуждение | вклад) м r2.7.2+) (бот изменил: ar:الفضاء ثنائي الأبعاد на ar:فضاء ثنائي الأبعاد |
EmausBot (обсуждение | вклад) м Перемещение 24 интервики-ссылок в Викиданные (d:Q222032) |
||
| Строка 115: | Строка 115: | ||
[[Категория:Геометрия]] |
[[Категория:Геометрия]] |
||
[[als:Zweidimensional]] |
|||
[[ar:فضاء ثنائي الأبعاد]] |
|||
[[ca:Espai bidimensional]] |
|||
[[cs:2D]] |
|||
[[da:2-D]] |
|||
[[de:2D]] |
|||
[[en:Two-dimensional space]] |
|||
[[es:Bidimensional]] |
|||
[[fa:فضای دوبعدی]] |
|||
[[fi:Kaksiulotteisuus]] |
|||
[[it:Bidimensionalità]] |
|||
[[ja:2次元]] |
|||
[[ko:2차원]] |
|||
[[nl:Tweedimensionaal]] |
|||
[[no:2D]] |
|||
[[pt:Espaço bidimensional]] |
|||
[[ro:2D]] |
|||
[[simple:2D]] |
|||
[[sk:2D]] |
|||
[[sv:2D]] |
|||
[[ta:ஈரளவு வெளி]] |
|||
[[tr:İki boyutlu uzay]] |
|||
[[vec:2D]] |
|||
[[zh:二维空间]] |
|||
Версия от 21:33, 13 марта 2013
Двуме́рное простра́нство (иногда говорят двухме́рное пространство) — геометрическая модель плоской проекции физического мира, в котором мы живём. Двумерным пространством считается n-мерное пространство, где n=2.
Примером двумерного пространства является плоскость. Точки данного пространства возможно задать всего двумя числами. Например, любую точку можно задать парой чисел: (x, y). Плоские объекты характеризуются не только длиной, но и шириной[1].
Геометрия двумерного пространства
Многогранники
В двумерном пространстве существует бесконечно много правильных многогранников: правильные многоугольники. Примеры последних приведены ниже:
Символ {p} (символ Шлефли) обозначает правильный p-угольник.
| Название | Треугольник (2-симплекс) |
Квадрат (2-куб) |
Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | |
|---|---|---|---|---|---|---|---|
| Символ Шлефли | {3} | {4} | {5} | {6} | {7} | {8} | |
| Вид | 
|

|

|

|

|

| |
| Название | Девятиугольник | Десятиугольник | 11-угольник | 12-угольник | 13-угольник | 14-уольник | |
| Символ Шлефли | {9} | {10} | {11} | {12} | {13} | {14} | |
| Вид | 
|

|

|

|

|

| |
| Название | 15-угольник | 16-угольник | 17-угольник | 18-угольник | 19-угольник | 20-угольник | ...n-угольник |
| Символ Шлефли | {15} | {16} | {17} | {18} | {19} | {20} | {n} |
| Вид | 
|

|

|

|

|
|
Гиперсфера
Гиперсферой в двумерном пространстве является окружность, которую иногда называют 1-сфера, потому что её поверхность является одномерной. Площадь части плоскости, заключённой внутри гиперсферы (площадь круга) равна:
- ,
где — радиус окружности.
Системы координат в двумерном пространстве
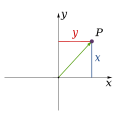
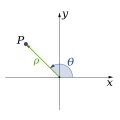
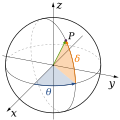
Наиболее распространённые координатные системы — прямоугольная (Декартова) система координат, полярная система координат и географическая координатная система.
Примечания
См. также