Salsa20: различия между версиями
| [отпатрулированная версия] | [непроверенная версия] |
м →ChaCha: заменил в формуле "\lll" на "\lll=" .. хотя по-моему всё равно кривовато выглядит |
|||
| Строка 102: | Строка 102: | ||
Где <math>c[i]=m[i] \oplus Salsa20_k(v,\mathcal {b}\underline{i/64}\mathcal {c})[i\mod 64]</math> |
Где <math>c[i]=m[i] \oplus Salsa20_k(v,\mathcal {b}\underline{i/64}\mathcal {c})[i\mod 64]</math> |
||
== Производительность == |
|||
== Скоростные особенности == |
|||
| ⚫ | |||
| ⚫ | |||
Другим скоростным преимуществом является то, что алгоритм практически не имеет накладных вычислений для запуска цикла шифрования. |
|||
Алгоритм практически не имеет накладных вычислений, необходимых для запуска цикла шифрования. Это так же относится к смене ключа. Многие шифросистемы рассчитывают на предварительные вычисления, результаты которых должны храниться в [[Кэш процессора|кэше]] первого уровня (L1) [[процессор]]а. Так как они зависят от ключа, вычисления придётся проводить заново. В Salsa20 же достаточно просто загрузить ключ в память. |
|||
== Варианты Salsa20/8 и Salsa20/12 == |
== Варианты Salsa20/8 и Salsa20/12 == |
||
Версия от 18:29, 25 марта 2015
Salsa20 — система поточного шифрования разработанная Daniel J. Bernstein. Алгоритм был представлен на конкурсе eSTREAM, целью которого было создание европейских стандартов для поточных систем шифрования. Алгоритм стал победителем конкурса в первом профиле (поточные шифры для программного применения с большой пропускной способностью).
Salsa20 основана на операциях 32-битного суммирования, побитового сложения (XOR) и операции сдвига. Алгоритм использует хеш-функцию с 20-ю циклами. Основные её преобразования напоминают алгоритм AES.
Описание алгоритма
Понятия
Словом далее будем называть элемент множества {0,1,…,232−1} и записывать в шестнадцатеричном виде с префиксом 0х.
Операцию сложения двух слов по модулю 232 будем обозначать знаком «».
Исключающее или (побитовое суммирование) будем обозначать символом «»
-битовый циклический левый сдвиг слова будем обозначать . Если представить как , тогда
Функции, используемые в алгоритме

quarterround(y)
Основным блоком системы является преобразование над 4-мя словами. Из него строятся далее описанные более общие преобразования. Его суть заключается в том, что для каждого слова мы складываем два предыдущих, сдвигаем сумму на определенное количество бит и побитово суммируем результат с выбранным словом. Последующие операции производятся с новыми значениями слов.
Допустим, что — последовательность 4-х слов тогда функция где
Например:
quarterround(0x00000001; 0x00000000; 0x00000000; 0x00000000)
= (0x08008145; 0x00000080; 0x00010200; 0x20500000)
Можно рассматривать эту функцию как преобразования слов y1, y2, y3 и y4. Каждое из таких преобразований обратимо, как и функция в целом.
rowround(y)
В этом преобразовании мы берем 16 слов. Представим их в виде матрицы 4х4. Берем каждый ряд этой матрицы и преобразуем слова этой матрицы функцией . Слова из строки берутся по порядку, начиная с i-го для i-й строки, где i={0,1,2,3}.
Пусть — последовательность 16 слов, тогда — также последовательность 16 слов где
columnround(y)
Здесь мы берём столбцы такой же матрицы. Преобразуем их функцией , по аналогии подставляя в неё значения, начиная с j-го для j-го столбца, где j={0,1,2,3}.
Функция columnround(y)=(z) тоже оперирует последовательностью 16-и слов так, что
doubleround(y)
Функция doubleround(y) является последовательным применением функций columnround а затем rowround: doubleround(y) = rowround(columnround(y))
Salsa20()
Данный алгоритм использует запись слова начинающуюся с младшего байта. Для этого здесь введено преобразование
Пусть — 4-байтовая последовательность, тогда — слово, такое что
Итоговое преобразование — это побитовое суммирование исходной последовательности и результата 20 раундов чередующихся преобразований столбцов и строк.
Где
- …
x[i] — байты x, а xj — слова, используемые в описанных выше функциях.
Если
,
тогда Salsa20(x) является последовательностью результатов
Расширение ключа для Salsa20
Расширение преобразует 32-байтный или 16-байтный ключ k и 16-байтный номер n в 64-байтную последовательность .
Для расширения k используются константы
для 32-битного k и
для 16-битного k.
Это записи «expand 32-byte k» и «expand 16-byte k» ASCII-коде.
Пусть у k0,k1,n — 16-байтовые последовательности, тогда
.
Если у нас только одна 16-байтовая последовательность k то
Функция шифрования Salsa20
Шифром -байтной последовательности , для будет
— уникальный 8-байтовый номер(nonce).
Шифротекст будет размером в байт, так же как и исходный текст.
Salsa20k(v) — последовательность в 270 байт.
Где — уникальная последовательность в 8 байт такая что Соответственно
Где
Производительность
Благодаря тому, что преобразования каждого столбца и каждой строки не зависят друг от друга, вычисления, необходимые для шифрования, легко распараллеливаются. Это даёт существенный выигрыш в скорости для большинства современных платформ.
Алгоритм практически не имеет накладных вычислений, необходимых для запуска цикла шифрования. Это так же относится к смене ключа. Многие шифросистемы рассчитывают на предварительные вычисления, результаты которых должны храниться в кэше первого уровня (L1) процессора. Так как они зависят от ключа, вычисления придётся проводить заново. В Salsa20 же достаточно просто загрузить ключ в память.
Варианты Salsa20/8 и Salsa20/12
Salsa20/8 и Salsa20/12 это шифросистемы, использующие тот же механизм что и Salsa20, но с 8-ю и 12-ю раундами шифрования соответственно вместо 20 оригинальных. Salsa20 был сделан с большим запасом стойкости. Тогда как Salsa20/8 показывает хорошие результаты в быстродействии, обгоняя в большинстве случаев многие другие шифросистемы, в том числе AES и RC4[1]
Криптоанализ
В 2005 году Paul Crowley объявил об атаке на Salsa20/5 с расчетной сложностью по времени 2165. Эта и последующие атаки основаны на усеченном дифференциальном криптоанализе(truncated differential cryptanalysis). За этот криптоанализ он получил награду в 1000$ от автора Salsa20.
B 2006, Fischer, Meier, Berbain, Biasse, и Robshaw сообщили об атаке на Salsa/6 со сложностью 2117, и об атаке со связанными ключами на Salsa20/7 со сложностью 2217
B 2008 году Aumasson, Fischer, Khazaei, Meier и Rechberger сообщили об атаке на Salsa20/7 со сложностью 2153 и о первой атаке на Salsa20/8 со сложностью 2251.
Пока что не было публичных сообщений об атаках на Salsa20/12 и полную Salsa20/20.
ChaCha
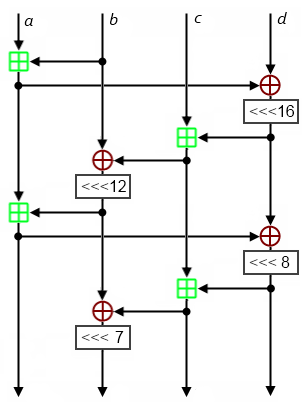
В 2008 году Daniel Bernstein опубликовал родственное семейство поточных шифров под названием ChaCha, целью которого было улучшение перемешивания данных за один раунд и, предположительно, улучшение криптостойкости при той же, или даже немного большей скорости.[2]
Основной блок системы здесь работает иначе. Теперь каждая операция изменяет одно из слов. Изменения происходят циклически «в обратную сторону», начиная с 0-го слова. Чередуются операции сложения и побитовой суммы вместе со сдвигом. складывается слово с предыдущим.
Функция quarterround(a, b, c, d), где a, b, c, d-слова, в ChaCha выглядит следующим образом
Здесь используются те же самые арифметические операции, но каждое слово изменяется два раза за преобразование вместо одного.
































![{\displaystyle ~x=(x[0],x[1],...,x[63]),}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/6b7cd9506cef4eb72a99fb2007f7e3776c13e893)
![{\displaystyle ~x_{0}=littleendian(x[0],x[1],x[2],x[3]),}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/f830b9ca3fc07bdb9eb82710f2cffbb144dda4c0)
![{\displaystyle ~x_{1}=littleendian(x[4],x[5],x[6],x[7]),}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/3cf823606c0fdb987059527e7b36865f7ffd83dd)
![{\displaystyle ~x_{15}=littleendian(x[60],x[61],x[62],x[63]).}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/680c09053168889333d227cef7b062f209ad11c4)
















![{\displaystyle Salsa20_{k}(v)\oplus (m[0],m[1],..,m[l-1])=(c[0],c[1],...,c[l-1])}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/9ac51a8685f904b27bc8f034aaf60bbbe0c2ffab)
![{\displaystyle c[i]=m[i]\oplus Salsa20_{k}(v,{\mathcal {b}}{\underline {i/64}}{\mathcal {c}})[i\mod 64]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/5943e1e6bdefb0f9a2d9522e38a96f11ce0cb369)



