Классификатор подобъектов

В теории категорий, классификатор подобъектов — специальный объект Ω категории; интуитивно, подобъекты X соответствуют морфизмам из X в Ω. Способ, которым он «классифицирует» объекты можно описать как присвоение некоторым элементам X значения «истина».

Вводный пример

В категории множеств классификатор подобъектов — множество Ω = {0,1}, морфизмы в него соответствуют характеристическим функциям. Если χ_A — некоторая характеристическая функция на множестве S, следующая диаграмма является декартовым квадратом:

Здесь true: {0} → {0, 1} — каноническое отображение, отправляющее 0 в 1.

Определение

В общем случае можно рассмотреть произвольную категорию C, имеющую терминальный объект, который мы будем обозначать 1. Объект Ω категории C — классификатор подобъектов C, если существует морфизм

1 → Ω

со следующим универсальным свойством:

для любого мономорфизма j: U → X существует единственный морфизм χ _j: X → Ω, такой что слеюующая коммутативная диаграмма

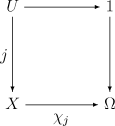
является диаграммой декартова произведения, то есть U — предел диаграммы

Морфизм χ _j называется классифицирующим морфизмом для подобъекта, представленного мономорфизмом j.

См. также

• Топос (математика)

Примечания

• Artin Michael, Alexander Grothendieck, Jean-Louis Verdier. Séminaire de Géometrie Algébrique IV. — Springer-Verlag, 1964.
• Johnstone, Peter. Topos Theory. — Academic Press, 1977. — ISBN 0-12-387850-0.
• Mac Lane, Saunders. Sheaves in Geometry and Logic: a First Introduction to Topos Theory. — Springer-Verlag, 1992. — ISBN 0-387-97710-4.
• Topos-physics: An explanation of Topos theory and its implementation in Physics Topos-physics, Where Geometry meets Dynamics
• Голдблатт, Р. Топосы. Категорный анализ логики, — М.: Мир, 1983. — 487 с.
• С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с — ISBN 5-9221-0400-4.