Кривая погони

Кривая погони при различных параметрах

Простая кривая погони

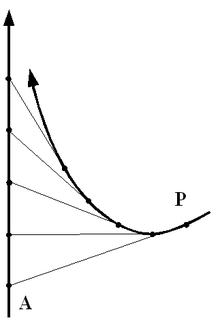
Кривая погони — кривая, представляющая собой решение задачи о «погоне», которая ставится следующим образом. Пусть точка $M$ равномерно движется по некоторой заданной кривой. Требуется найти траекторию равномерного движения точки $N$ такую, что касательная, проведённая к траектории в любой момент движения, проходила бы через соответствующее этому моменту положение точки $M$.

История

Задача о кривой погони поставлена Леонардо да Винчи и решена Бугером в 1732 году.

Общий случай постановки задачи

Чтобы вывести уравнение линии, выберем системы координат, в которой ось абсцисс проходит через начальное положение точек $P$ и $A$, и точка $A$ находится в начале системы координат xAy. Отношение постоянных скоростей точек обозначим через k.

Если допустить, что за бесконечно малый промежуток времени точка $P$ прошла расстояние $dS$, а точка $A$ — расстояние $dS_{1}$, то , согласно поставленному выше условию, получим соотношение $dS=kdS_{1}$, или

${\sqrt {dx^{2}+dy^{2}}}=k{\sqrt {d\xi ^{2}+d\eta ^{2}}}.$ (1)

Далее следует выразить $d\xi$ и $d\eta$ через x, y и их дифференциалы. По условию, координаты точки $P$ должны удовлетворять уравнению касательной к искомой кривой, то есть

$\eta -y={\frac {dy}{dx}}(\xi -x).$

Добавляя к этосу уравнению заданное условием уравнение траектории $F(\xi ,\eta )$ движения «убегающего», можно определить из полученной системы уравнения $\xi$ и $\eta$. После подстановки этих значений в дифференциальное уравнение (1) оно запишется в виде

$\Phi \left(x,y,{\frac {dy}{dx}},{\frac {d^{2}y}{dx^{2}}}\right)=0$.

Постоянные интегрирования могут быть найдены из начальных условий ($y=0;y'=0$ при $x=0$).

В общем случае для произвольно заданной кривой $F(\xi ,\eta )$ найти решение полученного уравнения достаточно сложно. Задача существенно упрощается, если рассмотреть простейший случай, когда траектория "убегающего" является прямой.

Практическое применение

Задача построения кривой погони впервые встала при выборе курса судна с учётом внешних факторов (боковых ветров, течения) для оптимального достижения точки цели путешествия.

Вновь эта проблема возникла при использовании в военных целях подводных лодок, торпед, а позднее и управляемых ракет с целью достижения и поражения движущихся целей. Кроме того, кривая погони применяется в космической навигации.

Вариации и обобщения

• В более широком понимании равномерности движения точки $N$ не требуется, и именно в таком понимании является кривой погони Трактриса.