Точки Аполлония

Точки Аполлония выделены зелёным

Точки Аполлония (иногда изодинамические центры) — две такие точки, расстояние от которых до вершин треугольника обратно пропорциональны сторонам, которые противолежат этим вершинам.

Свойства

• Окружности, построенные как на диаметре на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
• Точки Аполлония лежат на прямой, соединяющей центр описанной окружности с точкой Лемуана. Эта прямая называется осью Брокара.
• Подерные треугольники точек Аполлония правильные (иногда это свойство принимается за определение).
• Последнее свойство можно сформулировать иначе: три ортогональные проекции точек Аполлония на стороны данного треугольника являются вершинами правильного треугольника.
• Точки Аполлония изогонально сопряжены точкам Торричелли.
• Построим две прямые, каждая из которых проходит через точку Аполлония и точку Торричелли, отличную от изогонально сопряжённой ей. Такие прямые пересекутся в точке пересечения медиан (в центроиде треугольника).

Окружность и точка Парри. (G — центроид, а J и K являются точками Аполлония треугольника ABC)

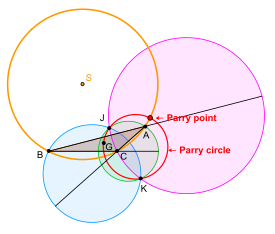
• Пусть ABC — треугольник на плоскости. Окружность, проходящая через центроид и две точки Аполлония треугольника ABC, называется окружностью Парри треугольника ABC (на рисунке справа она красная). Она также проходит через точку Парри (красная точка в черном кольце).
• Рассмотрим три сферы, касающиеся плоскости в точках $A,B,C$ и друг друга внешним образом. Если радиусы этих сфер равны $x,y,z$, то $AB={\sqrt {xy}}$ и т. д. Поэтому две сферы касающиеся трёх данных и плоскости, будут касаться плоскости в точках Аполлония.

Пример применения точки Аполлония к решению задачи Аполлония

Задача Аполлония — построить с помощью циркуля и линейки окружность, касающуюся трех данных окружностей. Один из вариантов этой задачи, когда третья окружность касается трёх внутренних внешним образом, решается с помощью введения так называемой точки Аполлония Ap (Apollonius point).

• Точка Аполлония Ap в Энциклопедии центров треугольника именуется как центр треугольника под именем X(181).
• Окружность Аполлония касается трех вневписанных окружностей вне треугольника внутренним образом (см. зеленую окружность на рисунке).

Окружность Аполлония

Определение окружности Аполлония

Точка Аполлония и окружность Аполлония

• Пусть дан треугольник ABC. Пусть вневписанные окружности треугольника ABC, противоположные вершинам A, B и C, есть соответственно E_A, E_B, E_C (см. рисунок). Тогда окружность Аполлония E (на рис. справа показана зеленым цветом) касается внутренним образом сразу трех вневписанных окружностей треугольника ABC в точках соответственно E_A, E_B и E_C (см. рисунок).

• Решением упомянутой выше частной задачи Аполлония является указанная окружность E, касающаяся трех данных окружностей E_A, E_B и E_C внешним образом.

Радиус окружности Аполлония

Радиус окружности Аполлония равен ${\frac {r^{2}+s^{2}}{4r}}$, где r — радиус вписанной окружности и s — полупериметр треугольника.

Определение точки Аполлония Ap

• Точка Аполлония Ap или X(181) определяется следующим образом:

Пусть A' , B' и C' есть точки касания окружности Аполлония E с соответствтвующими вневписанными окружностями. Тогда прямые AA' , BB' и CC' пересекаются в одной точке Ap, которую называют точкой Аполлония треугольника ABC.

Замечание

На рисунке указанная точка Аполлония Ap изображена, как точка пересечения трех перпендикуляров к сторонам треугольника ABC, опущенных из точек касаний A' , B' и C' с соответсвующими вневписанными окружностями треугольника ABC, образованного совместными попарными касательными линиями трех упомянутых выше окружностей E_A, E_B и E_C. Хотя эта точка Ap лежит в точке пересечения трех отрезков AA' , BB' и CC' , но они не перпендикулярны сторонам треугольника. Действительно, её проекции на стороны треугольника ABC являются вершинами равностороннего треугольника, а перпендикуляры к сторонам треугольника пересекаются в его ортоцентре. Проекции ортоцентра на стороны треугольника не являются вершинами равностороннего треугольника. Ортоцентр и точка Аполлония Ap совпадают только у равностороннего треугольника. У других треугольников они не совпадают.

Трилинейные координаты

Трилинейные координаты точки Аполлония Ap:

( a ( b + c )² / ( b + c − a ) : b ( c + a )² / ( c + a − b ) : c ( a + b )² / ( a + b − c )

=( ( sin A cos ( B/2 − C/2 ) )² : ( sin B cos (C/2 − A/2) )² : ( sin C cos (A/2 − B/2) )² )

См. также

• Аполлоний Пергский
• Геометрия треугольника
• Замечательные точки треугольника
• Задача Аполлония
• Изодинамические центры = Isodynamic point (англ.)
• Окружность Аполлония
• Окружность Парри
• Теорема Аполлония
• Точки Торричелли
• Точка Ферма
• Треугольник
• Отрезки и окружности, связанные с треугольником

Ссылки

• Moon, Tarik Adnan (2010), "The Apollonian circles and isodynamic points" (PDF), Mathematical Reflections (6).