Код Прюфера: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
→Свойства: пунктуация |
→Восстановление дерева: пунктуация, орфография |
||
| Строка 34: | Строка 34: | ||
== Восстановление дерева == |
== Восстановление дерева == |
||
Для |
Для восстановления дерева по коду <math>p=(p_1,\dots,p_{n-2})</math>, |
||
заготовим список номеров вершин <math>s=(1,\dots,n)</math>. |
заготовим список номеров вершин <math>s=(1,\dots,n)</math>. |
||
Выберем первый номер <math>i_1</math> который не встречается в коде. |
Выберем первый номер <math>i_1</math>, который не встречается в коде. |
||
Добавим ребро <math>(i_1, p_1)</math> после этого удалим <math>i_1</math> из <math>s</math> и <math>p_1</math> из <math>p</math>. |
Добавим ребро <math>(i_1, p_1)</math>, после этого удалим <math>i_1</math> из <math>s</math> и <math>p_1</math> из <math>p</math>. |
||
Повторяем процесс до момента |
Повторяем процесс до момента, когда код <math>p</math> становится пустым. |
||
В этот момент список <math>s</math> содержит ровно два числа <math>i_{n-1}</math> и <math>n</math>. |
В этот момент список <math>s</math> содержит ровно два числа <math>i_{n-1}</math> и <math>n</math>. |
||
Остаётся добавить ребро <math>(i_{n-1},n)</math> и дерево построено. |
Остаётся добавить ребро <math>(i_{n-1},n)</math>, и дерево построено. |
||
Версия от 06:02, 16 ноября 2017

Код Прюфера однозначно сопоставляет произвольному конечному дереву последовательность; дереву с вершинами сопоставляется последовательность из чисел от до с возможными повторениями. Код может быть получен применением простого итерационного алгоритма; также есть алгоритм, восстанавливающий дерево по его коду Прюфера.
Код Прюфера был использован Хайнцем Прюфером при доказательстве формулы Кэли в 1918 году.[1]
Построение
Пусть есть дерево с вершинами занумерованными числами . Построение кода Прюфера дерева T ведётся путем последовательного удаления вершин из дерева, пока не останутся только две вершины. При этом каждый раз выбирается концевая вершина с наименьшим номером и в код записывается номер единственной вершины, с которой она соединена. В результате получаем последовательность , составленную из чисел , возможно с повторениями.
Пример
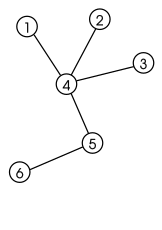
Для дерева на диаграмме вершина 1 является концевой вершиной с наименьшим номером, поэтому она удаляется и 4 ставится в код Прюфера.
Вершины 2 и 3 удаляются в следующем, так что 4 добавляется в два раза.
Вершина 4 сейчас теперь стала концевой и имеет наименьший номер, поэтому её удаляем и мы добавляем 5 к последовательности.
Мы остались только с двумя вершинами, поэтому мы останавливаемся.
В результате код Прюфера (4,4,4,5).
Восстановление дерева
Для восстановления дерева по коду , заготовим список номеров вершин . Выберем первый номер , который не встречается в коде. Добавим ребро , после этого удалим из и из .
Повторяем процесс до момента, когда код становится пустым. В этот момент список содержит ровно два числа и . Остаётся добавить ребро , и дерево построено.
Свойства
- Если — это степень вершины с номером , то встречается в коде Прюфера раз.
Приложения
- Из кода Прюфера следует Формула Кэли, то есть число остовных деревьев полного графа с вершинами равно . Доказательство следует из того, что код Прюфера даёт биекцию между остовными деревьями и последовательностями длины из чисел.
- Код Прюфера также позволяет обобщить формулу Кэли на случай, если даны степени вершин, если это последовательность степеней дерева, то число деревьев с такими степенями равно мультиноминальному коэффициенту
- Код Прюфера используется для построений случайных деревьев.
Ссылки
- ↑ Prüfer, H. (1918). "Neuer Beweis eines Satzes über Permutationen". Arch. Math. Phys. 27: 742—744.
{{cite journal}}: Указан более чем один параметр|author=and|last=(справка)