Эпициклоида

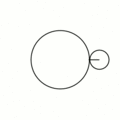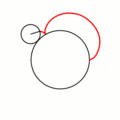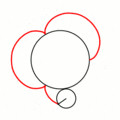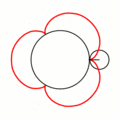
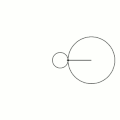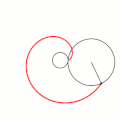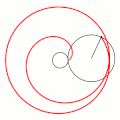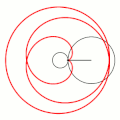
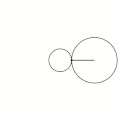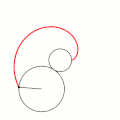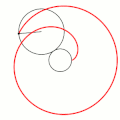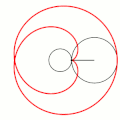
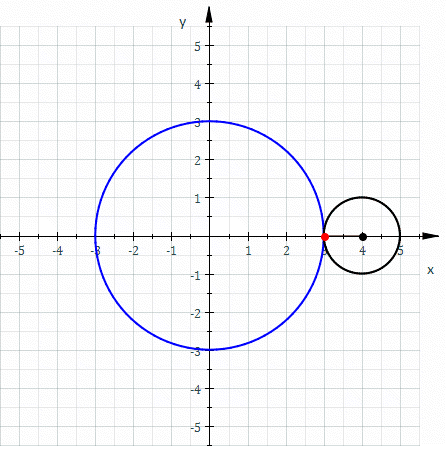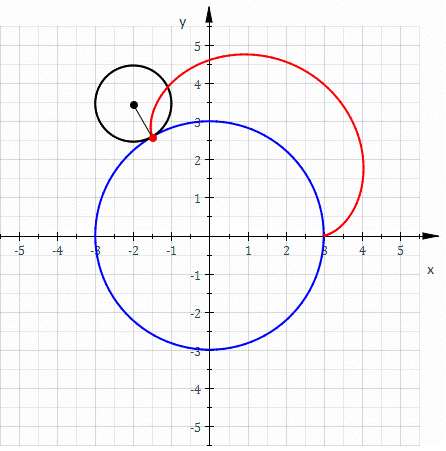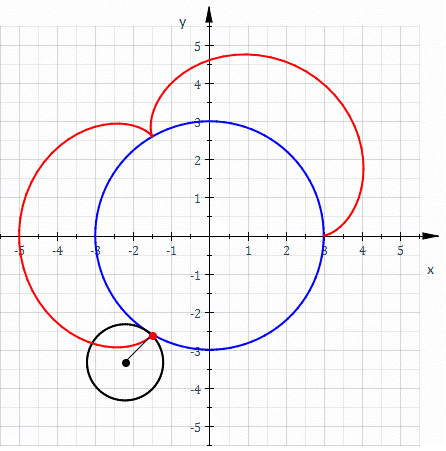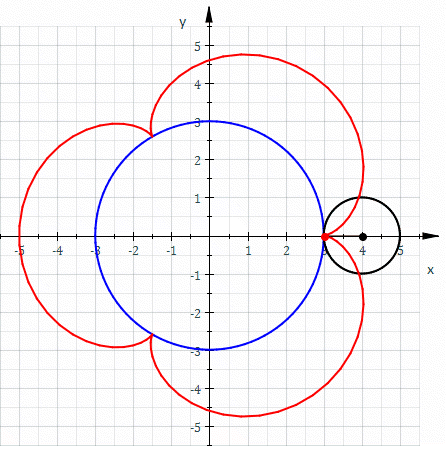
Эпицикло́ида (от др.-греч. ὲπί — на, над, при и κύκλος — круг, окружность) — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.

Уравнения

Если центр неподвижной окружности находится в начале координат, её радиус равен $R$, радиус катящейся по ней окружности равен $r$, то эпициклоида описывается параметрическими уравнениями относительно $\varphi$:

${\begin{cases}x=(R+r)\cos \varphi +r\cos(\alpha +{\frac {R+r}{r}}\varphi )\\y=(R+r)\sin \varphi +r\sin(\alpha +{\frac {R+r}{r}}\varphi )\end{cases}}$

где $\alpha$ — угол поворота точки, описывающей эпициклоиду, относительно центра подвижной окружности в момент начала движения, $\varphi$ — параметр, но фактически это угол наклона отрезка между центрами к оси $OX$.

Можно ввести величину $\textstyle k={\frac {R}{r}}$, тогда уравнения предстанут в виде

${\begin{cases}x=r(k+1)\left(\cos \varphi -{\frac {\cos((k+1)\varphi )}{k+1}}\right)\\y=r(k+1)\left(\sin \varphi -{\frac {\sin((k+1)\varphi )}{k+1}}\right)\end{cases}}$

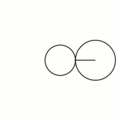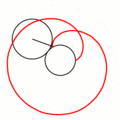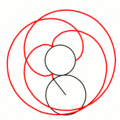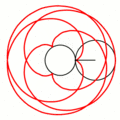
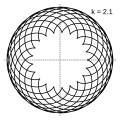
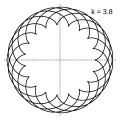
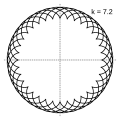
Величина $k$ определяет форму эпициклоиды. При $k=1$ эпициклоида образует кардиоиду, а при $k=2$ — нефроиду. Если $k$ — несократимая дробь вида ${\frac {m}{n}}$ ($m,n\in \mathbb {N}$), то $m$ — это количество каспов данной эпициклоиды, а $n$ — количество полных вращений катящейся окружности. Если $k$ иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.

• Эпициклоиды при разных значениях параметра k:
• 
  $k=1$ (кардиоида)
• 
  $k=2$ (нефроида)
• 
  $k=3$
• 
  $k={\frac {3}{4}}$
• 
  $k={\frac {1}{3}}$
• 
  $k=0.5={\frac {1}{2}}$
• 
  $k=2.1={\frac {21}{10}}$
• 
  $k=3.8={\frac {19}{5}}$
• 
  $k=5.5={\frac {11}{2}}$
• 
  $k=7.2={\frac {36}{5}}$

См. также

• Циклоида
• Гипоциклоида
• Эпитрохоида