Теорема Кёнига (комбинаторика)

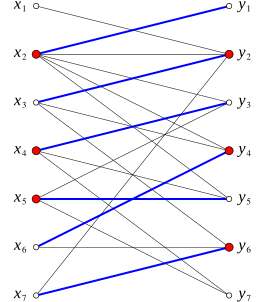
Пример двудольного графа с наибольшим паросочетанием (выделено голубым) и наименьшим вершинным покрытием (выделено красным), оба имеют размер шесть.

В теории графов теорема Кёнига, доказанная Денешем Кёнигом в 1931, утверждает эквивалентность задач нахождения наибольшего паросочетания и наименьшего вершинного покрытия в двудольных графах. Это же было независимо открыто, в том же 1931, венгерским математиком Йенё Эгервари^[англ.] в несколько более общем виде для случая взвешенных графов.

Кёниг опубликовал в 1916 доказательство, что любой регулярный двудольный граф имеет совершенное паросочетание,^[1] и, обобщённо, что хроматический индекс любого двудольного графа (то есть наименьшее число паросочетаний, на которые можно разложить все рёбра графа) равен максимальной степени его вершин^[2]. Последнее утверждение известно как теорема Кёнига о рёберной раскраске.^[3] Бонди и Мёрти (Bondy, Murty, 1976) приписывают саму теорему более поздней работе Кёнига (1931). Согласно Бигу (Bigg), Кёниг приписывает идею изучения паросочетаний в двудольных графах своему отцу, математику Юлиусу Кёнигу^[англ.].

Определения

Граф называется двудольным, если его вершины можно разбить на два множества так, что у каждого ребра конечные вершины принадлежат разным множествам.

Вершинное покрытие графа — это множество вершин, такое, что любое ребро графа имеет хотя бы одну конечную вершину из этого множества. Вершинное покрытие называется наименьшим, если никакое другое вершинное покрытие не имеет меньшего числа вершин.

Паросочетанием в графе называется множество рёбер, не имеющих общих конечных вершин. Паросочетание называется наибольшим, если никакое другое паросочетание не содержит большего числа рёбер.

Утверждение теоремы

В любом двудольном графе число рёбер в наибольшем паросочетании равно числу вершин в наименьшем вершинном покрытии.

Пример

Двудольный граф на рисунке вверху имеет по 7 в каждой из долей. Паросочетание с 6 рёбрами выделено синим цветом, а вершинное покрытие $\{x_{2},x_{4},x_{5},y_{2},y_{4},y_{6}\}$ выделено красным. Это покрытие является наименьшим по размеру, поскольку любая вершина в покрытии должна включать по меньшей мере одну конечную вершину ребра паросочетания. Таким же образом, нет паросочетания большего размера, поскольку любое ребро паросочетания должно содержать по меньшей мере одну конечную вершину из вершинного покрытия, так что это паросочетание является наибольшим. Теорема Кёнига как раз и утверждает равенство размеров паросочетания и покрытия (в данном примере оба числа равны шести).

Доказательство ^{[источник не указан 1659 дней]}

Разделение вершин на посещённые и не посещённые для доказательства теоремы Кёнига.

Пусть задан двудольный граф $G=(X,Y,E)$ , а $M$ — наибольшее паросочетание в $G$ .

Сначала рассмотрим случай, когда паросочетание $M$ насыщает все вершины доли $X$ , то есть размер паросочетания $M$ равен $|X|$ . Очевидно, что вся доля $X$ является вершинным покрытием в графе $G$ , следовательно, она является и наименьшим вершинным покрытием, и в этом случае утверждение теоремы выполняется.

Иначе возьмём все вершины доли $X$ , не насыщенные паросочетанием $M$ , и запустим из них обход в ширину по следующему правилу:

Слева направо переходим только по рёбрам, не входящим в $M$ (будем называть их чёрными).
Справа налево переходим только по рёбрам, входящим в $M$ (будем называть их голубыми).

Пусть $X^{+}$ и $Y^{+}$ — подмножества вершин левой и правой доли, посещённых во время обхода, а $X^{-}$ и $Y^{-}$ — соответственно, подмножества не посещённых вершин (см. рисунок справа).

Между множествами $X^{+}$ и $Y^{-}$ нет чёрных рёбер, поскольку иначе во время обхода мы бы посетили вершины из множества $Y^{-}$ . По аналогичной причине, между множествами $X^{-}$ и $Y^{+}$ нет голубых рёбер.

Докажем, что между множествами $X^{+}$ и $Y^{-}$ нет также и голубых рёбер. От противного, пусть такое ребро $\{x^{+},y^{-}\}$ есть. Вершина $x^{+}$ не могла являться стартовой для обхода в ширину, поскольку она насыщена паросочетанием $M$ . Следовательно, обход в ширину пришёл в $x^{+}$ из какой-то вершины $y^{+}$ по голубому ребру, что означает, что вершине $x^{+}$ инцидентны два голубых ребра $\{x^{+},y^{-}\}$ и $\{x^{+},y^{+}\}$ . Но это невозможно, поскольку голубые рёбра образуют паросочетание.

Следовательно, любое ребро графа G инцидентно или вершине из $X^{-}$ или вершине из $Y^{+}$ , то есть $X^{-}\cup Y^{+}$ является вершинным покрытием. Покажем, что все вершины в $X^{-}\cup Y^{+}$ насыщены паросочетанием $M$ . Для вершин из $X^{-}$ это очевидно, поскольку все ненасыщенные вершины левой доли по построению лежат в $X^{+}$ . Если в $Y^{+}$ есть ненасыщенная вершина, то существует $M$ -чередующая цепь, заканчивающаяся в ней, что противоречит тому, что паросочетание $M$ является наибольшим. Теперь осталось вспомнить, что между множествами $X^{-}$ и $Y^{+}$ нет рёбер из $M$ , то есть каждому ребру паросочетания инцидентна в точности одна вершина из вершинного покрытия $X^{-}\cup Y^{+}$ . Следовательно, $|M|=|X^{-}\cup Y^{+}|$ , и вершинное покрытие $X^{-}\cup Y^{+}$ является наименьшим.

Следствие из теоремы Кёнига

Пусть $M$ и $C$ — соответственно, наибольшее паросочетание и наименьшее вершинное покрытие в двудольном графе $G$ . Тогда любое ребро из $M$ инцидентно в точности одной вершине из $C$ . И наоборот, любой вершине из $C$ инцидентно в точности одно ребро из $M$ . Другими словами, отношение инцидентности задаёт биекцию между множествами $M$ и $C$ .

Заметим, что если бы граф $G$ не являлся двудольным, то некоторым рёбрам $M$ могли бы быть инцидентны сразу две вершины из $C$ , а некоторые вершины из $C$ могли бы не иметь инцидентных им рёбер из $M$ .

Алгоритмы построения наименьшего вершинного покрытия в двудольном графе ^{[источник не указан 1659 дней]}

Алгоритм 1

Описанный выше обход в ширину из доказательства теоремы строит наименьшее вершинное покрытие по заданному наибольшему паросочетанию.

Реализация алгоритма на C++:

Предполагаем, что граф содержит x_count вершин в левой доле, y_count вершин в правой доле, а его рёбра заданы списками смежности x_lists (x_lists[x] содержит список вершин правой доли, смежных с вершиной x). Паросочетание $M$ задано массивами x_matching и y_matching, хранящими левого и правого соседа каждой вершины; если вершина не насыщена $M$ , то в соответствующей ячейке записано число -1. Массивы x_label и y_label обозначают, были ли посещены соответствующие вершины во время обхода в ширину. Наконец, в массивы x_cover и y_cover записывается найденное покрытие: x_cover[x_cover[x] == true] x_cover[x] == true (или, соответственно, y_cover[y] == true), если вершина x (y) входит в наименьшее вершинное покрытие.

  for (int x = 0; x < x_count; x++)
     x_label[x] = false;

  for (int y = 0; y < y_count; y++)
     y_label[y] = false;

  queue<int> x_queue;
  for (int x = 0; x < x_count; x++)
     if (x_matching[x] == -1)
     {
        x_queue.push(x);
        x_label[x] = true;
     }

  while (!x_queue.empty())
  {
     const int x = x_queue.front();
     x_queue.pop();

     for (int y : x_lists[x])
        if (!y_label[y])
        {
           y_label[y] = true;
           int new_x = y_matching[y];
           x_label[new_x] = true;
           x_queue.push(new_x);
        }
  }

  for (int x = 0; x < x_count; x++)
     x_cover[x] = !x_label[x];

  for (int y = 0; y < y_count; y++)
     y_cover[y] = y_label[y];

Данный алгоритм имеет сложность $O(|E|)$ . Поскольку алгоритм Хопкрофта–Карпа находит наибольшее паросочетание в двудольном графе за время $O(|E|{\sqrt {|V|}})$ , за это же время в заданном графе может быть найдено и наименьшее вершинное покрытие.

Алгоритм 2

Есть более простой итеративный алгоритм построения наименьшего вершинного покрытия по наибольшему паросочетанию $M$ . Этот алгоритм модифицирует множества вершин $X'\subseteq X$ , $Y'\subseteq Y$ , до тех пор пока $X'\cup Y'$ не станет вершинным покрытием.

Положим $X'=X_{M}$ , $Y'=\emptyset$ , где $X_{M}$ — это множество вершин доли $X$ , насыщенных паросочетанием $M$ .
Пока в графе есть хотя бы одно ребро $\{x,y\}$ $\{x,y\}$ , не покрытое множеством вершин $X'\cup Y'$ $X'\cup Y'$ (т.е. $x\notin X'$ $x\notin X'$ и $y\notin Y'$ $y\notin Y'$ ):
1. Найдём вершину $x^{*}\in X'$ такую, что $\{x^{*},y\}\in M$ (почему такая вершина всегда существует, см. далее).
2. Положим $X'=X'-x^{*}$ ; $Y'=Y'+y$ .

Доказательство корректности и оценка количества итераций:

Нужно показать, что на каждой итерации алгоритма найдётся нужная вершина $x^{*}$ . Для этого мы докажем, что во время работы алгоритма сохраняются следующие инварианты:

$X'\cup Y'$ покрывает все рёбра паросочетания $M$ , причём $|X'\cup Y'|=|M|$ .
Если $C$ — некоторое минимальное вершинное покрытие, а $X_{C}$ и $Y_{C}$ — его, соответственно, левая и правая доли, то $X_{C}\subseteq X'$ , а $Y\subseteq Y_{C}$ .

В начале работы алгоритма оба инварианта очевидно выполняются. Далее, рассуждая по индукции, рассмотрим, что происходит во время каждой итерации алгоритма, предполагая, что к её началу оба инварианта выполнялись.

Из того, что $C$ — вершинное покрытие, следует, что $C$ покрывает и ребро $\{x,y\}$ , то есть $x\in X_{C}$ или $y\in Y_{C}$ . Первое невозможно, т.к. по предположению индукции $X_{C}\subseteq X'$ (второй инвариант), а $x\notin X'$ . Следовательно, $y\in Y_{C}$ . Значит, $y$ , как вершина из минимального вершинного покрытия, инцидентна некоторому ребру наибольшего паросочетания $M$ (см. следствие из теоремы Кёнига) — обозначим это ребро $\{x^{*},y\}$ . По предположению индукции, множество $X'\cup Y'$ покрывает ребро $\{x^{*},y\}$ (первый инвариант). Но $y\notin Y'$ , следовательно, $x^{*}\in X'$ .

Далее заметим, что модификация множеств $X'$ и $Y'$ заключается в том, что мы заменяем левую вершину одного из рёбер паросочетания $M$ на правую, поэтому первый инвариант сохраняется.

Далее, из $y\in Y_{C}$ следует $x^{*}\notin X_{C}$ , поскольку ребро паросочетания $M$ не может быть инцидентно сразу двум вершинам из наименьшего вершинного покрытия. Значит, убрав из $X'$ вершину $x^{*}$ и добавив в $Y'$ вершину $y$ , мы не нарушим инвариант $X_{C}\subseteq X'$ , $Y\subseteq Y_{C}$ .

Когда алгоритм завершит свою работу, очевидно, что $X'\cup Y'$ будет вершинным покрытием графа. Поскольку $|X'\cup Y'|=|M|$ (первый инвариант), это вершинное покрытие будет являться наименьшим.

Теперь оценим количество итераций работы алгоритма. На каждой итерации размер множества $X'\setminus X_{C}$ уменьшается на единицу, а когда $X'$ совпадёт с $X_{C}$ , алгоритм завершит работу. Следовательно, всего будет выполнено не более $|M|-|X_{C}|$ итераций. Алгоритм может завершить работу и раньше, если в графе есть вершинное покрытие с размером левой доли более $|X_{C}|$ . На самом деле, мы доказали, что алгоритм найдёт минимальное вершинное покрытие с максимально возможным размером левой доли (поскольку, доказывая, что $X_{C}\subseteq X'$ , никак не ограничивали выбор вершинного покрытия $C$ ).

Реализация алгоритма на C++:

Здесь используются те же обозначения, что и в реализации первого алгоритма.

  for (int x = 0; x < x_count; x++)
     x_cover[x] = x_matching[x] != -1;

  for (int y = 0; y < y_count; y++)
     y_cover[y] = false;

  bool ind = true;
  while (ind)
  {
     ind = false;
     for (int x = 0; x < x_count; x++)
        for (int y : x_lists[x])
           if (!x_cover[x] && !y_cover[y])
           {
              x_cover[y_matching[y]] = false;
              y_cover[y] = true;
              ind = true;
           }
  }

Данная реализация имеет сложность $O(|M||E|)$ .

Связь с совершенными графами

Говорят, что граф совершенен, если для любого порождённого подграфа его хроматическое число равно размеру максимальной клики. Любой двудольный граф совершенен, поскольку любой его подграф является либо двудольным, либо независимым. В двудольном графе, не являющемся независимым, хроматическое число и размер максимальной клики равны двум, в то время как для независимого множества оба этих числа равны единице.

Граф совершенен тогда и только тогда, когда его дополнение совершенно (Lovász 1972), и теорему Кёнига можно считать эквивалентом утверждения, что дополнение двудольного графа совершенно. Любые раскраски дополнения двудольного графа имеют размер максимум 2, а классы размера 2 образуют паросочетания. Клики в дополнении графа G — это независимое множество в G, и, как мы уже писали выше, независимое множество в двудольном графе G — это дополнение вершинного покрытия G. Таким образом, любое паросочетание M в двудольном графе G с n вершинами соответствует раскраске дополнения G с n-|M| цветами, что, ввиду совершенства дополнения двудольных графов, соответствует независимому множеству в G с n-|M| вершинами, что соответствует вершинному покрытию G |M| вершинами. Следовательно, теорема Кёнига доказывает совершенство дополнений двудольных графов, то есть результат, выраженный в более явной форме у Галаи (Gallai, 1958).

Можно связать также теорему Кёнига о рёберной раскраске с другим классом совершенных графов, рёберными графами двудольных графов. Для графа G рёберный граф L(G) имеет вершины, соответствующие рёбрам графа G, и рёбра для каждой пары смежных рёбер в G. Таким образом, хроматическое число L(G) равно хроматическому индексу G. Если G — двудольный, клики в L(G) — это в точности множества рёбер в G, имеющих общую конечную вершину. Теперь теорема Кёнига о рёберной раскраске, утверждающая, что хроматический индекс равен максимальной степени вершин в двудольном графе, может быть интерпретирована как утверждение, что рёберный граф двудольного графа совершенен.

Поскольку рёберные графы двудольных графов совершенны, дополнения рёберных графов двудольных графов тоже совершенны. Клика в дополнении рёберного графа для G — это просто паросочетание G. А раскраска дополнения рёберного графа для G, в случае, если G является двудольным, — это разбиение рёбер графа G на подмножества рёбер, имеющих общие вершины. Конечные вершины, являющиеся общими в этих подмножествах, образуют вершинное покрытие графа G. Таким образом, сама теорема Кёнига может быть также интерпретирована как утверждение, что дополнение рёберных графов двудольных графов совершенно.

Дополнения

Для графов, не являющихся двудольными, ситуация с задачами о наибольшем паросочетании и наименьшем вершинном покрытии совсем другая — наибольшее паросочетание можно найти за полиномиальное время для любого графа, в то время как поиск наименьшего вершинного покрытия является NP-полной задачей. Дополнение вершинного покрытия для любого графа — это независимое множество, и поиск наибольшего независимого множества — это ещё одна NP-полная задача.
Теорема Кёнига эквивалентна массе других минимаксных теорем в теории графов и комбинаторике, таких как теорема Холла о свадьбах и теорема Дилуорса. Поскольку паросочетание в двудольных графах является частным случаем потока в сети, теорема Кёнига также вытекает из теоремы Форда — Фалкерсона.
В русскоязычном интернете и научной литературе распространена следующая формулировка теоремы^[4]: если прямоугольная матрица составлена из нулей и единиц, то минимальное число линий, содержащих все единицы, равно максимальному числу единиц, которые могут быть выбраны так, чтобы никакие две из них не лежали на одной и той же линии (термин «линия» обозначает либо строку, либо столбец в матрице).^[5]

Вопреки эквивалентности двух задач с точки зрения точного решения, они совершенно не эквивалентны для аппроксимационных алгоритмов. Задача о наибольшем паросочетании для двудольных графов может быть аппроксимирована с произвольной точностью за постоянное время с помощью распределённых алгоритмов^[англ.], в противоположность задаче о наименьшем вершинном покрытии, требующей как минимум логарифмического времени.^[6]

Замечания

↑ На плакате, выставленном в 1998 на Международном конгрессе математиков в Берлине, а затем на Международной конференции по теории графов Bled'07, Геральд Гроп (Harald Gropp) указал на то, что тот же самый результат уже появлялся на языке конфигураций в 1894 в тезисах Эрнста Штайница.
↑ Biggs, 1976.
↑ Lovász, 1986, Theorem 1.4.17, с. 37.
↑ Рыбников, 1972, с. 100.
↑ Вопросы кибернетики. Тр. Семинара по комбинаторной математике. — М., 1973. — С. 185—99..
↑ Göös, 2012.

Ссылки

А. Ю. Эвнин. Вокруг теоремы Холла (рус.) // Матем. обр.. — 2005. — Т. 3(34). — С. 2—23.

Biggs, N. L.; Lloyd, E. K.; Wilson, R. J. Graph Theory 1736–1936. — Oxford University Press, 1976. — С. 203–207. — ISBN 0-19-853916-9.

J. A. Bondy, U. S. R. Murty. Graph Theory with Applications. — North Holland, 1976. — С. 74. — ISBN 0-444-19451-7.

Gallai, Tibor. Maximum-minimum Sätze über Graphen // Acta Math. Acad. Sci. Hungar.. — 1958. — Т. 9, вып. 3-4. — С. 395–434. — doi:10.1007/BF02020271.

Mika Göös, Jukka Suomela. 26th International Symposium on Distributed Computing (DISC), Salvador, Brazil, October 2012. — 2012.

Kőnig, Dénes. Gráfok és alkalmazásuk a determinánsok és a halmazok elméletére // Matematikai és Természettudományi Értesítő. — 1916. — Т. 34. — С. 104–119.

Kőnig, Dénes. Gráfok és mátrixok // Matematikai és Fizikai Lapok. — 1931. — Т. 38. — С. 116–119.

László Lovász, M. D. Plummer. Matching Theory. — North-Holland, 1986. — ISBN 0-444-87916-1.

Lovász, László. Normal hypergraphs and the perfect graph conjecture // Discrete Mathematics. — 1972. — Т. 2, вып. 3. — С. 253–267. — doi:10.1016/0012-365X(72)90006-4.

Литература

Рыбников К.А. Введение в комбинаторный анализ. — МГУ, 1972.

[1] На плакате, выставленном в 1998 на Международном конгрессе математиков в Берлине, а затем на Международной конференции по теории графов Bled'07, Геральд Гроп (Harald Gropp) указал на то, что тот же самый результат уже появлялся на языке конфигураций в 1894 в тезисах Эрнста Штайница.

[_da370c94fd5cacb2-2] Biggs, 1976.

[_619110571a748430-3] Lovász, 1986, Theorem 1.4.17, с. 37.

[_2dab55a19b9f8cc3-4] Рыбников, 1972, с. 100.

[5] Вопросы кибернетики. Тр. Семинара по комбинаторной математике. — М., 1973. — С. 185—99..

[_877e41dc29d1d908-6] Göös, 2012.

[1]

[2]

[3]

[4]

[5]

[6]

Теорема Кёнига (комбинаторика)

Содержание

Определения

Утверждение теоремы

Пример

Доказательство ^{[источник не указан 1659 дней]}

Следствие из теоремы Кёнига

Алгоритмы построения наименьшего вершинного покрытия в двудольном графе ^{[источник не указан 1659 дней]}

Алгоритм 1

Реализация алгоритма на C++:

Алгоритм 2

Доказательство корректности и оценка количества итераций:

Реализация алгоритма на C++:

Связь с совершенными графами

Дополнения

Замечания

Ссылки

Литература

Навигация

Теорема Кёнига (комбинаторика)

Определения

Утверждение теоремы

Пример

Следствие из теоремы Кёнига

Алгоритмы построения наименьшего вершинного покрытия в двудольном графе [источник не указан 1659 дней]

Алгоритм 1

Реализация алгоритма на C++:

Алгоритм 2

Доказательство корректности и оценка количества итераций:

Реализация алгоритма на C++:

Связь с совершенными графами

Дополнения

Замечания

Ссылки

Литература

Навигация

Поиск

Алгоритмы построения наименьшего вершинного покрытия в двудольном графе ^{[источник не указан 1659 дней]}