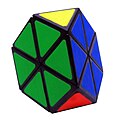
Пирамидка Мефферта
| Пирамидка Мефферта Молдавская пирамидка Японский тетраэдр Тетраэдр Рубика | |
|---|---|
| Pyraminx | |
 | |
| Основная информация | |
| Изобретатель | Уве Мефферт |
| Год выпуска | 1972 |
| Кол-во возможных комбинаций | 75 582 720 |
| Число Бога | 11 ходов |
| Форма | тетраэдр |
Пирамидка Мефферта (англ. Pyraminx), «Молдавская пирамидка» или «Японский тетраэдр» — головоломка в форме правильного тетраэдра, подобная кубику Рубика. Каждая грань тетраэдра поделена на 9 правильных треугольников. Задача состоит в том, чтобы перевести пирамидку в конфигурацию с одноцветными гранями.
Иногда за схожесть с кубическим аналогом называют также «Тетраэдр Рубика», хотя Эрнё Рубик не имеет никакого отношения к созданию этой головоломки.
История
Головоломка была изобретена и запатентована в 1972 году (до изобретения кубика Рубика) немцем Уве Меффертом, однако популярность игрушка приобрела после выхода кубического аналога и с 1981 года выпускается японской корпорацией «Tomy Toys» (на тот момент — третья в мире по величине компания по выпуску игрушек). В СССР тетраэдр изобрёл в 1981 году инженер, главный технолог Кишинёвского тракторного завода Александр Александрович Ордынец, за что головоломку также называют Молдавской пирамидкой.
Конструкция


Головоломка состоит из 14 подвижных элементов: 4 осевых (каждый из которых имеет треугольники, обращенные на 3 смежные грани), 6 рёберных и 4 тривиальных угловых. Осевые элементы имеют форму октаэдров, а рёберные и угловые — тетраэдров. При вращении частей пирамидки относительно рассекающих её плоскостей фрагменты перемещаются. Вращение происходит вокруг осей, направленных из центра к вершинам головоломки.
Конструктивно головоломка представляет собой 4-лучевую объёмную крестовину, на осях которой размещаются осевые и тривиальные элементы, а в специальным образом сформированные пазы помещены рёберные элементы, снабжённые выступами, позволяющими фрагментам свободно перемещаться при вращении головоломки, при этом не вываливаясь из неё.
Сборка
Сборка пирамидки проще сборки кубика Рубика. Взаимное расположение цветных граней осевых и тривиальных элементов задано конструкцией, и они легко выставляются в правильные положения (трилистник, аналог «креста» у кубика Рубика, только конструктивно он формируется одновременно для всех граней), после чего остаётся упорядочить 6 рёберных элементов.
Модификации
-
Мастер-пирамидка 4×4×4
-
Вариант, пирамидка Хелперн-Мейера
-
Пирамидка с элементами разной формы
-
Джинг-пирамидка
-
Тетраминкс


Существует головоломка под названием «Тетраминкс» (англ. Tetraminx) в форме усечённого тетраэдра, которая отличается от пирамидки Мефферта отсутствием тривиальных вершин.
Визуально похожая пирамидка меньшего размера — 2×2×2. Несмотря на внешнюю схожесть, она имеет принципиально другой механизм (аналогичный кубу 2×2×2). По этой причине в результате вращений форма головоломки меняется, задача сборки состоит не только в упорядочении цветов, но и в восстановлении тетраэдра[1].
Существует и просто пирамидка 2×2×2, где вращаются только тривиальные вершины.
В 2013 году Тони Фишер сделал гигантскую пирамидку и гигантский тетраминкс. В 2017 году он сделал гигантский мастер пираминкс.
По меньшей мере четыре раза разными инженерами (в том числе в СССР[2]) предпринимались попытки создать Master Pyraminx, пирамидку с 4 слоями[3][4][5][6], и с 2011 года началось их массовое производство. В 2017 году китайская фирма Shengshou(сейчас: Sengso) выпустила в массовое производство мастер мираминкс с нескруглёнными гранями.
Позднее Тимур Эвбатыров (Башкирия) изобрёл Professor Pyraminx с 5 слоями[7][8], но в настоящее время везде распродан и более не выпускается.
Calvin puzzles в 2018 году начал выпускать Royal pyraminx, он же Королевская пирамидка, аналог с 6 слоями.
Существует и семислойная версия (Emperor pyraminx), но она существует лишь как прототип в единичном экземпляре, сделанном на 3d принтере Shapeways.
Jings pyraminx - добавляем в пирамидку невидимые центры.
Скьюб - кубическая трансформация Jings pyraminx.
Если обычную пирамидку при помощи материалов превратить в куб, то выйдет кубоминкс( сделал Тони Фишер), причем он возможен как с прямыми, так и криволинейными( англ:curvy) разрезами.Последний называют "кубик плюща"( англ:Ivy cube).
У Jings pyraminx, скьюба и кубоминкса есть 4×4×4, 5×5×5 и более аналоги.
Как и крейзи кубы, есть серия пирамидок с фиксированными и подвижными кругами.
Шестеренчатая пирамидка или Gear pyraminx. По аналогии с шестеренчатым кубиком Рубика с пирамидкой проделали то же самое. Тимур Эвбатыров проделал то же самое с мастер пираминксом.
Вулкан - пазл с интересной геометрией. Его можно назвать cross pyraminx( то есть на каждую грань налеплена полностью функциональная грань) и тетраэдрической трансформацией F-скьюба( 4×4×4 скьюба) одновременно. Мини версия - Junior volcano или диноморфикс.
По аналогии с кубоидами, делали аналоги на пирамидку. Получались в форме пентаэдров.
Крейзи пентаэдры.
Пиракоптер - аналог кубик «Вертолёт», но тетраэдрический. Геометрия интересна тем, что это тот же кубик Рубика 3×3×3, и он не блокируется в отличие от вертолёта кубического. С виду выглядит точь-в-точь, как пирамидка, но вращается не за счёт вершин, а за счёт рёбер.
Ghost версия пирамидки и Jings pyraminx.
Зеркальная версия пирамидки.
Октаминкс - усекаем четыре вершины и получаем октаэдр.
Сиамские пирамидки. Или сиаминкс.
Комбинаторика
Каждый из 4 осевых и 4 вершинных элементов может быть ориентирован тремя способами независимо от состояния других элементов. Шесть рёберных элементов могут быть ориентированы 25 способами и расположены 6!/2 способами. Таким образом, число конфигураций равно
В головоломке «Тетраминкс» тривиальные вершины отсутствуют, поэтому число конфигураций меньше в 81 раз и равно 933120[9].
Оптимальное решение
Известно, что число Бога головоломки (минимально необходимое число поворотов для сборки пирамидки при оптимальном методе сборки) равно 11. Имеется всего 933 120 возможных перестановок цветов на гранях (исключая расположение тривиальных угловых элементов), что позволяет определить оптимальное решение для каждой конфигурации методом полного перебора[9][10].
Следующая таблица показывает число конфигураций, которые могут быть решены в n ходов, но не могут быть решены меньше, чем в n ходов.
| n | число конфигураций |
|---|---|
| 0 | 1 |
| 1 | 8 |
| 2 | 48 |
| 3 | 288 |
| 4 | 1728 |
| 5 | 9896 |
| 6 | 51 808 |
| 7 | 220 111 |
| 8 | 480 467 |
| 9 | 166 276 |
| 10 | 2457 |
| 11 | 32 |
См. также
Примечания
- ↑ Пирамидка 2×2
- ↑ Советские головоломки от конструктора Ордынца или кто первый изобрёл Пирамидку?
- ↑ Le Master Pyraminx / Univers Cubique / Créations — Les Forums du Refuge d’Aerie’s Guard. Дата обращения: 10 апреля 2011. Архивировано из оригинала 29 мая 2014 года.
- ↑ Master Pyraminx by shim on Shapeways (недоступная ссылка)
- ↑ TwistyPuzzles.com Forum • View topic — The Master Pyraminx — now with video
- ↑ YouTube — Master Pyraminx
- ↑ TwistyPuzzles.com Forum • View topic — Professor Pyraminx Shipping
- ↑ YouTube — Professor Pyraminx
- ↑ 1 2 Jaap Scherphuis. Pyraminx (англ.). Jaap's Puzzle Page. Дата обращения: 29 июля 2013. Архивировано 29 августа 2013 года.
- ↑ последовательность A079744 в OEIS
Литература
- И. Константинов. Вокруг кубика // Наука и Жизнь. — 1982. — № 7. — С. 100 — 102.
- В. Н. Николаев. Венгерский кубик и молдавская пирамидка (по страницам книг и журналов). Дата обращения: 29 июля 2013.
Ссылки
- Jaap Scherphuis. Pyraminx (англ.). Jaap's Puzzle Page. Дата обращения: 29 июля 2013. Архивировано 29 августа 2013 года.
- Уве Мефферт, создатель головоломки