Круговое вероятное отклонение

Рис. 1. Геометрическое представление КВО

Кругово́е вероя́тное отклоне́ние (КВО) — показатель точности попадания бомбы, ракеты, снаряда, применяемый для оценки вероятности поражения цели. Круговое рассеивание является частным случаем более общего понятия вероятного или срединного отклонения, широко используемого в артиллерийской практике и баллистике с XIX века. Как характеристика эффективности ракетного оружия КВО или по англ.  CEP (от Circular Error Probable) введено в оборот в специальной технической литературе в конце 1940-х — начале 1950-х годов.

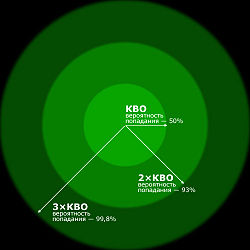
КВО выражается величиной радиуса круга, очерченного вокруг цели, в который предположительно должно попасть 50 % боеприпасов (или их боевых частей); далее для простоты они будут называться снарядами.

Рис. 2. Круговое двумерное нормальное распределение

По определению, если КВО равно L, то 50 % снарядов падает на расстояниях от цели меньших либо равных L. Если при этом места падения снарядов подчиняются некоррелированному двумерному нормальному распределению с равными стандартными отклонениями σ_x = σ_y = σ по обеим осям (часто встречающийся в практике случай, см. рис. 2), то примерно 43,7 % снарядов падают на расстояниях между L и 2L от цели, около 6,1 % — на расстояниях между 2L и 3L, и лишь 0,2 % снарядов падает на расстояниях от цели, больших, чем три величины КВО. Стандартное отклонение по любой горизонтальной оси σ связано с КВО соотношением L = σ·√2 ln 2 ≈ 1,1774 σ. Для кругового нормального распределения расстояние от точки падения снаряда до цели (промах, s) подчиняется распределению Рэлея. При этом максимум плотности кругового распределения вероятностей находится в точке цели, однако среднеквадратичный промах равен s_rms = σ·√2 ≈ 1,2011L (внутрь круга с таким радиусом попадает 63,213% снарядов, а в круг с удвоенным радиусом 2s_rms ≈ 2,4022L — 98,169% снарядов). Применительно к круговому нормальному распределению часто встречается также величина R₉₅ ≈ 2,4477 σ ≈ 2,0789 L — радиус круга с центром в цели, в который попадает 95% снарядов.

На практике распределение попаданий относительно точки прицеливания может не подчиняться круговому нормальному закону. В частности, применительно к высокоточному оружию отмечается группирование точек падения ближе к условному центру рассеивания, и, таким образом, имеет место отклонение от нормального распределения. Для артиллерийских боеприпасов при стрельбе по целям на горизонтальной поверхности характерны увеличенные значения вероятного отклонения по дальности по сравнению с вероятным отклонением в боковом направлении, с образованием доверительной области в форме эллипса (эллипс рассеивания), вытянутого по дальности. В этом случае соотношения, указанные выше, недействительны, однако концепция КВО всё ещё может использоваться, оставаясь мерой точности стрельбы (меньшее значение КВО соответствует лучшей точности стрельбы).

С увеличением дальности достижение малого КВО становится всё более трудной задачей.

Точность главным образом зависит от степени совершенства систем наведения (для управляемых боеприпасов — также и систем управления), а также от аэродинамических показателей.

Современные крылатые ракеты и управляемые (корректируемые) авиабомбы имеют КВО, не превышающее 10 метров. Самые точные баллистические ракеты имеют КВО менее 100 метров, даже при межконтинентальных дальностях. У первой баллистической ракеты «Фау-2» (V2), созданной в 1942 году и имевшей практическую дальность полёта около 250—270 километров (максимально — 320 км), КВО составляло от 4,5 до 6 км.

Сравнение по КВО

• UGM-133A Трайдент II (D5) — 90 м. с GPS
• Р-30 Булава-30 — 350 м.

Литература

• Вероятное отклонение // Вавилон — «Гражданская война в Северной Америке» / [под общ. ред. Н. В. Огаркова]. — М. : Военное изд-во М-ва обороны СССР, 1979. — (Советская военная энциклопедия : в 8 т. ; 1976—1980, т. 2).
• Задача особой государственной важности. Из истории создания ракетно-ядерного оружия и Ракетных войск стратегического назначения (1945-1959 гг.) / Сост. В. И. Ивкин, Г. А. Сухина. — М.: Российская политическая энциклопедия (РОССПЭН), 2010. — 1207 с. — 800 экз. — ISBN 978-5-8243-1430.