У этого термина существуют и другие значения, см.
Производная .
Иллюстрация понятия производной Произво́дная функции — понятие дифференциального исчисления , характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю , если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием .
Обратный процесс — нахождение первообразной — интегрирование .
В классическом дифференциальном исчислении производная чаще всего определяется через понятие предела , однако исторически теория пределов появилась позже дифференциального исчисления. Ньютон называл производную флюксией , школа Лейбница предпочитала в качестве базового понятия дифференциал [ 1]
Русский термин в форме «производная функция» впервые употребил В. И. Висковатов , переведя на русский язык соответствующий французский термин dérivée , используемый Лагранжем [ 2]
Пусть в некоторой окрестности точки
x
0
∈
R
{\displaystyle x_{0}\in \mathbb {R} }
функция
f
:
U
(
x
0
)
⊂
R
→
R
.
{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .}
A
{\displaystyle A}
U
(
x
0
)
{\displaystyle U(x_{0})}
f
(
x
0
+
h
)
=
f
(
x
0
)
+
A
h
+
o
(
h
)
{\displaystyle f(x_{0}+h)=f(x_{0})+Ah+o(h)}
если
A
{\displaystyle A}
предел Пусть в некоторой окрестности точки
x
0
∈
R
{\displaystyle x_{0}\in \mathbb {R} }
функция
f
:
U
(
x
0
)
⊂
R
→
R
.
{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
предел , если он существует,
f
′
(
x
0
)
=
lim
x
→
x
0
f
(
x
)
−
f
(
x
0
)
x
−
x
0
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
lim
Δ
x
→
0
Δ
f
(
x
)
Δ
x
.
{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim \limits _{{\Delta x}\to 0}{\frac {\Delta {f(x)}}{\Delta x}}.}
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
0
{\displaystyle x_{0}}
f
′
(
x
0
)
=
f
x
′
(
x
0
)
=
D
f
(
x
0
)
=
d
f
d
x
(
x
0
)
=
d
y
d
x
|
x
=
x
0
=
y
˙
(
x
0
)
.
{\displaystyle f'(x_{0})=f'_{x}(x_{0})=\mathrm {D} \!f(x_{0})={\frac {df}{dx}}(x_{0})=\left.{\frac {dy}{dx}}\right\vert _{x=x_{0}}={\dot {y}}(x_{0}).}
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике ).
Производные степенных функций
Производные тригонометрических функций
Производные обратных тригонометрических функций
(
c
)
′
=
0
{\displaystyle \left(c\right)'=0}
(
sin
x
)
′
=
cos
x
{\displaystyle \left(\sin x\right)'=\cos x}
(
arcsin
x
)
′
=
1
1
−
x
2
{\displaystyle \left(\arcsin x\right)'={\dfrac {1}{\sqrt {1-x^{2}}}}}
(
x
a
)
′
=
a
x
a
−
1
{\displaystyle \left(x^{a}\right)'=ax^{a-1}}
(
cos
x
)
′
=
−
sin
x
{\displaystyle \left(\cos x\right)'=-\sin x}
(
arccos
x
)
′
=
−
1
1
−
x
2
{\displaystyle \left(\arccos x\right)'=-{\dfrac {1}{\sqrt {1-x^{2}}}}}
(
a
x
)
′
=
a
x
ln
a
{\displaystyle \left(a^{x}\right)'=a^{x}\ln a}
(
tg
x
)
′
=
1
cos
2
x
{\displaystyle \left(\operatorname {tg} x\right)'={\dfrac {1}{\cos ^{2}x}}}
(
arctg
x
)
′
=
1
1
+
x
2
{\displaystyle \left(\operatorname {arctg} x\right)'={\dfrac {1}{1+x^{2}}}}
(
log
a
x
)
′
=
1
x
ln
a
{\displaystyle \left(\log _{a}x\right)'={\dfrac {1}{x\ln a}}}
(
ctg
x
)
′
=
−
1
sin
2
x
{\displaystyle \left(\operatorname {ctg} x\right)'=-{\dfrac {1}{\sin ^{2}x}}}
(
arcctg
x
)
′
=
−
1
1
+
x
2
{\displaystyle \left(\operatorname {arcctg} x\right)'=-{\dfrac {1}{1+x^{2}}}}
(
c
)
=
(
c
o
n
s
t
)
{\displaystyle \left(c\right)=\left(\mathrm {const} \right)}
(
e
x
)
(
n
)
=
e
x
{\displaystyle \left(e^{x}\right)^{\left(n\right)}=e^{x}}
Производная
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
∈
D
(
x
0
)
⇔
∃
f
′
(
x
0
)
∈
(
−
∞
;
∞
)
.
{\displaystyle f\in {\mathcal {D}}(x_{0})\Leftrightarrow \exists f'(x_{0})\in (-\infty ;\infty ).}
Для дифференцируемой в
x
0
{\displaystyle x_{0}}
f
{\displaystyle f}
U
(
x
0
)
{\displaystyle U(x_{0})}
f
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
o
(
x
−
x
0
)
{\displaystyle f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})}
x
→
x
0
.
{\displaystyle x\to x_{0}.}
Назовём
Δ
x
=
x
−
x
0
{\displaystyle \Delta x=x-x_{0}}
приращением аргумента функции, а
Δ
y
=
f
(
x
)
−
f
(
x
0
)
{\displaystyle \Delta y=f(x)-f(x_{0})}
Δ
y
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
{\displaystyle \Delta y=f(x_{0}+\Delta x)-f(x_{0})}
x
0
.
{\displaystyle x_{0}.}
f
′
(
x
0
)
=
lim
Δ
x
→
0
Δ
y
Δ
x
.
{\displaystyle f'(x_{0})=\lim \limits _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}.}
Пусть функция
f
:
(
a
,
b
)
→
R
{\displaystyle f\colon (a,b)\to \mathbb {R} }
x
0
∈
(
a
,
b
)
.
{\displaystyle x_{0}\in (a,b).}
произво́дная фу́нкция
f
′
:
(
a
,
b
)
→
R
.
{\displaystyle f'\colon (a,b)\to \mathbb {R} .}
Функция, имеющая производную в точке, непрерывна в ней. Обратное не всегда верно.
Если производная функция сама является непрерывной, то функцию
f
{\displaystyle f}
непреры́вно дифференци́руемой и пишут:
f
∈
C
(
1
)
(
(
a
,
b
)
)
.
{\displaystyle f\in C^{(1)}{\bigl (}(a,b){\bigr )}.}
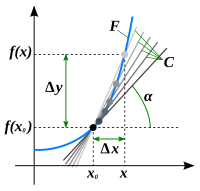
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0 ) . В окрестности точки x0 выбирается произвольная точка x . Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5 ). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1 ). Тангенс угла α наклона этой касательной — и есть производная в точке x0 . Если функция
f
:
U
(
x
0
)
→
R
{\displaystyle f\colon U(x_{0})\to \mathbb {R} }
x
0
,
{\displaystyle x_{0},}
U
(
x
0
)
{\displaystyle U(x_{0})}
линейной функцией
f
l
(
x
)
≡
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
.
{\displaystyle f_{l}(x)\equiv f(x_{0})+f'(x_{0})(x-x_{0}).}
Функция
f
l
{\displaystyle f_{l}}
f
{\displaystyle f}
x
0
.
{\displaystyle x_{0}.}
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
угловым коэффициентом тангенсом угла наклона касательной прямой.
Пусть
s
=
s
(
t
)
{\displaystyle s=s(t)}
движения . Тогда
v
(
t
0
)
=
s
′
(
t
0
)
{\displaystyle v(t_{0})=s'(t_{0})}
мгновенную скорость движения в момент времени
t
0
.
{\displaystyle t_{0}.}
a
(
t
0
)
=
s
″
(
t
0
)
{\displaystyle a(t_{0})=s''(t_{0})}
мгновенное ускорение в момент времени
t
0
.
{\displaystyle t_{0}.}
Вообще производная функции
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
0
{\displaystyle x_{0}}
x
0
{\displaystyle x_{0}}
процесса , описанного зависимостью
y
=
f
(
x
)
.
{\displaystyle y=f(x).}
Анимация, дающая первоначальное интуитивное представление о производной, как "размах" изменения функции при изменении аргумента (нажмите для воспроизведения).
Понятие производной произвольного порядка задаётся рекуррентно . Полагаем
f
(
0
)
(
x
0
)
≡
f
(
x
0
)
.
{\displaystyle f^{(0)}(x_{0})\equiv f(x_{0}).}
Если функция
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
(
1
)
(
x
0
)
≡
f
′
(
x
0
)
.
{\displaystyle f^{(1)}(x_{0})\equiv f'(x_{0}).}
Пусть теперь производная
n
{\displaystyle n}
f
(
n
)
{\displaystyle f^{(n)}}
x
0
{\displaystyle x_{0}}
f
(
n
+
1
)
(
x
0
)
=
(
f
(
n
)
)
′
(
x
0
)
.
{\displaystyle f^{(n+1)}(x_{0})=\left(f^{(n)}\right)'(x_{0}).}
Если функция
u
=
f
(
x
,
y
,
z
)
{\displaystyle u=f(x,y,z)}
частную производную по одной из переменных, то названная производная, сама являясь функцией от
x
,
y
,
z
,
{\displaystyle x,y,z,}
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
u
=
f
(
x
,
y
,
z
)
{\displaystyle u=f(x,y,z)}
u
x
2
″
=
f
x
2
″
(
x
0
,
y
0
,
z
0
)
{\displaystyle u''_{x^{2}}=f''_{x^{2}}(x_{0},y_{0},z_{0})}
∂
2
u
∂
x
2
=
∂
2
f
(
x
0
,
y
0
,
z
0
)
∂
x
2
{\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x^{2}}}}
u
x
y
″
=
f
x
y
″
(
x
0
,
y
0
,
z
0
)
{\displaystyle u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})}
∂
2
u
∂
x
∂
y
=
∂
2
f
(
x
0
,
y
0
,
z
0
)
∂
x
∂
y
{\displaystyle {\frac {\partial ^{2}u}{\partial x\partial y}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x\partial y}}}
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной . Например,
u
x
y
″
=
f
x
y
″
(
x
0
,
y
0
,
z
0
)
{\displaystyle u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})}
Класс функций, у которых производная
n
{\displaystyle n}
C
(
n
)
{\displaystyle C^{(n)}}
В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:
Лагранжа
f
(
n
)
(
x
0
)
{\displaystyle f^{(n)}(x_{0})}
f
(
1
)
(
x
0
)
=
f
′
(
x
0
)
=
f
I
(
x
0
)
,
{\displaystyle f^{(1)}(x_{0})=f'(x_{0})=f^{I}(x_{0}),}
f
(
2
)
(
x
0
)
=
f
″
(
x
0
)
=
f
I
I
(
x
0
)
,
{\displaystyle f^{(2)}(x_{0})=f''(x_{0})=f^{II}(x_{0}),}
f
(
3
)
(
x
0
)
=
f
‴
(
x
0
)
=
f
I
I
I
(
x
0
)
,
{\displaystyle f^{(3)}(x_{0})=f'''(x_{0})=f^{III}(x_{0}),}
f
(
4
)
(
x
0
)
=
f
I
V
(
x
0
)
,
{\displaystyle f^{(4)}(x_{0})=f^{IV}(x_{0}),}
Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.
Лейбница , удобная наглядной записью отношения бесконечно малых (только в случае, если
x
{\displaystyle x}
d
n
f
d
x
n
(
x
0
)
{\displaystyle {\frac {d^{n}\!f}{dx^{n}}}(x_{0})}
Ньютона , которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:
x
˙
(
t
0
)
{\displaystyle {\dot {x}}(t_{0})}
x
{\displaystyle x}
t
{\displaystyle t}
t
=
t
0
{\displaystyle t=t_{0}}
f
¨
(
x
0
)
{\displaystyle {\ddot {f}}(x_{0})}
f
{\displaystyle f}
x
{\displaystyle x}
x
0
{\displaystyle x_{0}}
D
n
f
(
x
0
)
{\displaystyle \mathrm {D} ^{n}\!f(x_{0})}
∂
n
f
(
x
0
)
{\displaystyle \partial ^{n}\!f(x_{0})}
В вариационном исчислении и математической физике часто применяется обозначение
f
x
{\displaystyle f_{x}}
f
x
x
{\displaystyle f_{xx}}
f
x
|
x
=
x
0
{\displaystyle f_{x}\vert _{x=x_{0}}}
Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:
f
(
n
)
(
x
0
)
=
d
n
f
d
x
n
(
x
0
)
=
f
⋅
⋅
.
.
.
⋅
⏞
n
P
A
3
(
x
0
)
=
D
n
f
(
x
0
)
=
f
x
x
…
x
⏟
n
P
A
3
|
x
=
x
0
.
{\displaystyle f^{(n)}(x_{0})={\frac {d^{n}\!f}{dx^{n}}}(x_{0})={\overset {\overbrace {\cdot \cdot ...\cdot } ^{n\ \mathrm {PA} 3}}{f}}(x_{0})=\mathrm {D} ^{n}\!f(x_{0})=f{\underbrace {_{xx\ldots x}} _{n\ \mathrm {PA} 3}}\vert _{x=x_{0}}.}
Пусть
f
(
x
)
=
x
2
{\displaystyle f(x)=x^{2}}
f
′
(
x
0
)
=
lim
x
→
x
0
x
2
−
x
0
2
x
−
x
0
=
lim
x
→
x
0
(
x
−
x
0
)
(
x
+
x
0
)
x
−
x
0
=
lim
x
→
x
0
(
x
+
x
0
)
=
2
x
0
.
{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {x^{2}-x_{0}^{2}}{x-x_{0}}}=\lim \limits _{x\to x_{0}}{\frac {(x-x_{0})(x+x_{0})}{x-x_{0}}}=\lim \limits _{x\to x_{0}}(x+x_{0})=2x_{0}.}
Пусть
f
(
x
)
=
|
x
|
{\displaystyle f(x)=|x|}
x
0
≠
0
,
{\displaystyle x_{0}\neq 0,}
f
′
(
x
0
)
=
sgn
x
0
,
{\displaystyle f'(x_{0})=\operatorname {sgn} x_{0},}
где
sgn
{\displaystyle \operatorname {sgn} }
функцию знака . А если
x
0
=
0
,
{\displaystyle x_{0}=0,}
f
+
′
(
x
0
)
=
1
,
f
−
′
(
x
0
)
=
−
1
,
{\displaystyle f'_{+}(x_{0})=1,\;f'_{-}(x_{0})=-1,}
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если
C
{\displaystyle C}
f
=
f
(
x
)
,
g
=
g
(
x
)
{\displaystyle f=f(x),g=g(x)}
правила дифференцирования:
C
′
=
0
{\displaystyle C'=0}
x
′
=
1
{\displaystyle x'=1}
(
f
+
g
)
′
=
f
′
+
g
′
{\displaystyle \left(f+g\right)'=f'+g'}
[ 3]
y
(
x
)
=
f
(
x
)
+
g
(
x
)
{\displaystyle y(x)=f(x)+g(x)}
y
′
(
x
)
=
lim
Δ
x
→
0
y
(
x
+
Δ
x
)
−
y
(
x
)
Δ
x
=
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta {x})-y(x)}{\Delta x}}=}
=
lim
Δ
x
→
0
(
f
(
x
+
Δ
x
)
+
g
(
x
+
Δ
x
)
)
−
(
f
(
x
)
+
g
(
x
)
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {(f(x+\Delta {x})+g(x+\Delta {x}))-(f(x)+g(x))}{\Delta x}}=}
=
lim
Δ
x
→
0
(
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
+
g
(
x
+
Δ
x
)
−
g
(
x
)
Δ
x
)
=
{\displaystyle =\lim _{\Delta x\to 0}{({\frac {f(x+\Delta x)-f(x)}{\Delta x}}+{\frac {g(x+\Delta x)-g(x)}{\Delta x}})}=}
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
+
lim
Δ
x
→
0
g
(
x
+
Δ
x
)
−
g
(
x
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}+\lim _{\Delta x\to 0}{\frac {g(x+\Delta x)-g(x)}{\Delta x}}=}
=
f
′
(
x
)
+
g
′
(
x
)
{\displaystyle =f'(x)+g'(x)}
■
(
f
g
)
′
=
f
′
g
+
f
g
′
{\displaystyle \left(fg\right)'=f'g+fg'}
[ 4]
y
(
x
)
=
f
(
x
)
g
(
x
)
{\displaystyle y(x)=f(x)g(x)}
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta f(x)=f(x+\Delta x)-f(x)}
Δ
g
(
x
)
=
g
(
x
+
Δ
x
)
−
g
(
x
)
{\displaystyle \Delta g(x)=g(x+\Delta x)-g(x)}
y
′
(
x
)
=
lim
Δ
x
→
0
y
(
x
+
Δ
x
)
−
y
(
x
)
Δ
x
=
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta x)-y(x)}{\Delta x}}=}
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
g
(
x
+
Δ
x
)
−
f
(
x
)
g
(
x
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)g(x+\Delta x)-f(x)g(x)}{\Delta x}}=}
=
lim
Δ
x
→
0
(
f
(
x
)
+
Δ
f
(
x
)
)
(
g
(
x
)
+
Δ
g
(
x
)
)
−
f
(
x
)
g
(
x
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {(f(x)+\Delta f(x))(g(x)+\Delta g(x))-f(x)g(x)}{\Delta x}}=}
=
lim
Δ
x
→
0
f
(
x
)
g
(
x
)
+
f
(
x
)
Δ
g
(
x
)
+
Δ
f
(
x
)
g
(
x
)
+
Δ
f
(
x
)
Δ
g
(
x
)
−
f
(
x
)
g
(
x
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x)g(x)+f(x)\Delta g(x)+\Delta f(x)g(x)+\Delta f(x)\Delta g(x)-f(x)g(x)}{\Delta x}}=}
=
lim
Δ
x
→
0
(
f
(
x
)
Δ
g
(
x
)
Δ
x
+
g
(
x
)
Δ
f
(
x
)
Δ
x
+
Δ
g
(
x
)
Δ
f
(
x
)
Δ
x
)
=
{\displaystyle =\lim _{\Delta x\to 0}(f(x){\frac {\Delta g(x)}{\Delta x}}+g(x){\frac {\Delta f(x)}{\Delta x}}+\Delta g(x){\frac {\Delta f(x)}{\Delta x}})=}
=
f
(
x
)
g
′
(
x
)
+
g
(
x
)
f
′
(
x
)
+
0
f
′
(
x
)
=
{\displaystyle =f(x)g'(x)+g(x)f'(x)+0f'(x)=}
=
f
′
(
x
)
g
(
x
)
+
f
(
x
)
g
′
(
x
)
{\displaystyle =f'(x)g(x)+f(x)g'(x)}
■
(
C
f
)
′
=
C
f
′
{\displaystyle \left(Cf\right)'=Cf'}
(
f
g
)
′
=
f
′
g
−
f
g
′
g
2
{\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}
≠ 0)
y
(
x
)
=
f
(
x
)
g
(
x
)
{\displaystyle y(x)={\frac {f(x)}{g(x)}}}
Δ
f
(
x
)
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta f(x)=f(x+\Delta x)-f(x)}
Δ
g
(
x
)
=
g
(
x
+
Δ
x
)
−
g
(
x
)
{\displaystyle \Delta g(x)=g(x+\Delta x)-g(x)}
y
′
(
x
)
=
lim
Δ
x
→
0
y
(
x
+
Δ
x
)
−
y
(
x
)
Δ
x
=
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta x)-y(x)}{\Delta x}}=}
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
g
(
x
+
Δ
x
)
−
f
(
x
)
g
(
x
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {{\frac {f(x+\Delta x)}{g(x+\Delta x)}}-{\frac {f(x)}{g(x)}}}{\Delta x}}=}
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
g
(
x
)
−
f
(
x
)
g
(
x
+
Δ
x
)
g
(
x
+
Δ
x
)
g
(
x
)
Δ
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)g(x)-f(x)g(x+\Delta x)}{g(x+\Delta x)g(x)\Delta x}}=}
=
1
g
2
(
x
)
lim
Δ
x
→
0
(
f
(
x
)
+
Δ
f
(
x
)
)
g
(
x
)
−
f
(
x
)
(
g
(
x
)
+
Δ
g
(
x
)
)
Δ
x
=
{\displaystyle ={\frac {1}{g^{2}(x)}}\lim _{\Delta x\to 0}{\frac {(f(x)+\Delta f(x))g(x)-f(x)(g(x)+\Delta g(x))}{\Delta x}}=}
=
1
g
2
(
x
)
lim
Δ
x
→
0
f
(
x
)
g
(
x
)
+
Δ
f
(
x
)
g
(
x
)
−
f
(
x
)
g
(
x
)
−
f
(
x
)
Δ
g
(
x
)
Δ
x
=
{\displaystyle ={\frac {1}{g^{2}(x)}}\lim _{\Delta x\to 0}{\frac {f(x)g(x)+\Delta f(x)g(x)-f(x)g(x)-f(x)\Delta g(x)}{\Delta x}}=}
=
1
g
2
(
x
)
lim
Δ
x
→
0
(
g
(
x
)
Δ
f
(
x
)
Δ
x
−
f
(
x
)
Δ
g
(
x
)
Δ
x
)
=
{\displaystyle ={\frac {1}{g^{2}(x)}}\lim _{\Delta x\to 0}{(g(x){\frac {\Delta f(x)}{\Delta x}}-f(x){\frac {\Delta g(x)}{\Delta x}})}=}
=
1
g
2
(
x
)
(
g
(
x
)
f
′
(
x
)
−
f
(
x
)
g
′
(
x
)
)
=
{\displaystyle ={\frac {1}{g^{2}(x)}}(g(x)f'(x)-f(x)g'(x))=}
=
f
′
(
x
)
g
(
x
)
−
f
(
x
)
g
′
(
x
)
g
2
(
x
)
{\displaystyle ={\frac {f'(x)g(x)-f(x)g'(x)}{g^{2}(x)}}}
■
(
C
g
)
′
=
−
C
g
′
g
2
{\displaystyle \left({\frac {C}{g}}\right)'=-{\frac {Cg'}{g^{2}}}}
≠ 0)Если функция задана параметрически:
{
x
=
x
(
t
)
,
y
=
y
(
t
)
,
t
∈
[
T
1
;
T
2
]
{\displaystyle \left\{{\begin{matrix}x=x(t),\\y=y(t),\end{matrix}}\;\;t\in \left[T_{1};T_{2}\right]\right.}
y
x
′
=
d
y
d
x
=
d
y
d
t
⋅
d
t
d
x
=
y
t
′
⋅
t
x
′
=
y
t
′
x
t
′
{\displaystyle y'_{x}={\frac {dy}{dx}}={\frac {dy}{dt}}\cdot {\frac {dt}{dx}}=y'_{t}\cdot t'_{x}={\frac {y'_{t}}{x'_{t}}}}
d
d
x
f
(
g
(
x
)
)
=
d
f
(
g
)
d
g
⋅
d
g
(
x
)
d
x
=
f
g
′
g
x
′
{\displaystyle {\frac {d}{dx}}f(g(x))={\frac {df(g)}{dg}}\cdot {\frac {dg(x)}{dx}}=f'_{g}g'_{x}}
Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница ):
(
f
g
)
(
n
)
=
∑
k
=
0
n
C
n
k
f
(
n
−
k
)
g
(
k
)
,
{\displaystyle (fg)^{(n)}=\sum \limits _{k=0}^{n}{C_{n}^{k}f^{(n-k)}g^{(k)}},}
C
n
k
{\displaystyle C_{n}^{k}}
биномиальные коэффициенты .Следующие свойства производной служат дополнением к правилам дифференцирования:
если функция дифференцируема на интервале
(
a
,
b
)
{\displaystyle (a,b)}
(
a
,
b
)
{\displaystyle (a,b)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
[
−
1
,
1
]
{\displaystyle [-1,1]}
если функция имеет локальный максимум/минимум при значении аргумента, равном
x
{\displaystyle x}
f
′
(
x
)
=
0
{\displaystyle f'(x)=0}
лемма Ферма );
производная данной функции единственна, но у разных функций могут быть одинаковые производные.
(
f
(
x
)
g
(
x
)
)
′
=
f
(
x
)
g
(
x
)
(
g
′
(
x
)
ln
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
)
(
∀
x
∈
D
f
:
f
(
x
)
>
0
)
{\displaystyle (f(x)^{g(x)})'=f(x)^{g(x)}\left(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}\right)(\forall x\in D_{f}:f(x)>0)}
y
=
f
(
x
)
g
(
x
)
{\displaystyle y=f(x)^{g(x)}}
ln
y
=
g
(
x
)
ln
f
(
x
)
{\displaystyle \ln y=g(x)\ln f(x)}
y
′
y
=
g
′
(
x
)
ln
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
{\displaystyle {\frac {y'}{y}}=g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}}
y
′
=
y
(
g
′
(
x
)
ln
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
)
{\displaystyle y'=y\left(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}\right)}
y
′
=
f
(
x
)
g
(
x
)
(
g
′
(
x
)
ln
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
)
{\displaystyle y'=f(x)^{g(x)}(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}})}
■
Функция
f
(
x
)
{\displaystyle f(x)}
Производная
f
′
(
x
)
{\displaystyle f'(x)}
Примечание
x
α
{\displaystyle x^{\alpha }}
α
⋅
x
α
−
1
{\displaystyle \alpha \cdot x^{\alpha -1}}
Фиксируем
x
∈
D
(
f
)
{\displaystyle x\in \mathbb {D} (f)}
Δ
x
{\displaystyle \Delta x}
Δ
y
=
(
x
+
Δ
x
)
α
−
x
α
=
x
α
(
(
1
+
Δ
x
x
)
α
−
1
)
{\displaystyle \Delta y=(x+\Delta x)^{\alpha }-x^{\alpha }=x^{\alpha }((1+{\frac {\Delta x}{x}})^{\alpha }-1)}
(
x
α
)
′
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
x
→
0
x
α
(
(
1
+
Δ
x
x
)
α
−
1
)
Δ
x
=
{\displaystyle (x^{\alpha })'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {x^{\alpha }((1+{\frac {\Delta x}{x}})^{\alpha }-1)}{\Delta x}}=}
См.
=
lim
Δ
x
→
0
α
⋅
x
α
⋅
Δ
x
x
Δ
x
=
α
⋅
x
α
−
1
{\displaystyle =\lim _{\Delta x\to 0}{\frac {\alpha \cdot x^{\alpha }\cdot {\frac {\Delta x}{x}}}{\Delta x}}=\alpha \cdot x^{\alpha -1}}
a
x
{\displaystyle a^{x}}
a
x
⋅
ln
a
{\displaystyle a^{x}\cdot \ln {a}}
Фиксируем
x
∈
D
(
f
)
{\displaystyle x\in \mathbb {D} (f)}
Δ
x
{\displaystyle \Delta x}
Δ
y
=
a
x
+
Δ
x
−
a
x
=
a
x
(
a
Δ
x
−
1
)
{\displaystyle \Delta y=a^{x+\Delta x}-a^{x}=a^{x}(a^{\Delta x}-1)}
(
a
x
)
′
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
x
→
0
a
x
(
a
Δ
x
−
1
)
Δ
x
=
{\displaystyle (a^{x})'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {a^{x}(a^{\Delta x}-1)}{\Delta x}}=}
См.
=
lim
Δ
x
→
0
a
x
⋅
Δ
x
⋅
ln
a
Δ
x
=
a
x
⋅
ln
a
{\displaystyle =\lim _{\Delta x\to 0}{\frac {a^{x}\cdot \Delta x\cdot \ln {a}}{\Delta x}}=a^{x}\cdot \ln {a}}
log
a
x
{\displaystyle \log _{a}{x}}
1
x
⋅
ln
a
{\displaystyle {\frac {1}{x\cdot \ln {a}}}}
sin
x
{\displaystyle \sin x}
cos
x
{\displaystyle \cos x}
cos
x
{\displaystyle \cos x}
−
sin
x
{\displaystyle -\sin x}
t
g
x
{\displaystyle \mathrm {tg} \ x}
1
cos
2
x
{\displaystyle {\frac {1}{\cos ^{2}{x}}}}
c
t
g
x
{\displaystyle \mathrm {ctg} \ x}
−
1
sin
2
x
{\displaystyle -{\frac {1}{\sin ^{2}{x}}}}
arcsin
x
{\displaystyle \arcsin {x}}
1
1
−
x
2
{\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}}
arccos
x
{\displaystyle \arccos {x}}
−
1
1
−
x
2
{\displaystyle -{\frac {1}{\sqrt {1-x^{2}}}}}
a
r
c
t
g
x
{\displaystyle \mathrm {arctg} \ x}
1
1
+
x
2
{\displaystyle {\frac {1}{1+x^{2}}}}
a
r
c
c
t
g
x
{\displaystyle \mathrm {arcctg} \ x}
−
1
1
+
x
2
{\displaystyle -{\frac {1}{1+x^{2}}}}
s
h
x
{\displaystyle \mathrm {sh} \ x}
c
h
x
{\displaystyle \mathrm {ch} \ x}
c
h
x
{\displaystyle \mathrm {ch} \ x}
s
h
x
{\displaystyle \mathrm {sh} \ x}
t
h
x
{\displaystyle \mathrm {th} \ x}
1
c
h
2
x
{\displaystyle {\frac {1}{\mathrm {ch} ^{2}\ x}}}
c
t
h
x
{\displaystyle \mathrm {cth} \ x}
−
1
s
h
2
x
{\displaystyle -{\frac {1}{\mathrm {sh} ^{2}\ x}}}
Определим производную вектор-функции
r
(
t
)
{\displaystyle \mathbf {r} (t)}
d
d
t
r
(
t
)
=
lim
h
→
0
r
(
t
+
h
)
−
r
(
t
)
h
{\displaystyle {\frac {d}{dt}}\mathbf {r} (t)=\lim _{h\to 0}{\frac {\mathbf {r} (t+h)-\mathbf {r} (t)}{h}}}
Если производная в точке
t
{\displaystyle t}
x
′
(
t
)
,
y
′
(
t
)
,
z
′
(
t
)
{\displaystyle x'(t),\ y'(t),\ z'(t)}
Свойства производной вектор-функции (всюду предполагается, что производные существуют):
d
d
t
(
r
1
(
t
)
+
r
2
(
t
)
)
=
d
r
1
(
t
)
d
t
+
d
r
2
(
t
)
d
t
{\displaystyle {\frac {d}{dt}}(\mathbf {r_{1}} (t)+\mathbf {r_{2}} (t))={\frac {d\mathbf {r_{1}} (t)}{dt}}+{\frac {d\mathbf {r_{2}} (t)}{dt}}}
d
d
t
(
f
(
t
)
r
(
t
)
)
=
d
f
(
t
)
d
t
r
(
t
)
+
f
(
t
)
d
r
(
t
)
d
t
{\displaystyle {\frac {d}{dt}}(f(t)\mathbf {r} (t))={\frac {df(t)}{dt}}\mathbf {r} (t)+f(t){\frac {d\mathbf {r} (t)}{dt}}}
f
(
t
)
{\displaystyle f(t)}
d
d
t
(
r
1
(
t
)
r
2
(
t
)
)
=
d
r
1
(
t
)
d
t
r
2
(
t
)
+
r
1
(
t
)
d
r
2
(
t
)
d
t
{\displaystyle {\frac {d}{dt}}(\mathbf {r_{1}} (t)\mathbf {r_{2}} (t))={\frac {d\mathbf {r_{1}} (t)}{dt}}\mathbf {r_{2}} (t)+\mathbf {r_{1}} (t){\frac {d\mathbf {r_{2}} (t)}{dt}}}
скалярного произведения .
d
d
t
[
r
1
(
t
)
,
r
2
(
t
)
]
=
[
d
r
1
(
t
)
d
t
,
r
2
(
t
)
]
+
[
r
1
(
t
)
,
d
r
2
(
t
)
d
t
]
{\displaystyle {\frac {d}{dt}}[\mathbf {r_{1}} (t),\mathbf {r_{2}} (t)]=\left[{\frac {d\mathbf {r_{1}} (t)}{dt}},\mathbf {r_{2}} (t)\right]+\left[\mathbf {r_{1}} (t),{\frac {d\mathbf {r_{2}} (t)}{dt}}\right]}
векторного произведения .
d
d
t
(
a
(
t
)
,
b
(
t
)
,
c
(
t
)
)
=
(
d
a
(
t
)
d
t
,
b
(
t
)
,
c
(
t
)
)
+
(
a
(
t
)
,
d
b
(
t
)
d
t
,
c
(
t
)
)
+
(
a
(
t
)
,
b
(
t
)
,
d
c
(
t
)
d
t
)
{\displaystyle {\frac {d}{dt}}(\mathbf {a} (t),\mathbf {b} (t),\mathbf {c} (t))=\left({\frac {d\mathbf {a} (t)}{dt}},\mathbf {b} (t),\mathbf {c} (t)\right)+\left(\mathbf {a} (t),{\frac {d\mathbf {b} (t)}{dt}},\mathbf {c} (t)\right)+\left(\mathbf {a} (t),\mathbf {b} (t),{\frac {d\mathbf {c} (t)}{dt}}\right)}
смешанного произведения .
D
x
q
f
(
x
)
=
f
(
q
x
)
−
f
(
x
)
(
q
−
1
)
x
.
{\displaystyle D_{x}^{q}f(x)={\frac {f(qx)-f(x)}{(q-1)x}}.}
↑ Колмогоров А. Н. , Абрамов А. М. , Дудницын Ю. П.ISBN 5-09-006088-6 . - C. 155-156↑ Комков Г. Д. , Левшин Б. В., Семенов Л. К.М. : Наука , 1977. — Т. 1. 1724—1917. — С. 173.↑ Производная суммы равна сумме производных
↑ Отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу
↑ A.I. Olemskoi, S.S. Borysov,a, and I.A. Shuda. Statistical field theories deformed within different calculi
Виленкин Н., Мордкович А. Что такое производная // Квант. — 1975. — № 12 .В. Г. Болтянский ,«Популярные лекции по математике» , Выпуск 17, Гостехиздат 1955 г., 64 стр.В. А. Гусев , А. Г. Мордкович «Математика»Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1В. М. Бородихин , Высшая математика , учеб. пособие, ISBN 5-7782-0422-1























































































































![{\displaystyle \left\{{\begin{matrix}x=x(t),\\y=y(t),\end{matrix}}\;\;t\in \left[T_{1};T_{2}\right]\right.}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/66c1512a040f80645b424f10cb2fc237be942c83)






![{\displaystyle [-1,1]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)



















































![{\displaystyle {\frac {d}{dt}}[\mathbf {r_{1}} (t),\mathbf {r_{2}} (t)]=\left[{\frac {d\mathbf {r_{1}} (t)}{dt}},\mathbf {r_{2}} (t)\right]+\left[\mathbf {r_{1}} (t),{\frac {d\mathbf {r_{2}} (t)}{dt}}\right]}](https://wikimedia.org/ruwiki/api/rest_v1/media/math/render/svg/0b172aa52700f4bc10de3dc186111a82e2465a50)

