Теорема Мендельсона — Далмейджа

В теории графов теорема Мендельсона-Далмейджа (Далмеджа) описывает важное свойство паросочетаний в двудольных графах. Теорема доказана Н. С. Мендельсоном и А. Л. Далмейджом в 1958 году. Следствие из теоремы даёт один из алгоритмов построения оптимальной рёберной раскраски двудольного графа (или, что то же самое, разбиения множества рёбер двудольного графа на наименьшее число паросочетаний).

Определения

Граф называется двудольным, если его вершины можно разбить на множества $X$ и $Y$ так, чтобы любое ребро соединяло вершину из множества $X$ с вершиной из множества $Y$. Такие графы обычно обозначаются $G=(X,Y,E)$, где $E$ — множество рёбер графа. Множество $X$ называют левой долей графа, а множество $Y$ — правой долей графа.

Паросочетанием в графе называется множество рёбер, не имеющих общих конечных вершин.

Говорят, что паросочетание $M$ насыщает подмножество вершин левой (или, соответственно, правой) доли, если для любой вершины в этом подмножестве существует ребро из $M$, которое инцидентно этой вершине.

Утверждение теоремы

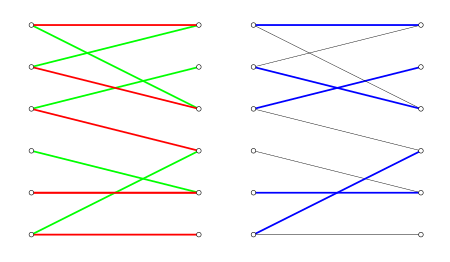
Пусть $G=(X,Y,E)$ — двудольный граф, в котором обозначены подмножества вершин $X_{1}\subseteq X$ и $Y_{2}\subseteq Y$. Если существуют паросочетания $M_{1}$ и $M_{2}$ такие, что $M_{1}$ насыщает $X_{1}$, а $M_{2}$ насыщает $Y_{2}$, то существует паросочетание $M$, которое насыщает одновременно множества $X_{1}$ и $M_{2}$.

Пример

На рисунке изображены паросочетания $M_{1}$ (красное), $M_{2}$ (зелёное) и $M$ (синее) из утверждения теоремы. Паросочетание $M_{1}$ насыщает множество $X_{1}=\{x_{1},x_{2},x_{3},x_{5},x_{6}\}$ (вершины на рисунке пронумерованы сверху вниз). Паросочетание $M_{2}$ насыщает множество $Y_{2}=\{y_{1},y_{2},y_{3},y_{4},y_{5}\}$. Паросочетание $M$ насыщает оба этих множества.

Следствия

Следствие 1

В двудольном графе существует паросочетание, насыщающее все вершины максимальной степени.

Доказательство. Пусть максимальная степень вершины в двудольном графе равняется $\Delta$. Возьмём в качестве множества $X_{1}$ все вершины левой доли со степенью $\Delta$, а в качестве множества $Y_{2}$ — все вершины правой доли со степенью $\Delta$ (одно из множеств $X_{1}$ и $Y_{2}$ может быть и пустым). Из теоремы Холла следует, что существуют паросочетания $M_{1}$ и $M_{2}$, насыщающие множества $X_{1}$ и $Y_{2}$ соответственно. Значит, по теореме Мендельсона-Далмейджа, существует и паросочетание $M$, насыщающее все вершины степени $\Delta$.

Следствие 2

Множество рёбер двудольного графа с максимальной степенью вершины $\Delta$ можно разбить на $\Delta$ паросочетаний, или, иными словами, для рёберной раскраски этого графа необходимо и достаточно $\Delta$ цветов (этот результат впервые получен Кёнигом).

Доказательство. Рассмотрим все вершины степени $\Delta$. По следствию 1, в графе существует паросочетание, насыщающее их все. Удалив из графа все рёбра этого паросочетания, получим граф с максимальной степенью вершин $\Delta -1$. Повторим для него ту же процедуру, и так далее. В итоге будут построены $\Delta$ паросочетаний, а в графе больше не останется рёбер.

Алгоритм и вычислительная сложность

Доказательство теоремы Мендельсона-Далмейджа и следствий из неё представляет собой алгоритм разбиения рёбер двудольного графа на наименьшее число паросочетаний.

Алгоритм выполняет $\Delta$ шагов, на каждом нужно построить паросочетания $M_{1}$ и $M_{2}$ (это можно сделать алгоритмом Хопкрофта-Карпа за время $O(|E|{\sqrt {|V|}})$) и паросочетание $M$ (это можно сделать за время $O(|E|)$). Итоговая сложность работы алгоритма — $O(\Delta |E|{\sqrt {|V|}})$.

Ссылки

• Mendelsohn, N. S., Dulmage, A. L. Some Generalizations of the Problem of Distinct Representatives // Canadian Journal of Mathematics. — 1958. — Vol. 10. — P. 230-241.

• Свами М., Тхуласираман К. Графы, сети и алгоритмы. — М.: Мир, 1984. — 455 с. — ISBN 978-5-458-33391-7.

• Kőnig, D. Uber Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre // Mathematische Annalen. — 1916. — Т. 77, вып. 4. — С. 453—465. — doi:10.1007/BF01456961.