Потенциал Сазерленда

Потенциал Сазерленда (Sutherland potential) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния $r$ между ними. Впервые этот вид потенциала был предложен Уильямом Сазерлендом в 1893 году. Потенциал сочетает в себе твердую сердцевину (бесконечно высокое отталкивание на близких расстояниях) с притягивающим хвостом, описываемым степенным законом. Эта модель относительно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании.

Вид потенциала взаимодействия

Характерный вид потенциала Сазерленда

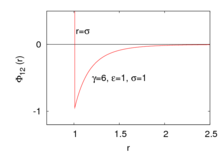
Уильям Сазерленд получил более реалистичное выражение для потенциала взаимодействия, чем полученное из потенциала бесконечно жестких упругих сфер. Данный потенциал описывается следующим выражением:

$\Phi _{2}(r)={\begin{cases}\infty ,{\phantom {mmm,}}r\leq \sigma \\-\varepsilon \left({\dfrac {\sigma }{r}}\right)^{\gamma },r>\sigma \end{cases}},$

где $\Phi _{2}(r)$ — потенциал парного взаимодействия, $r=|{\boldsymbol {r_{1}}}-{\boldsymbol {r_{2}}}|$ — расстояние между частицами 1 и 2, положение которых описывается радиусом-вектором ${\boldsymbol {r}}$. $\varepsilon$ — глубина потенциальной ямы, $\sigma$ — радиус соответствующей твёрдой сферы, $\gamma$ — параметр, контроллирующий скорость убывания потенциала до нуля.

Данный потенциал, в отличие от потенциала Леннарда-Джонса, является «притягивательным», то есть описывающим лишь притяжение частиц в силу того, что на больших расстояниях $F_{2}=-{\frac {{\text{d}}\Phi _{2}(r)}{{\text{d}}r}}\leq 0$. Отталкивание частиц происходит лишь на расстояниях, $r\leq \sigma$ с бесконечной силой.

Вириальные коэффициенты

Вид второго вириального коэффициента при $\gamma =6$. Пунктирная линия — касательная к графику.

Коэффициенты разложения третьего вириального коэффициента

Коэффициент	Значение коэффициента
$c_{0}$	0.625
$c_{1}$	-0.6448603
$c_{2}$	0.2861417
$c_{3}$	0.0709195
$c_{4}$	0.0027382
$c_{5}$	-0.0062834
$c_{6}$	-0.0035694
$c_{7}$	-0.0013018
$c_{8}$	-0.0003808
$c_{9}$	-0.0000961
$c_{10}$	-0.0000217

Второй вириальный коэффициент

Второй вириальный коэффициент данного потенциала можно выразить в следующем виде

$B_{2}(\tau )=-2\pi \sigma ^{3}\sum _{n=0}^{\infty }{\frac {\tau ^{-n}}{n!(n\gamma -3)}}=-{\frac {2\pi \sigma ^{3}}{\gamma }}\left(-{\frac {1}{\tau }}\right)^{3/\gamma }\Gamma \left(-{\frac {3}{\gamma }},0,-{\frac {1}{\tau }}\right)$

где $\tau =kT/\varepsilon$ — приведённая температура, а $\Gamma (a,z_{0},z_{1})$ — обобщённая неполная гамма-функция: $\Gamma (a,z_{0},z_{1})=\Gamma (a,z_{0})-\Gamma (a,z_{1})$

Вывод выражения второго вириального коэффициента

Как известно, в общем виде второй вириальный коэффициент можно записать как

$B_{2}(T)=-2\pi \int _{0}^{\infty }r^{2}\left(\exp \left[-{\frac {\Phi _{ij}(r)}{kT}}\right]-1\right)dr$

Подставим выражение потенциала Сазерленда

$B_{2}(T)=-2\pi \int _{0}^{\infty }r^{2}\left(\exp \left[-{\frac {\Phi _{ij}(r)}{kT}}\right]-1\right)dr=2\pi \int _{0}^{\sigma }r^{2}dr-2\pi \int _{\sigma }^{\infty }r^{2}\left(\exp \left[{\frac {\varepsilon }{kT}}\left({\frac {\sigma }{r}}\right)^{\gamma }\right]-1\right)dr={\frac {2}{3}}\pi \sigma ^{3}-2\pi \int _{\sigma }^{\infty }r^{2}\left(\exp \left[{\frac {\varepsilon }{kT}}\left({\frac {\sigma }{r}}\right)^{\gamma }\right]-1\right)dr$

Сделаем подстановку $x=r/\sigma$ и $\tau =kT/\varepsilon$

$B_{2}(\tau )/{\frac {2}{3}}\pi \sigma ^{3}=1-3\int _{1}^{\infty }x^{2}\left(\exp \left[{\frac {1}{\tau x^{\gamma }}}\right]-1\right)dx$

Разложим экспоненту в ряд по степеням $1/\tau$ и почленно проинтегрируем

$B_{2}(\tau )/{\frac {2}{3}}\pi \sigma ^{3}=1-3\sum \limits _{n=1}^{\infty }{\frac {\tau ^{-n}}{n!(\gamma n-3)}}=-3\sum \limits _{n=0}^{\infty }{\frac {\tau ^{-n}}{n!(\gamma n-3)}}$

В результате получим, что второй вириальный коэффициент данного потенциала можно выразить в следующем виде

$B_{2}(\tau )=-2\pi \sigma ^{3}\sum _{n=0}^{\infty }{\frac {\tau ^{-n}}{n!(n\gamma -3)}}=-{\frac {2\pi \sigma ^{3}}{\gamma }}\left(-{\frac {1}{\tau }}\right)^{3/\gamma }\Gamma \left(-{\frac {3}{\gamma }},0,-{\frac {1}{\tau }}\right)$

Связь параметров уравнения Ван-дер-Ваальса с параметрами потенциала

Параметры уравнения Ван-дер-Ваальса можно связать с параметрами потенциала Сазерленда следующим образом:

$b={\frac {2}{3}}\pi \sigma ^{3}$

$a=b{\frac {3\varepsilon }{\gamma -3}}={\frac {2\pi \sigma ^{3}\varepsilon }{\gamma -3}}$

Вывод

В выражении для второго вириального коэффициента разложим экспоненту в ряд, ограничившись только первыми двумя слагаемыми $\exp \left[{\frac {1}{\tau x^{\gamma }}}\right]=1+{\frac {1}{\tau x^{\gamma }}}+...$

$B_{2}(\tau ){\bigg /}{\frac {2}{3}}\pi \sigma ^{3}=1-3\int _{1}^{\infty }x^{2}\left({\frac {1}{\tau x^{\gamma }}}\right){\text{d}}x=1-{\frac {3}{\tau (\gamma -3)}}=1-{\frac {3\varepsilon }{kT(\gamma -3)}}$

Обратим внимание, что получившийся интеграл сходится только при $\gamma >3$

Учитывая, что для уравнения Ван-дер-Ваальса

$B_{2}(T)=b-{\frac {a}{kT}}$

Получим выражения для параметров уравнения:

$b={\frac {2}{3}}\pi \sigma ^{3}$

$a=b{\frac {3\varepsilon }{\gamma -3}}={\frac {2\pi \sigma ^{3}\varepsilon }{\gamma -3}}$

Случай $\gamma =6$

При $\gamma =6$ второй вириальный коэффициент возможно выразить как

$B_{2}(\tau )={\frac {2}{3}}\pi \sigma ^{3}\left(e^{1/\tau }-{\sqrt {\frac {\pi }{\tau }}}{\text{Erfi}}{\frac {1}{\sqrt {\tau }}}\right)$

где ${\text{Erfi}}(z)$ — комплексная функция ошибок.

Температура Бойля и температура инверсии могу быть найдены из своих определений:

${\begin{array}{ll}B_{2}(T)=0&\Rightarrow T_{B}\approx 1.1709\varepsilon /k\\{\dfrac {{\text{d}}B_{2}(T)}{{\text{d}}T}}-{\dfrac {B_{2}(T)}{T}}=0&\Rightarrow T_{i}\approx 2.215\varepsilon /k\end{array}}$

Третий вириальный коэффициент

Третий вириальный коэффициент данного потенциала может быть получен в виде разложения по степеням $\tau$:

$B_{3}(\tau )=\sum _{n=0}^{\infty }{\frac {c_{n}}{\tau ^{n}}}$

где $c_{n}$ — коэффициенты, первые 11 из которых приведены в таблице.

Примечания

Комментарии

Источники

Литература

• Каплан И. Г. Введение в теорию межмолекулярных взаимодействий.. — М.: Наука. Главная редакция физико-математической литературы, 1982. — С. 312.
• M. P. Allen, D. J. Tildesley. Computer Simulation of Liquids. — Oxford University Press, 1990. — ISBN 0198556454. — ISBN 9780198556459.
• Цянь Сюэ-Сень. Физическая механика. — М.: Мир, 1965. — 544 с.
• D. Levi and M. de Llano. Closed form of second virial coefficient for Sutherland potential // Journal of Chemical Physics. — 1975. — Т. 63. — С. 4561—4562.
• Jianxiang Tian and Yuanxing Gui. Liquid-gas phase transition to first order of an argon-like fluid modeled by the hard-core similar Sutherland potential // International Journal of Modern Physics B. — 2004. — Т. 18. — С. 2057—2069.
• A. Díez, J. Largo and J. R. Solana. Structure and thermodynamic properties of Sutherland fluids from computer simulation and the Tang–Lu integral equation theory // Fluid Phase Equilibria. — 2007. — № 253. — С. 67—73.
• Jianguo Mi, Yiping Tang, and Chongli Zhong. Theoretical study of Sutherland fluids with long-range, short-range, and highly short-range potential parameters // Journal of Chemical Physics. — 2008. — Т. 128. — С. 054503.
• Roman Melnyk, Pedro Orea, Ivo Nezbeda, and Andrij Trokhymchuk. Liquid/vapor coexistence and surface tension of the Sutherland fluid with a variable range of interaction: Computer simulation and perturbation theory studies // Journal of Chemical Physics. — 2010. — № 132. — С. 134504.
• F. Paragand, F. Feyzi and B. Behzadi. Application of the SAFT-VR equation of state to vapor–liquid equilibrium calculations for pure components and binary mixtures using the Sutherland potential // Fluid Phase Equilibria. — 2010. — Т. 290. — С. 181—194.

См. также

• Межмолекулярное взаимодействие
• Потенциал Штокмайера
• Потенциал Букиннгема
• Потенциал Леннарда-Джонса

Ссылки

• Sutherland potential on SklogWiki.