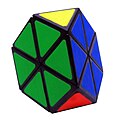
Молдавская пирамидка
| Пирамидка Мефферта Молдавская пирамидка Японский тетраэдр Тетраэдр Рубика | |
|---|---|
| Pyraminx | |
 | |
| Основная информация | |
| Изобретатель | Уве Мефферт |
| Год выпуска | 1981 |
| Кол-во возможных комбинаций | 75 582 720 |
| Число Бога | 11 ходов |
| Форма | тетраэдр |
Пирамидка Мефферта, ныне чаще называемая "Пираминкс" (англ. Pyraminx), «Молдавская пирамидка» или «Японский тетраэдр» — головоломка в форме правильного тетраэдра, подобная кубику Рубика. Каждая грань тетраэдра поделена на 9 правильных треугольников. Задача состоит в том, чтобы перевести пирамидку в конфигурацию с одноцветными гранями.
Иногда за схожесть с кубическим аналогом называют также «Тетраэдр Рубика», хотя Эрнё Рубик не имеет никакого отношения к созданию этой головоломки.
История
Головоломка была изобретена немцем Уве Меффертом, по словам автора, в 1972 году (якобы до изобретения кубика Рубика, запатентованного в 1975 году). Серийное производство началось в 1981 году японской корпорацией Tomy Toys (на тот момент — третья в мире по величине компания по выпуску игрушек). В том же году был зарегистрирован первый патент (EP0042695 от 30 декабря 1981 года (дата подачи 27 марта).
В СССР главный технолог Кишинёвского тракторного завода Александр Александрович Ордынец изобрёл эту головоломку и сделал заявку на изобретение на 40 дней раньше Мефферта (патент SU980739 от 15 декабря 1982 года с датой подачи 18 февраля 81-го. Его название головоломки - "Молдавская пирамидка".
Конструкция


Головоломка состоит из 14 подвижных элементов: 4 осевых (каждый из которых имеет треугольники, обращенные на 3 смежные грани), 6 рёберных и 4 тривиальных угловых. Осевые элементы имеют форму октаэдров, а рёберные и угловые — тетраэдров. При вращении частей пирамидки относительно рассекающих её плоскостей фрагменты перемещаются. Вращение происходит вокруг осей, направленных из центра к вершинам головоломки.
Конструктивно головоломка представляет собой 4-лучевую объёмную крестовину, на осях которой размещаются осевые и тривиальные элементы, а в специальным образом сформированные пазы помещены рёберные элементы, снабжённые выступами, позволяющими фрагментам свободно перемещаться при вращении головоломки, при этом не вываливаясь из неё.
Сборка
Сборка пирамидки проще сборки кубика Рубика. Взаимное расположение цветных граней осевых и тривиальных элементов задано конструкцией, и они легко выставляются в правильные положения (трилистник, аналог «креста» у кубика Рубика, только конструктивно он формируется одновременно для всех граней), после чего остаётся упорядочить 6 рёберных элементов.
Модификации
Пирамидка Дуэль

Пирамидка Дуэль (англ. Pyraminx Duo, первоначальное название ― Rob's Pyraminx) ― головоломка, созданная Оскаром ван Девентером на основе идеи Роба Стегманна. Состоит из 8 подвижных элементов: 4 угловых и 4 центральных. При вращении угловой части автоматически передвигаются и все центры.
Полное количество перестановок пирамидки равно .
Это число чрезвычайно мало по сравнению с другими головоломками, такими как карманный кубик, кубик Рубика и др. Из любого положения пирамидку можно собрать за четыре хода.
-
Собранная пирамидка
-
Пирамидка в движении
Пирамидка Кристалл

Пирамидка Кристалл (англ. Pyraminx Crystal) ― головоломка, вышедшая в серийное производство в 2008 году. Состоит из 50 подвижных элементов ― 20 углов и 30 рёбер. Имеет много общего как с пирамидкой Мефферта, так и с мегаминксом.
Число возможных перестановок головоломки равно ―
примерно 1,68 унвигинтиллиона.
Прочие
-
Мастер-пирамидка 4×4×4
-
Вариант, пирамидка Хелперн-Мейера
-
Пирамидка с элементами разной формы
-
Джинг-пирамидка
-
Тетраминкс



Существует головоломка под названием «Тетраминкс» (англ. Tetraminx) в форме усечённого тетраэдра, которая отличается от пирамидки Мефферта отсутствием тривиальных вершин.
Визуально похожая пирамидка меньшего размера — 2×2×2. Несмотря на внешнюю схожесть, она имеет принципиально другой механизм (аналогичный кубу 2×2×2). По этой причине в результате вращений форма головоломки меняется, задача сборки состоит не только в упорядочении цветов, но и в восстановлении тетраэдра[1].
Существует и просто пирамидка 2×2×2, где вращаются только тривиальные вершины.
В 2013 году Тони Фишер сделал из скьюба гигантскую пирамидку и гигантский тетраминкс, каждый треугольник имел длину 13 сантиметров. В 2017 году он сделал гигантский мастер пираминкс. Каждый треугольник также был 13 сантиметров ребром.
Если следовать логике, что разрезы должны проходить по линиям, являющимися кратчайшими прямыми, которые соединяют точки на равных отрезках на ребрах, то пираминкс — это 3х3х3 тетраэдр. По меньшей мере четыре раза разными инженерами (в том числе в СССР[2]) предпринимались попытки создать Master Pyraminx, пирамидку с 4 слоями[3][4][5][6], и с 2011 года началось их массовое производство, правда, детали были непропорциональными, а форма была скругленной. В 2017 году китайская фирма Shengshou (сейчас: Sengso) выпустила в массовое производство мастер мираминкс с нескруглёнными гранями и где все детали — одинаковые (равные) правильные треугольники. Позже этот мастер пираминкс появился от других производителей.
Позднее Тимур Эвбатыров (Башкирия) изобрёл Professor Pyraminx с 5 слоями[7][8], с 2011 года выпускался Меффертом вместе с мастер пираминксом, но позже был везде распродан и более не выпускался. В конце 2022 года компания Yuxin выпустила свой профессор пираминкс. В отличие от мастер пираминкса, сделать профессор и далее с одинаковыми деталями в виде равных правильных треугольников не выйдет, так как центральные ребра не смогли бы ни за что зацепиться и висели бы в воздухе. Но если использовать криволинейные/гиперболические разрезы, то можно сделать профессор пираминкс и далее с нескругленными сторонами.
Calvin puzzles в 2018 году начал выпускать Royal pyraminx, он же Королевская пирамидка, аналог с 6 слоями.
Существует и семислойная версия (Emperor pyraminx), но она существует лишь как прототип в единичном экземпляре, сделанном на 3d принтере Shapeways.
Jings pyraminx — добавляем в пирамидку невидимые центры.
Пирамидки 2х2х2, 4х4х4, 5х5х5 и 6х6х6, которые отличаются от младшей, мастер, профессор и королевской пирамидок. У них детали полностью совпадают с большими кубами. Это аналоги Jings pyraminx с 2, 4, 5 и 6 слоями соответственно.
Пирамидка Роба — прячем у пирамидки Джингса все ребра.
Скьюб — кубическая трансформация Jings pyraminx. У него есть 4х4х4 версия (F-скьюб), 5х5х5 (мастер скьюб) и 7х7х7 (элитный скьюб). Тони Фишер сделал 6х6х6 версию(у нее нет официального названия, но скорее всего, она называется мастер F-скьюб или Six-skewb/Six-cube), но в форме ромбододекаэдра. Также можно сделать 2х2х2, у которого просто бы вращались 4 тривиальных уголка, но любые 4х4х4 варианты можно использовать в роли 2х2х2, если вращать только пополам.
Предыдущие варианты можно проделать и с кубами 3х3х3 и 4х4х4. Получаются ромбододекаэдрические аналоги скьюбов. 4х4х4 ромбододекаэдр можно использовать в качестве 2х2х2, если не делать движения крайними слоями.
В линейке скьюбов-триаконтаэдров существует вариант из мегаминкса. Такой головоломки нет в продаже, но ее можно сделать вручную или при помощи трехмерной печати.
Если говорить про аналоги скьюбов в форме тетраэдра, октаэдра, икосаэдра и додекаэдра, то октаэдрическим подобием является Skewb diamond, а икосаэдрическим — икосамат(головоломка, двойственная пентультимейту). Для тетраэдрических и додекаэдрических скьюбов существует только длинная шкала, в которой додекаэдр пентультимейт — это 2х2х2, а мастер пентультимейт — 3х3х3 (в то время как для скьюбов и ромбододекаэдрических скьюбов была и длинная шкала, где скьюб — 2х2х2, а мастер — 3х3х3 и профессор — 4х4х4, и короткая, где мастер и профессор скьюбы были 5х5х5 и 7х7х7 аналогами соответственно скьюба, который считался как 3х3х3, а четным скьюбом (4х4х4) являлся F-скьюб). Аналоги скьюба в форме тетраэдра — это серия пираморфиксов, но где грани можно вращать только на 180 градусов. Обычный пираморфикс — 2х2х2 скьюб-тетраэдр, мастер пираморфикс — 3х3х3 и так далее. В данный момент максимальный тетраэдр в серийной продаже — это 10х10х10, который производит фирма SengSo. Если им играть, поворачивая стороны только на 180 градусов и никогда на 90, то это будет 10х10х10 скьюб-тетраэдр.
Если обычную пирамидку при помощи материалов превратить в куб, то выйдет кубоминкс (сделал Тони Фишер), причем он возможен как с прямыми, так и криволинейными (англ: curvy) разрезами. Последний называют «кубик плюща» (англ: Ivy cube). 5х5х5 версия по короткой шкале — рекс куб. 4х4х4 существует в форме ромбододекаэдра и называется Devil eyes (рус: Глаза дьявола). Евгений Григорьев (Чебоксары) сделал на 3д принтере кубические трансформации мастер и профессор пираминксов, которым дал названия Бинокулярный и Тринокулярный скьюб, однако, из-за криволинейных разрезов такое не получится проделать вручную с массово произведенными мастер и профессор пираминксами, если захочется сохранить доступность вращения всех слоев.
Как и крейзи кубы, есть серия пирамидок с фиксированными и подвижными кругами. Так как всего 4 стороны, чтобы получить все 8 планет, усложнили и добавили цельные стороны, на деталях которых нет кругов. Если хотя бы одна из таких деталек встанет этой частью на фиксированную сторону, то из-за прервавшегося круга он полностью заблокирует сторону и эту грань повернуть не выйдет.
Шестерёнчатая пирамидка или Gear pyraminx. По аналогии с шестеренчатым кубиком Рубика с пирамидкой проделали то же самое. Тимур Эвбатыров проделал то же самое с мастер пираминксом.
Вулкан — пазл с интересной геометрией. Его можно назвать cross pyraminx (то есть на каждую грань налеплена полностью функциональная грань) и тетраэдрической трансформацией F-скьюба (4×4×4 скьюба) одновременно. Мини версия — Junior volcano или диноморфикс.
По аналогии с кубоидами, делали аналоги на пирамидку. Получались в форме пентаэдров.
Крейзи пентаэдры, просто трехслойный пентаэдр без кругов и пятислойный пентаэдр.
Пиракоптер — аналог кубик «Вертолёт», но тетраэдрический. Геометрия интересна тем, что это тот же кубик Рубика 3×3×3, и он не блокируется в отличие от вертолёта кубического. С виду выглядит точь-в-точь, как пирамидка, но вращается не за счёт вершин, а за счёт рёбер.
Клевер пираминкс. Но у него нет такой асимметрии, как с ромбододекаэдром, поэтому это обычный 3х3х3, у которого детали не джамблятся (не происходит такого, что повороты блокируются при потере формы).
Ghost версия пирамидки и Jings pyraminx.
Зеркальная версия пирамидки.
Октаминкс — усекаем четыре вершины пираминкса и получаем октаэдр. 5х5х5 версия по короткой шкале — Face turning octahedron (сокращенно FTO). Это двойственная рекс кубу головоломка. Тони Фишер делал 4х4х4 версию по короткой шкале из головоломки Вулкан (чтобы сделать, надо урезать вершины и найти способ значительно укоротить винты. Деталей, которые были в вершинах, больше нет) и назвал ее Октригн (октаэдр+Тригн, так еще называют Вулкан, так как в нем форма тетраэдра и 4 объемные вершины в углах, от корней -тригн-, -тригоно-). При срезании 4 невидимые детали автоматически появляются и задаются. Самоцвет 5 (Gem 5) по своей сути тоже является 4х4х4 версией октаминкса или Скьюб Хекса, но у него форма не октаэдра, а усеченного октаэдра, и нет дополнительных лицевых слоев, как в головоломках Вулкан и Кросс куб, а так является одной и той же вариацией головоломки, просто в другом выполнении. Невозможно сделать четные октаэдры так, чтобы была и нескругленная форма, и прямолинейные разрезы, и без добавочных слоев. Иначе плоскости будут врезаться друг в друга, если не сделать вместо октаэдра усеченный октаэдр. На самом деле, в четных головоломках часто нет деталей по центру. И Октригн можно сделать, выбрав форму усеченного тетраэдра с добавочными слоями. Таким образом, в этом случае надо просто вынуть из Вулкана 12 тривиальных вершин(но которые могут размешиваться) и не надо будет дополнительно укорачивать винты. Мы получим прямолинейную нескругленную версию 4х4х4 октаминкса, у которого вдобавок не будет фиксированных центров, но он будет не в форме октаэдра, а усеченного тетраэдра, что одно и то же, потому что, сделав 4 стороны октаэдра выше, мы получим усеченный тетраэдр.
Скьюб-алмаз — двойственная скьюбу головоломка. Если следовать логике, что рисунок грани должен быть образован прямыми, проведенными из точек, которые делят ребра на 2,3,4… части, то в линейке есть Face turning октаэдр и мастер FTO. Если же брать короткую шкалу, то следующие в серии головоломки будут уже либо в форме усеченного тетраэдра, либо в форме усеченного октаэдра, либо иметь кросс-стороны (которые либо вращаются напрямую, либо косвенно, либо только имеют вид и не вращаются никак), либо искривленные разрезы. Можно сказать, что добавочные слои (кросс-стороны) или форма усеченного октаэдра/тетраэдра предотвращают криволинейные разрезы или кривизну, так как эти стороны будут нарощены выше, в этом пространстве также может быть механизм.
Октаэдр FTO, но с добавленными центральными деталями, и другими пропорциями деталей. Рисунок на гранях как на мастер FTO с объединенными тройками ребер. У него есть еще версии крейзи, правда, не 8 планет, а 5:Юпитер (1 фиксированный круг), Меркурий (1 нефиксированный, 3 фиксированных), Марс(2 подвижных,2 фиксированных), Сатурн (на 4 стороных фиксированные круги) и Венера(на всех 8 сторонах фиксированные круги).
Окончательный скьюб (Skewb Ultimate) — трансформ скьюба в додекаэдр. Другое название — Skewb ball, из-за сходства додекаэдра с шаром, к которому «стремятся» многие многогранники. У него есть версия стандартного размера и мини-брелок версия.
Скьюб Хекс (Skewb Hex) — тот же Skewb Diamond, у которого по аналогии с усеченным октаэдром усекли вершины. Следующие в линейке — Gem 5 (4х4х4) и Gem 4(двойственный пазл гибрида дино куба и скьюба. Опять же, чтобы не пересеклись плоскости, выбрана форма усеченного октаэдра вместо обычного октаэдра). Из кубика Рубика 4х4х4 можно получить аналог Gem 5 в форме ромбоусеченного кубооктаэдра, а из 6х6х6 можно получить следующий по счету Gem после 4, у которого больше слоев и глубокий поворот на 3 части, ромбоусеченной кубооктаэдрической формы.
Коршун (Skewb Kite) — ромбододекаэдр, сделанный из скьюба. Тони Фишер сделал из кубика Рубика 3х3х3 дельтоидальный икоситетраэдр. Так как большинство многогранников стремятся к шару, то достаточно просто взять мячик 3х3х3 и переклеить нужным образом наклейки. Следующие в линейке головоломки уже начинают иметь стороны, все меньше и меньше похожие на дельтоиды и все больше и больше похожие на квадраты, а сама фигура больше стремится к кубу и меньше напоминает дельтоидальный икоситетраэдр. Последняя головоломка здесь — это кубик 6х6х6, у которого на каждой стороне 3х3 квадраты разных цветов, всего 24 разных цвета, но это уже не дельтоидальный икоситетраэдр, а тот же куб, у которого каждая из 6 квадратных сторон поделена на 4 равных квадрата. Это «пропорциональная» версия. Получить дельтоидальный икоситетраэдр можно либо усечением, либо наращиванием. В первом случае получаются кривые разрезы, во втором — непропорциональные детали.
Пасхальное яйцо — что-то среднее между зеркальным фишер скьюбом, цилиндром и овалом.
Золотой куб Тони Фишера — ghost версия скьюба. Все детали разной формы и величины. Скьюб изначально смещен на один щелчок. Существуют прототипы следующего в линейке- Платинового куба (по аналогии с Золотым кубом из мастер скьюба). Есть один самодельный аналог для F-скьюба, но автор предпочел его сделать как скьюб-ромбододекаэдр из 4х4х4 и назвал его Бриллиантовый ромбододекаэдр.
Модификации скьюба в различные формы/фигуры.
Сиамские пирамидки. Или сиаминкс.
Комбинаторика
Каждый из 4 осевых и 4 вершинных элементов может быть ориентирован тремя способами независимо от состояния других элементов. Шесть рёберных элементов могут быть ориентированы 25 способами и расположены 6!/2 способами. Таким образом, число конфигураций равно
В головоломке «Тетраминкс» тривиальные вершины отсутствуют, поэтому число конфигураций меньше в 81 раз и равно 933120[9].
Для пирамидки 4×4×4 число конфигураций 217225462874112000 с учётом тривиальных вершин[10] и 2681795837952000 без их учёта [11] соответственно.
В общем случае для пирамидки с произвольным числом слоёв число конфигураций с учётом тривиальных вершин определяется последовательностью A309110[10], а без учёта - последовательностью A309109[11].
Оптимальное решение
Известно, что число Бога головоломки (минимально необходимое число поворотов для сборки пирамидки при оптимальном методе сборки) равно 11. Имеется всего 933 120 возможных перестановок цветов на гранях (исключая расположение тривиальных угловых элементов), что позволяет определить оптимальное решение для каждой конфигурации методом полного перебора[9][12].
Следующая таблица показывает число конфигураций, которые могут быть решены в n ходов, но не могут быть решены меньше, чем в n ходов.
| n | число конфигураций |
|---|---|
| 0 | 1 |
| 1 | 8 |
| 2 | 48 |
| 3 | 288 |
| 4 | 1728 |
| 5 | 9896 |
| 6 | 51 808 |
| 7 | 220 111 |
| 8 | 480 467 |
| 9 | 166 276 |
| 10 | 2457 |
| 11 | 32 |
См. также
Примечания
- ↑ Пирамидка 2×2. Дата обращения: 15 июня 2010. Архивировано 10 августа 2011 года.
- ↑ Советские головоломки от конструктора Ордынца или кто первый изобрёл Пирамидку? Дата обращения: 23 сентября 2018. Архивировано 23 сентября 2018 года.
- ↑ Le Master Pyraminx / Univers Cubique / Créations — Les Forums du Refuge d’Aerie’s Guard. Дата обращения: 10 апреля 2011. Архивировано из оригинала 29 мая 2014 года.
- ↑ Master Pyraminx by shim on Shapeways (недоступная ссылка)
- ↑ TwistyPuzzles.com Forum • View topic — The Master Pyraminx — now with video. Дата обращения: 10 апреля 2011. Архивировано 29 мая 2014 года.
- ↑ YouTube — Master Pyraminx
- ↑ TwistyPuzzles.com Forum • View topic — Professor Pyraminx Shipping. Дата обращения: 10 апреля 2011. Архивировано 29 мая 2014 года.
- ↑ YouTube — Professor Pyraminx
- ↑ 1 2 Jaap Scherphuis. Pyraminx (англ.). Jaap's Puzzle Page. Дата обращения: 29 июля 2013. Архивировано 29 августа 2013 года.
- ↑ 1 2 последовательность A309110 в OEIS. Дата обращения: 9 октября 2021. Архивировано 9 октября 2021 года.
- ↑ 1 2 Последовательность A309109 в OEIS. Архивировано 9 октября 2021 года.
- ↑ последовательность A079744 в OEIS
Литература
- И. Константинов. Вокруг кубика // Наука и Жизнь. — 1982. — № 7. — С. 100 — 102.
- В. Н. Николаев. Венгерский кубик и молдавская пирамидка (по страницам книг и журналов). Дата обращения: 29 июля 2013.
Ссылки
- Jaap Scherphuis. Pyraminx (англ.). Jaap's Puzzle Page. Дата обращения: 29 июля 2013. Архивировано 29 августа 2013 года.
- Уве Мефферт, создатель головоломки Архивная копия от 14 июля 2010 на Wayback Machine