Гиппарх

Материал из Википедии — свободной энциклопедии
Это старая версия этой страницы, сохранённая Girin (обсуждение | вклад) в 12:16, 2 мая 2010 (→Ссылки). Она может серьёзно отличаться от текущей версии.
Перейти к навигации Перейти к поиску
Отпатрулированная версия этой страницы, проверенная 30 мая 2010, была основана на этой версии.
Экваториальное кольцо — инструмент, использовавшийся Гиппархом для наблюдения равноденствий. Его тень падает на сам прибор только тогда, когда Солнце находится на экваторе (то есть в точках равноденствий). Таким образом, с помощью этого инструмента можно с довольно высокой точностью определять моменты равноденствий.
В Википедии есть статьи о других людях с именем Гиппарх.

Гиппа́рх Нике́йский (ок. 190 до н. э. — ок. 120 до н. э.) (др.-греч. Ἳππαρχος) — древнегреческий астроном, географ и математик II века до н. э., часто называемый величайшим астрономом античности. Главной заслугой Гиппарха считается то, что он привнёс в греческие геометрические модели движения небесных тел предсказательную точность астрономии Древнего Вавилона.

Биография

Гиппарх родился в Никее (в настоящее время Изник, Турция). Большую часть жизни проработал на острове Родос, где он, вероятно, и скончался. Его первое и последнее астрономические наблюдения датируются, соответственно, 162 и 127 гг. до н. э. Предполагается, что он был в контакте с астрономами Александрии и Вавилона, но неизвестно, посещал ли он эти научные центры лично. Основным источником информации о его трудах является «Альмагест» Птолемея; последний оставил следующую характеристику Гиппарха: «муж трудолюбец и поклонник истины». Из собственных сочинений Гиппарха до нас дошло только одно, критический комментарий к популярной астрономической поэме Арата.

Прецессия

Наиболее важным достижением Гиппарха считается открытие предварения равноденствий, или астрономической прецессии, заключающееся в том, что точки равноденствий постепенно перемещаются среди звёзд, благодаря чему каждый год равноденствия наступают раньше, чем в предшествующие годы. По Птолемею, Гиппарх сделал это открытие, сопоставляя координаты Спики, измеренные александрийским астрономом Тимохарисом с определёнными им самим. Более подробное исследование позволило Гиппарху отвергнуть предположение, что это изменение координат вызывается собственными движениями звёзд, так как менялись только долготы звёзд (их угловые расстояния от точки весеннего равноденствия, отсчитываемые вдоль эклиптики), но не их широты (угловые расстояния от эклиптики). По Гиппарху, скорость прецессии составляет 1˚ в столетие (на самом деле, 1˚ за 72 года).

По мнению американского историка науки Ноула Свердлоу (Swerdlow)[1], измерения звёздных координат, бывших в распоряжении Гиппарха, являются недостаточно точными, чтобы судить о скорости прецессии. Свердлоу предполагает, что Гиппарх измерил скорость прецессии на основании разности между тропическим и сидерическим (звёздным) годами. В последнее время появились основания полагать[2], что разность между этими двумя видами года была известна ещё Аристарху Самосскому полтора столетия раньше Гиппарха. Если это так, то заслуга Гиппарха заключается не столько в открытии прецессии, сколько в подробном исследовании этого феномена на основе данных о координатах звёзд.

Звёздный каталог

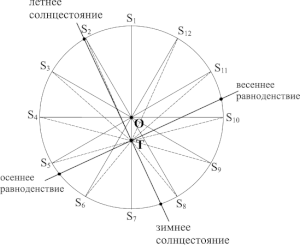
Гиппарх составил первый в Европе звёздный каталог, включивший точные значения координат около тысячи звёзд (работу по определению звёздных координат начали ещё в первой половине III века до н. э. Тимохарис и Аристилл в Александрии). Плиний Старший писал, что непосредственным поводом к составлению каталога явилась новая звезда в Змееносце, натолкнувшая Гиппарха на мысль, что «надлунный мир» также подвержен изменениям, как и мир земной: «Он определил места и яркость многих звёзд, чтобы можно было разобрать, не исчезают ли они, не появляются ли вновь, не движутся ли они, меняются ли в яркости. Он оставил потомкам небо в наследство, если найдётся тот, кто примет это наследство». Отсюда видно, что сам Гиппарх, по меньшей мере, допускал возможность собственных движений звёзд. Имея в виду оставить позднейшим наблюдателям данные для наиболее лёгкого определения изменения положений звёзд, он записал несколько случаев, когда три или более звезды лежат примерно на одной линии (большом круге небесной сферы). Заметим, что наличие собственных движений несовместимо с представлением о звёздах как о телах, закреплённых на одной сфере; представление о неподвижности Земли требует, чтобы звёзды были жёстко закреплены на небесной сфере, поскольку в этом случае суточное вращение неба считается реальным, а не кажущимся, как в случае вращающейся Земли. Хотя большинство астрономов считают Гиппарха сторонником мнения о неподвижности Земли, можно допустить, что он, по крайней мере, не исключал возможность вращения Земли.

Другим новшеством Гиппарха при составлении каталога явилась система звёздных величин: звёзды первой величины самые яркие и шестой — самый слабые, видимые невооружённым взглядом. Эта система в усовершенствованном виде используется в настоящее время.

Сам по себе каталог Гиппарха до нас не дошёл. Многие астрономы (начиная с Тихо Браге) полагают, однако, что звёздный каталог, приведённый в «Альмагесте» Птолемея в действительности является переделанным каталогом Гиппарха, вопреки высказыванию Птолемея, что все звёзды его каталога наблюдались им самим. По этому вопросу ведётся очень напряжённая дискуссия, но в последнее время начинает преобладать мнение об авторстве Гиппарха. В частности, к такому выводу пришли в 2000 г. А. К. Дамбис и Ю. Н. Ефремов[3], определив эпоху составления каталога по данным о собственных движениях звёзд.

Некоторые исследователи[4] считают также, что звёздный глобус, являющийся деталью эллинистической скульптуры «Атлас Фарнезе» изготовлен на основе каталога Гиппарха. По этому вопросу также ведётся дискуссия[5] [6].

Календарные периоды

Гиппарх внёс существенный вклад в усовершенствование календаря. Он определил продолжительность тропического года 365+(1/4)-(1/300) дней (на 6 минут длиннее правильного значения во II в. до н. э.) Традиционно считается, что он получил это значение исходя из промежутка времени между летними солнцестояниями, наблюдёнными в 280 г. до н. э. Аристархом и/или его школой в Александрии и самим Гиппархом в 135 г. до н. э. на Родосе, но, по мнению, высказанному Тобиасом Майером в конце XVIII века и поддержанному Н. Свердлоу[7] и Д. Роулинзом (Rawlins)[8], Гиппарх получил это значение исходя из продолжительности метонова цикла (19 лет, или 235 синодических месяцев), или его модификации по Каллиппу (4 метоновых цикла минус 1 день) и продолжительности синодического месяца 29 дней 31'50"08'"20"", которое Гиппарх мог заимствовать у вавилонских астрономов (по Свердлоу) или у Аристарха (по Роулинзу).

Разность между тропическим и сидерическим годами определяется прецессией; по Галену, гиппархово значение сидерического года оставляет 365+(1/4)+(1/144) дней.

На основании своего определения длины тропического года, Гиппарх внёс очередное усовершенствование в лунно-солнечный календарный цикл: 1 цикл Гиппарха составляет 4 цикла Каллиппа (304 года) без одного дня, т.е. 111 035 дней, или 3760 синодических месяцев.

С Гиппархом может быть связано ещё одно определение длины тропического года, 365,24579 дней, или 365+(1/4)-(5/1188) дней. Это значение встречается в вавилонских глиняных таблицах. Как показал Деннис Роулинз[9], оно почти наверняка получено исходя из промежутка времени между летними солнцестояниями Гиппарха (упомянутым выше) и наблюдённого в 432 г. до н. э. Метоном и Евктемоном в Афинах. Эта оценка могла быть получена самим Гиппархом или, скорее, кем-то из его учеников и затем попасть на Восток, где была положена в основу одной из вавилонских теорий движения Солнца по небу (вопреки традиционному мнению, предполагающему поток информации из Вавилона в Грецию; в связи с этим отметим аргументированное мнение Роулинза, что значение длины синодического месяца 29 дней 31'50"08'"20"", также встречающееся в вавилонских таблицах, было впервые получено Аристархом Самосским[10]).

Птолемей сообщает также, что Гиппарх установил связь между различными видами месяца:

4267 синодических месяцев = 4573 аномалистическим месяцам = 4612 сидерическим месяцам = 126007 дней + 1 час = 345 лет - 7˚30'.

Кроме того, по Гиппарху, 5458 синодических месяцев соответствуют 5923 драконическим месяцам.

Орбиты Солнца и Луны

Эквивалентность эпицикла и эксцентра в солнечной теории Гиппарха. T — Земля (центр деферента), S — Солнце, P — центр эпицикла, O — центр эксцентра (результирующей орбиты Солнца). По Гиппарху, OT=1/24 TP. При движении Солнца отрезки SP и OT всегда параллельны.

Все теории движения небесных тел, созданные вавилонскими астрономами, рассматривали только их движения по небу, к тому же только в проекции на эклиптику (что было вполне достаточно, с точки зрения астрологии, для нужд которой эти теории создавались). Наоборот, астрономы Древней Греции стремились установить орбиты небесных тел в пространстве. Начиная с Аполлония Пергского, III век до н. э. (а по мнению выдающегося математика и историка науки Бартела ван дер Вардена[11], ещё с пифагорейцев в доплатонову эпоху), они строили орбиты на основе сочетания больших и малых кругов — деферентов и эпициклов. Именно на основе этого принципа Гиппарх создал первые дошедшие до нас теории движения Солнца и Луны.

Если бы Солнце (в геоцентрической системе) равномерно двигалось по окружности с центром в центре Земли, то угловая скорость его перемещения по небу была бы постоянной и астрономические времена года имели бы равную продолжительность. Однако ещё Евктемон и позднее Каллипп установили, что продолжительность сезонов не одинакова: по собственным измерениям Гиппарха, более точным, чем у его предшественников, интервал между весенним равноденствием и летним солнцестоянием составил 94,5 дней, между летним солнцестоянием и осенним равноденствием — 92,5 дней. Поэтому согласно теории Гиппарха дневное светило равномерно движется по эпициклу, центр которого в свою очередь равномерно вращается по деференту. Периоды обоих вращений одинаковы и равны одному году, их направления противоположны, в результате чего Солнце равномерно описывает в пространстве окружность (эксцентр), центр которой не совпадает с центром Земли. Ван дер Варден[12] считает, что аналогичные теории Солнца создавались ещё раньше, в частности, Каллиппом в IV веке до н. э.

Движение Солнца в теории Гиппарха (модель эксцентра). O — центр орбиты Солнца, T — Земля. Через равные промежутки времени Солнце последовательно проходит через точки S1, S2 и т.д. таким образом, что углы S1OS2, S2OS3 и т.д. равны. Однако ввиду эксцентрического положения Земли углы S1TS2, S2TS3 и т.д. оказываются разными, что приводит к неравномерности движения Солнца по эклиптике и неравенству времён года.

Из наблюдений требовалось определить эксцентриситет орбиты (то есть отношение расстояний между центрами Земли и эксцентра) и направление линии апсид (линии, проходящей через центры Земли и эксцентра). Зная продолжительность времён года, Гиппарх решил эту задачу: эксцентриситет орбиты Солнца составляет 1/24, апогей орбиты расположен на угловом расстоянии 64,5° от точки весеннего равноденствия. Теория Гиппарха описывает положение Солнца на небе с очень высокой точностью. Точность определения расстояния Солнца от Земли оказывалась существенно ниже (из-за того, что реальная орбита Земли — эллипс, а не окружность), но соответствующая вариация видимого радиуса Солнца не была доступна для измерения древним астрономам. По мнению Роулинза[13], Гиппарх создал несколько таких теорий, каждая последующая из которых была точнее предыдущей, причём до нас дошла (благодаря «Альмагесту») только одна из них, притом не самая последняя.

Поскольку, в отличие от Солнца, периоды наиболее быстрого или медленного движения Луны по небу каждый месяц приходятся на новое созвездие, для создания теории движения Луны Гиппарху пришлось предположить, что скорости движения Луны по деференту и эпициклу не совпадают. Для получения орбитальных параметров Гиппарх использовал красивый метод, основанный на использовании трёх лунных затмений, созданной ранее им же теории Солнца и данных более ранних древнегреческих астрономов. Гиппарх создал две теории с несколько различными параметрами. Ввиду сложности движения нашего естественного спутника, лунная теория Гиппарха оказалась не столь успешной, как его теория Солнца, но тем не менее позволила осуществлять предсказания затмений с точностью, недоступной более ранним астрономам, в том числе вавилонским.

Интересно, что по одной из гиппарховых лунных теорий отношение радиусов эпицикла и деферента составляет 327+2/3 к 3144, по второй — 247+1/2 к 3122+1/2. Отношения чисел однозначно определяются из наблюдений, но откуда взялись эти странные единицы? Вопрос оставался неясным до 1991 года, когда Роулинз обнаружил[14], что при определении радиуса деферента использовались тысячные доли расстояния от Земли до Солнца (астрономической единицы), принятого в древности после Аристарха. Далее, Роулинз утверждает, что астрономическая единица является естественной мерой расстояний для гелиоцентристов, в то время как геоцентристы использовали для этой цели радиус Земли. Действительно, гелиоцентрист Коперник использовал астрономическую единицу, геоцентрист Птолемей — радиус Земли. Отсюда Роулинз делает вывод, что сотрудниками Гиппарха, непосредственными вычислителями, были астрономы, являвшиеся сторонниками гелиоцентризма.

Птолемей сообщает, что Гиппарх не занимался разработкой аналогичных теорий движений планет, ограничившись критикой существовавших в его время теорий. Главный дефект, который выявил Гиппарх в этих теориях, заключался в том, что даваемые ими попятные движения планет всегда имели одни и те же продолжительность и длину.

Вычисление расстояний до Луны и Солнца и их размеров

Первым, кто попытался измерить эти величины, был Аристарх Самосский. По его оценкам, Луна примерно в 3 раза меньше Земли по диаметру, а Солнце в 6,5 раз больше; Солнце в 19 раз дальше от нас, чем Луна. В книге, посвящённой этому вопросу, Аристарх не приводит значение расстояния до Луны, но его можно реконструировать: получается 80 радиусов Земли. По мнению С. В. Житомирского[15], этим занимался также Архимед, получивший расстояние до Луны около 62 радиусов Земли.

Как сообщают Птолемей и математик Папп Александрийский, Гиппарх написал две книги «О размерах и расстояниях», посвящённые измерению расстояний до Луны и Солнца. Реконструкции попыток Гиппарха определить эти параметры предпринимали Ф. Хюлч (Hultsch), Н. Свердлоу [16], Г. Тумер [17], Д. Роулинз[18].

В первой книге Гиппарх использовал наблюдения солнечного затмения, которое в Геллеспонте наблюдалось в полной фазе, а в Александрии в фазе 4/5. Предполагая, что Солнце гораздо дальше от нас, чем Луна, то есть солнечный параллакс пренебрежимо мал, Гиппарх получил минимальное расстояние до Луны 71 и максимальное 83 радиусов Земли. Во второй книге Гиппарх использует метод определения расстояния до Луны, основанный на анализе лунных затмений (в принципе аналогичный использованному ранее Аристархом и предполагает, что суточный параллакс Солнца составляет 7' — максимальная величина, при которой он неразличим невооруженным взглядом. В результате получается, что минимальное расстояние до Луны составляет 67 1/3, максимальное 72 2/3 радиусов Земли; расстояние до Солнца, соответствующее суточному параллаксу 7', составляет 490 радиусов Земли.

По всей видимости, Гиппарх неоднократно возвращался к этой теме. Теон Смирнский и Халкидий утверждают, что он получил объем Солнца в 1880 раз превосходящим объем Земли, и объем Луны – в 27 раз меньшим объема Земли. Эти числа не совпадают с приводимыми Паппом Александрийским. Зная угловой радиус Луны (1/1300 полного круга по Гиппарху), отсюда можно получить и расстояние до Луны: примерно 69 радиусов Земли, довольно близкое ко второй оценке Гиппарха, согласно Паппу (а если округлить видимый радиус Луны до ближайшей минуты, т.е. принять его равным 17', то мы получим как раз 67 1/3). Наконец, по свидетельству Клеомеда, отношение объемов Солнца и Земли по Гиппарху равно 1050.

Механика

Гиппарх написал книгу «О телах, движущихся вниз под действием их тяжести», с основными идеями которой мы знакомы в пересказе Симпликия. Гиппарх не разделял концепцию естественных и насильственных движений Аристотеля, согласно которой "тяжёлым" земным телам свойственно движение вниз, к центру мира, а "лёгким" (например, огню) — вверх, от центра. Согласно Симпликию, «Гиппарх пишет, что если бросить кусок земли прямо вверх, причиной движения вверх будет бросившая сила, пока она превосходит тяжесть брошенного тела; при этом, чем больше бросившая сила, тем быстрее предмет движется вверх. Затем, по мере уменьшения силы, движение вверх будет происходить со всё убывающей скоростью, пока, наконец, тело не начнёт двигаться вниз под действием своего собственного влечения — хотя в какой-то мере бросившая сила ещё будет в нём присутствовать; по мере того, как она иссякает, тело будет двигаться вниз всё быстрее и быстрее, достигнув своей максимальной скорости, когда эта сила окончательно исчезнет». По сути дела, здесь перед нами первое высказывание концепции импетуса, широко распространённой среди средневековых учёных (например, у Иоанна Филопона, Жана Буридана). Симпликий продолжает: Гиппарх «приписывает ту же причину и телам, падающим с высоты. А именно в этих телах также имеется сила, которая удерживала их на высоте, и действием этой силы объясняется более медленное движение тела в начале его падения». Эта концепция Гиппарха напоминает современное понятие потенциальной энергии. К сожалению, эти идеи Гиппарха не получили развития в античности.

Математик и историк науки Лучио Руссо (Russo)[19] полагает, что Гиппарх был знаком с понятием инерции и дал качественное описания действия тяготения. Таким образом он интерпретирует некоторые пассажи в сочинении Плутарха «О лике, видимом на диске Луны». По мнению Руссо, Гиппарх в действительности был гелиоцентристом, но его соответствующие труды не дошли до Птолемея.

Другие работы

Математика. При разработке теорий Луны и Солнца Гиппарх использовал античный вариант тригонометрии. Возможно, он первым составил таблицу хорд, аналог современных таблиц тригонометрических функций.

География. О вкладе Гиппарха в географию сообщает Страбон. Гиппарх определил географические координаты ряда пунктов. Он написал сочинение «Против Эратосфена», где резко и отчасти несправедливо критикует последнего за использование ненадёжных источников (свидетельств моряков, купцов) при определении местоположения населённых пунктов, считая, что для определения широт и долгот (ему также приписывают введение этих понятий) можно использовать только точные астрономические данные. Удовлетворить этому строгому требованию человечество оказалось не в состоянии более полутора тысячелетий, да Гиппарх и сам был вынужден прибегать к свидетельствам того типа, которые он критиковал.

Астрология. Возможно, великий астроном не был чужд и астрологии, проникшей в эллинистический мир из Вавилона. Как пишет Плиний Старший, «этот Гиппарх, который не может не заслужить достаточной похвалы... более чем кто-либо доказал родство человека со звёздами и то, что наши души являются частью неба». Гиппарх оказался одним из первых астрономов древности, занявшихся астрологией, и иногда упоминался в древних списках знаменитых астрологов.

В честь Гиппарха назван лунный кратер, астероид и орбитальный телескоп Европейского космического агентства, предназначенный для астрометрических измерений.

Примечания

  1. ↑ N. M. Swerdlow, Hipparchus’s determination of the length of the tropical year and the rate of precession, Arch. Hist. Exact Sci., V. 21(4), pp. 291—309, 1979/80. Online
  2. ↑ D. Rawlins, DIO: The International Journal of Scientific History, V. 9.1, pp. 31-38, 1999. Сайт журнала
  3. ↑ А. К. Дамбис и Ю. Н. Ефремов, Датировка звёздного каталога Птолемея по собственным движениям, Историко-астрономические исследования, вып. XXVI, сс. 7–25. — M.: Наука, 2001.Online см. также на Астронете
  4. ↑ B. Schaefer, Discovery of the lost star catalog of Hipparcjus on the Farnese Atlas
  5. ↑ D. Duke, The Farnese Globe
  6. ↑ D. Rawlins, Farnese Atlas Celestial Globe: Proposed Astronomical Origins
  7. ↑ N. M. Swerdlow, Op. cit., 1979/80.
  8. ↑ D. Rawlins, Op. cit., 1999.
  9. ↑ D. Rawlins, DIO: The International Journal of Scientific History, V. 1.1, pp. 49-66, 1991. Сайт журнала
  10. ↑ D. Rawlins, DIO: The International Journal of Scientific History, V. 11.1, pp. 5-9, 2002. Сайт журнала
  11. ↑ B. L. van der Waerden, The Earliest Form of the Epicycle Theory, Journal of the History of Astronomy, Vol. 5, p.175, 1974. Online
  12. ↑ B. L. van der Waerden, The Motion of Venus, Mercury and the Sun in Early Greek Astronomy, Archive for History of Exact Sciences, Volume 26, Number 2, 99 - 113, 1982. Online
  13. ↑ D. Rawlins, Op. cit., 1991.
  14. ↑ D. Rawlins, DIO: The International Journal of Scientific History, V. 1.3, pp. 159-162, 1991. Сайт журнала
  15. ↑ С. В. Житомирский, «Античная астрономия и орфизм», М., Янус-К, 2001.
  16. ↑ N. M. Swerdlow, Hipparchus on the distance of the sun, Centaurus, V. 14, pp.287-305, 1969.
  17. ↑ G. J. Toomer, Hipparchus on the Distances of the Sun and Moon, Arch. Hist. Exact Sci. 14, pp.126-142, 1974. Online
  18. ↑ D. Rawlins, DIO: The International Journal of Scientific History, V. 1.3, pp.168-172, 1991. Сайт журнала
  19. ↑ L. Russo, The astronomy of Hipparchus and his time: A study based on pre-ptolemaic sources, Vistas in Astronomy, V. 38, Pt 2, pp. 207-248, 1994. Сайт журнала

Ссылки

Литература

  • Клавдий Птолемей. Альмагест, перевод с древнегреческого И. Н. Веселовского. — М.: Наука-Физматлит, 1998.
  • А. Паннекук, История астрономии. — М.: Наука, 1966.
  • А. Берри, Краткая история астрономии. — М.-Л., ОГИЗ, 1946.
  • Н. И. Идельсон, Этюды по истории небесной механики. — М.: Наука, 1975.
  • И. Д. Рожанский, История естествознания в эпоху эллинизма и Римской империи. — М.: Наука, 1988.
  • Шаль, Мишель. Исторический обзор происхождения и развития геометрических методов, § 18. М., 1883
  • A. Franklin, Principle of inertia in the Middle Ages, American Journal of Physics, June 1976, V. 44, Issue 6, pp. 529–545 (специальный раздел посвящен механике Гиппарха).
  • A. Jones, Hipparchus in "Encyclopedia of Astronomy and Astrophysics", Nature Publishing Group, 2001.
  • K. Pickering, The Instuments Used by Hipparchos, DIO: The International Journal of Scientific History, V. 12, no.4. Сайт журнала
  • L. Russo, The Forgotten Revolution: How Science Was Born in 300 BC and Why It Had To Be Reborn. — Berlin: Springer, 2004.
  • M. Wolff, Hipparchus and the Stoic Theory of Motion'. In: Jonathan Barnes & Mario Mignucci (Hgg.), Matter and Metaphysics, Napoli: Bibliopolis, 1989, 346-419.

Шаблон:Link FA

Источник — https://ru.wikipedia.org/ruwiki/w/index.php?title=Гиппарх&oldid=24243938