Двумерное пространство

Двуме́рное простра́нство (иногда говорят двухме́рное пространство) — геометрическая модель плоской проекции физического мира, в котором мы живём. Двумерным пространством считается n-мерное пространство, где n=2.

Примером двумерного пространства является плоскость. Точки данного пространства возможно задать всего двумя числами. Например, любую точку можно задать парой чисел: (x, y). Плоские объекты характеризуются не только длиной, но и шириной.

Геометрия двумерного пространства

Многогранники

Основная статья: Многоугольник

В двумерном пространстве существует бесконечно много правильных многогранников: правильные многоугольники. Примеры последних приведены ниже:

Гиперсфера

Основные статьи: Окружность и круг

Гиперсферой в двумерном пространстве является окружность, которую иногда называют 1-сфера, потому что её поверхность является одномерной. Площадь части плоскости, заключённой внутри гиперсферы (площадь круга) равна:

$A=\pi r^{2}$,

где $r$ — радиус окружности.

Системы координат в двумерном пространстве

Основная статья: Система координат

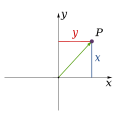
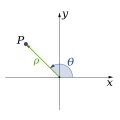
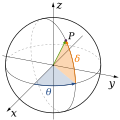
Наиболее распространённые координатные системы — прямоугольная (Декартова) система координат, полярная система координат и географическая координатная система.

• 
  Прямоугольная система координат
• 
  Полярная система координат
• 
  Географические координаты

См. также

• Двумерное нормальное распределение