Ориентированный граф

Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках (Оре) и просто рёбрами.
Основные понятия
Формально, орграф D=(V, E) есть множество E упорядоченных пар вершин .
Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.
Орграф, полученный из простого графа ориентацией ребер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.
Направленный полный граф называется турниром.
Связность
Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг, вида (вершины могут повторяться). Длина маршрута — количество дуг в нем.
Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.
Контур есть замкнутый путь.
Для полумаршрута снимается ограничение на направление дуг, аналогично определяются полупуть и полуконтур.
Орграф сильно связный, или просто сильный если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;
Максимальный сильный подграф называется сильной компонентой; односторонняя компонента и слабая компонента определяются аналогично.
Конденсацией орграфа D называют орграф D*, вершинами которого служат сильные компоненты D, а дуга в D* показывает наличие хотя бы одной дуги между вершинами, входящими в соответствующие компоненты.
Дополнительные определения
Направленный ациклический граф или гамак есть бесконтурный орграф.
Ориентированный граф, полученный из заданного сменой направления ребер на противоположное, называется обратным.
Изображение и свойства всех орграфов с тремя узлами
Легенда: С — слабый, ОС — односторонний, СС — сильный, Н — является направленным графом, Г — является гамаком (ациклический), Т — является турниром
| 0 дуг | 1 дуга | 2 дуги | 3 дуги | 4 дуги | 5 дуг | 6 дуг |
 пустой, Н, Г пустой, Н, Г |
 Н, Г Н, Г |
 |
 ОС ОС |
 CC CC |
 CC CC |
 полный, CC полный, CC
|
|---|---|---|---|---|---|---|
 ОС, Н, Г ОС, Н, Г |
 CC, Н, Т CC, Н, Т |
 CC CC |
||||
 C, Н, Г C, Н, Г |
 ОС, Н, Г, Т ОС, Н, Г, Т |
 ОС ОС |
||||
 C, Н, Г C, Н, Г |
 ОС ОС |
 ОС ОС |
Применение орграфов
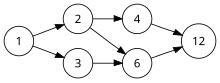
Орграфы широко применяются в программировании как способ описания систем со сложными связями. К примеру, одна из основных структур, используемых при разработке компиляторов и вообще для представления компьютерных программ — граф потоков данных.
Бинарные отношения
Бинарное отношение над конечным носителем может быть представлено в виде орграфа. Простым орграфом представимы антирефлексивные отношения, в общем случае требуется орграф с петлями. Если отношение симметрично, то его можно представить неориентированным графом, а если антисимметрично, то направленным графом.
Примечания
Литература
- Харари Ф. Теория графов. — М.: УРСС, 2003. — 300 с. — ISBN 5-354-00301-6.
- Оре, Ойстин. Теория графов. — М.: УРСС, 2008. — 352 с. — ISBN 978-5-397-00044-4.
- Альфред В. Ахо, Моника С. Лам, Рави Сети, Джеффри Д. Ульман. Компиляторы: принципы, технологии и инструменты, 2 издание = Compilers: Principles, Techniques, and Tools. — 2 изд. — М.: «Вильямс», 2008. — ISBN 978-5-8459-1349-4.
Это заготовка статьи по математике. Помогите Википедии, дополнив её. |

