Гипоциклоида


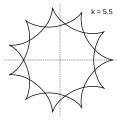
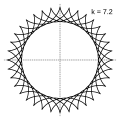
Гипоцикло́ида (от греческих слов ὑπό — под, внизу и κύκλος — круг, окружность) — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.
Уравнения
где , где — радиус неподвижной окружности, — радиус катящейся окружности.
|
Почему это так Пусть в начальный момент окружности касаются в точке А, лежащей на оси OX, где т.О - центр большой окружности. Координаты т.А при этом - (kr, 0), где R/r = k. Рассмотрим, как меняются координаты т.А, привязанной к катящейся окружности (т.А переходит в т.A'). Пусть маленькая окружность прокатилась так, что ее центр перешел из т.C в т.С' и повернулся относительно т.О на угол t. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между CA и C'A') равен t - kt = -(k-1)t. Во-вторых, координаты т.C' будут такими: ((k-1)r cos(t), (k-1)r sin(t)). Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты т.А':
|
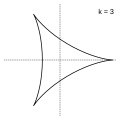
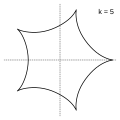
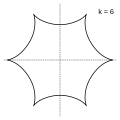
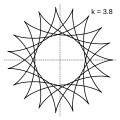
Модуль величины определяет форму гипоциклоиды. При гипоциклоида представляет собой диаметр неподвижной окружности, при является астроидой.