Формула конечных приращений

Приращение

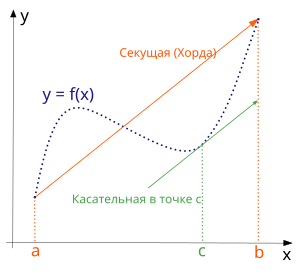
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция $f$ непрерывна на отрезке $[a;b]$ и дифференцируема в интервале $(a;b)$, то найдётся такая точка $c\in (a;b)$, что

${\frac {f(b)-f(a)}{b-a}}=f'(c)$.

Геометрически это можно переформулировать так: на отрезке $[a;b]$ найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Механическое истолкование: Пусть $f(t)$ — расстояние точки в момент $t$ от начального положения. Тогда $f(b)-f(a)$ есть путь, пройденный с момента $t=a$ до момента $t=b$, отношение ${\frac {f(b)-f(a)}{b-a}}$ — средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени $t\in (a,b)$, то в некоторый момент она будет равна своему среднему значению на этом участке.

Доказательство

Для функции одной переменной:

Введем функцию $F(x)=f(x)-{\frac {f(b)-f(a)}{b-a}}(x-a)$. Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны. Воспользовавшись упомянутой теоремой, получим, что существует точка $c$, в которой производная функции $F$ равна нулю:

$F'(c)=f'(c)-{\frac {f(b)-f(a)}{b-a}}=0\Leftrightarrow {\frac {f(b)-f(a)}{b-a}}=f'(c),$

что и требовалось доказать.

Конечные и бесконечно малые приращения

Название «конечные приращение» объясняется тем фактом, что, если в формуле $f(b)-f(a)=f'(c)(b-a)$, левую часть обозначить как $\Delta y$, а в правой части фактор $(b-a)$ обозначить через $\Delta x$, то мы получим формулу в представлении:

$\Delta y=f'(c)\Delta x$

что в свою очередь уже очень похоже на определение дифференциала:

$dy=f'(x)dx$

с той лишь разницей, что формуле конечных приращений у нас дана формула нахождения истинного приращения $\Delta y$, но через производную $f'(c)$ в точке $c$, которая находится где-то между $a$ и $b$. Если же в формуле $\Delta y=f'(c)\Delta x$ устремить $\Delta x$ к нулю, то в пределе мы получим $dy=f'(x)dx$.

Приложения

• Теорема Лагранжа иногда может быть применена при раскрытии неопределённостей для нахождения пределов.

Вариации и обобщения

Теорема Лагранжа о конечных приращениях — одна из самых важных, узловая теорема во всей системе дифференциального исчисления. Она имеет массу приложений в вычислительной математике, и главнейшие теоремы математического анализа также являются её следствиями.

• Дифференцируемая на отрезке функция с производной, равной нулю, есть константа.

Доказательство. Для любых $x$ и $y$ существует точка $c$, такая что $f(y)-f(x)=f'(c)(y-x)=0$.

Значит, при всех $x$ и $y$ верно равенство $f(y)=f(x)$.

Замечание. Аналогично доказывается следующий важный критерий монотонности для дифференцируемых функций: Дифференцируемая функция $f(x)$ возрастает/убывает на отрезке $[a,b]$ тогда и только тогда, когда её производная $f'(x)$ на этом отрезке неотрицательна/неположительна. При этом строгая положительность/отрицательность производной влечёт строгую монотонность функции $f(x)$.

• Формула Тейлора с остаточным членом в форме Лагранжа). Если функция $f$ дифференцируема $n$ раз в окрестности точки $x$, то для малых $h$ (то есть тех, для которых отрезок $[x,x+h]$ лежит в указанной окрестности) справедлива формула Тейлора:

$f(x+h)=f(x)+f'(x)h+f''(x){\frac {h^{2}}{2}}+...+f^{(n-1)}(x){\frac {h^{n-1}}{(n-1)!}}+f^{(n)}(x+\theta h){\frac {h^{n}}{n!}}$

где $\theta$ — некоторое число из интервала $(0,1)$.

Замечание. Данное следствие является в то же время и обобщением. При $n=1$ из него получается сама теорема Лагранжа о конечных приращениях.

• Если функция $n$ переменных $f(x_{1},x_{2},\dots ,x_{n})$ дважды дифференцируема в окрестности точки О и все её вторые смешанные производные непрерывны в точке О, тогда в этой точке справедливо равенство:

${\frac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}={\frac {\partial ^{2}f}{\partial x_{j}\partial x_{i}}}$

Доказательство для $n=2$. Зафиксируем значения $\Delta x$ и $\Delta y$ и рассмотрим разностные операторы

$\Delta _{x}:f(x,y)\rightarrow {\frac {f(x+\Delta x,y)-f(x,y)}{\Delta x}}$ и $\Delta _{y}:f(x,y)\rightarrow {\frac {f(x,y+\Delta y)-f(x,y)}{\Delta y}}$.

По теореме Лагранжа существуют числа $\theta _{1},\theta _{2}\in (0,1)$, такие что

$\Delta _{y}\Delta _{x}f(x,y)=\Delta _{y}{\frac {\partial f}{\partial x}}(x+\theta _{1}\Delta x,y)={\frac {\partial }{\partial y}}{\frac {\partial f}{\partial x}}(x+\theta _{1}\Delta x,y+\theta _{2}\Delta y)\rightarrow {\frac {\partial }{\partial y}}{\frac {\partial f}{\partial x}}(x,y)$

при $(\Delta x,\Delta y)\rightarrow 0$ в силу непрерывности вторых производных функции $f(x,y)$.

Аналогично доказывается, что $\Delta _{x}\Delta _{y}f(x,y)\rightarrow {\frac {\partial }{\partial x}}{\frac {\partial f}{\partial y}}(x,y)$.

Но так как $\Delta _{y}\Delta _{x}f(x,y)=\Delta _{x}\Delta _{y}f(x,y)$, (что проверяется непосредственно), то эти пределы совпадают.

Замечание. Следствием этой формулы является тождество $d^{2}=0$ для оператора внешнего дифференциала, определённого на дифференциальных формах.

• Формула Ньютона — Лейбница. Если функция $f(x)$ дифференцируема на отрезке $[a,b]$ и её производная интегрируема по Риману на этом отрезке, то справедлива формула: $\int \limits _{a}^{b}f'(x)dx=f(b)-f(a)$.

Доказательство. Пусть $T$ — произвольное разбиение $a=x_{0}<x_{1}<x_{2}<...<x_{n}=b$ отрезка $[a,b]$. Применяя теорему Лагранжа, на каждом из отрезков $[x_{k-1},x_{k}]$ найдём точку $\xi _{k}$ такую, что $f'(\xi _{k})(x_{k}-x_{k-1})=f(x_{k})-f(x_{k-1})$.

Суммируя эти равенства, получим: $\sum \limits _{k=1}^{n}f'(\xi _{k})(x_{k}-x_{k-1})=\sum \limits _{k=1}^{n}(f(x_{k})-f(x_{k-1}))=f(b)-f(a)$

Слева стоит интегральная сумма Римана для интеграла $\int \limits _{a}^{b}f'(x)dx$ и заданного отмеченного разбиения. Переходя к пределу по диаметру разбиения, получим формулу Ньютона-Лейбница.

Замечание. Следствием (и обобщением) формулы Ньютона-Лейбница является формула Стокса, а следствием формулы Стокса является интегральная теорема Коши — основная теорема теории аналитических функций (ТФКП).

• Теорема об оценке конечных приращений. Пусть отображение $F:\Omega \rightarrow \mathbb {R} ^{m}$ непрерывно дифференцируемо в выпуклой компактной области $\Omega$ пространства $\mathbb {R} ^{n}$. Тогда $|F(y)-F(x)|\leq \sup \limits _{\xi \in \Omega }|DF(\xi )|\cdot |y-x|$.

Замечание. Без использования теоремы об оценке конечных приращений не обходятся доказательства таких теорем, как теорема об обратном отображении, теорема о неявной функции, теорема о существовании и единственности решения задачи Коши для обыкновенных дифференциальных уравнений.

См. также

• Лагранж, Жозеф Луи
• Теорема Коши — расширенный вариант этой теоремы.