Симметрия Фока в теории атома водорода

Квантовая задача Кулона (аналог классической задачи Кеплера), позволяющая рассчитывать спектр системы из двух противоположных зарядов, является до сих пор фундаментальной в квантовой теории. С ней связаны имена основателей физики 20-го века — Н. Бора, А. Зоммерфельда ,В. Паули, Э. Шредингера, В. Фока . С неё начинается введение в теорию атомных спектров и она прекрасно изучена методами теории специальных функций. Благодаря своей простоте и заложенной в ней симметрии — группе вращений 4-х мерного пространства SO(4), она является исключительно полезным и тонким инструментом теоретической физики для построения различных концепций. Реализацию симметрии SO(4) нашел В. Фок в импульсном пространстве. Результат Фока удивляет физиков: почему симметрия SO(4) проявляется в импульсном пространстве, свернутом в 3-d сферу c выходом в 4-d пространство.

Сущность открытия

Напомним предысторию достижения Фока. Два классических векторных интеграла — угловой момент и вектор Рунге-Ленца в квантовой механике соответствуют векторным операторам, которые коммутируют с оператором энергии, то есть с гамильтонианом. Анализ их коммутаторов, проведенный в, показывает, что они порождают алгебру Ли (линейное пространство с операцией коммутирования) совпадающую с алгеброй Ли малых (инфинитезимальных) операторов поворотов 4-х мерного пространства.

Для физиков это соответствие означает, что существует преобразование переменных и операторов, которое переводит исходную квантовую задачу Кулона в некоторое движение частицы на трехмерной 3-d сфере, вложенной в четырёхмерное 4-d пространство. Оператор энергии при этом будет инвариантен при вращениях 3-d сферы. Это напоминает замечательный эффект Л. Кэрола "с парящей улыбкой Чеширского кота ".

Подход Фока поразил современников.Исходным пунктом в его теории является интегральное уравнение Шредингера (УШ) в импульсном пространстве. Это пространство можно рассматривать как 3-d плоскость в 4-d пространстве. Затем Фок сворачивает её в сферу с помощью стереографической проекции, известной с античных времен как удобное преобразование глобуса на плоскую карту . (У Фока глобус трехмерный — также как и карта). При этом, Фок угадывает необходимый множитель для пси-функций, чтобы исходное интегральное уравнение перешло в уравнение для сферических функций на 3-d сфере (не путать со сферическими функциями на двумерной сфере). Это уравнение, редко используемое в физике, но известное в теории специальных функций, инвариантно относительно вращений в 4-d пространстве.

Фок не объясняет физический смысл найденного им преобразования. В результате остается принципиальный вопрос — почему симметрия SO(4) реализуется в свернутом импульсном, а не в координатном пространстве, и как электрон «узнал о стереографической проекции» . Позднее, Ефимов С. П. развил теорию В. Фока, с помощью переноса его результата в координатное пространство.. При этом переход от четырёхмерных сферических функций к функциям в физическом пространстве алгебраический (без интегралов) и сопровождается заменой четвёртой «лишней» координаты на мнимый радиус вектор $\imath r$.

Теория Фока

При использовании атомных единиц, когда единица энергии есть ${\frac {Z^{2}me^{4}}{\hbar ^{2}}}$, а единица длины равна радиусу Бора $a_{B}={\frac {\hbar ^{2}}{Zme^{2}}}$, УШ для собственных функций принимает вид:

$\left(-{\frac {1}{2}}\Delta -{\frac {1}{r}}\right)\Psi _{nlm}=-{\frac {1}{2n^{2}}}\Psi _{nlm}$.

Дапее удобно привести каждую орбиту с радиусом $na_{B}$ к единому радиусу, то есть заменить радиус вектор $\mathbf {r}$ на вектор ${\frac {\mathbf {r} }{n}}$. В результате УШ принимает обманчиво простую форму

$(-\Delta +1)\Psi _{nlm}(\mathbf {r} )={\frac {2n}{r}}\Psi _{nlm}(\mathbf {r} ),$

где используется снова обозначения $\mathbf {r}$ and $r$ для вектора и его модуля. В этом случае в импульсном представлении аргумент пси-функций растягивается: $\mathbf {p'} =n\mathbf {p}$.

При переходе в импульсное пространство, к собственным функциям УШ необходимо применить преобразование Фурье $(\hbar =1)$ :

$\Psi _{nlm}(\mathbf {r} )={\frac {1}{(2\pi )^{3}}}\int \ a_{nlm}(\mathbf {p} )e^{(i\mathbf {pr} )}d^{3}\mathbf {p}$.

Применение его к УШ приводит к свертке по импульсам. Потенциал ${\frac {1}{r}}$ переходит в функцию ${\frac {4\pi }{\left|\mathbf {p^{2}} \right|}}$, что дает интегральное (не локальное) уравнение:

$(\left|\mathbf {p^{2}} \right\|+1)a_{nlm}(\mathbf {p} )-{\frac {2n}{2\pi ^{2}}}\int {\frac {a_{nlm}(\mathbf {p'} )}{\left|\mathbf {p-p'} \right|^{2}}}d^{3}\mathbf {p'} .$

Отметим, что нелокальность уравнения приводит к тому, что Вектор Лапласа-Рунге-Ленца не фигурирует в импульсном пространстве.

Первый шаг теории Фока следующий: без всякого объяснения функция $a_{nlm}(\mathbf {p} )$ умножается на множитель $(1+\mathbf {p^{2}} )^{2}$.

Второй шаг : 3-d плоскость в импульсном пространстве сворачивается в 3-d сферу с координатами $({\boldsymbol {\xi }},{\mathit {\xi _{0}}})$ (см. рис.1)

Рис.1 Стереографическая проекция $3d$ $\mathbf {p}$-плоскости на $3d$ -сферу в 4d-пространстве

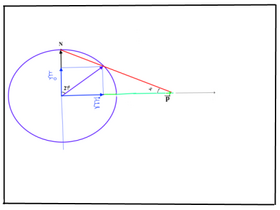
Из рисунка видно, что тангенс угла наклона проектирующей (красной) прямой равен:

$\tan \varphi ={\frac {1}{\left|\mathbf {p} \right|}}.$

Отсюда следуют формулы:

$\left|{\boldsymbol {\xi }}\right|=\sin 2\varphi ={\frac {2\left|\mathbf {p} \right|}{(1+\mathbf {p^{2}} )}},$

${\boldsymbol {\xi }}={\frac {2\mathbf {p} }{(1+\mathbf {p^{2}} )}},$

${\mathit {\xi _{0}}}=\cos 2\varphi ={\frac {(\mathbf {p^{2}} -1)}{(\mathbf {p^{2}} +1)}},$

${\boldsymbol {\xi }}^{2}+\xi _{0}^{2}=1.$

Стереографическая проекция удваивает угол наклона и в этом её эффект. Плоский рисунок при этом правильно отражает 4-х мерное преобразование.

В новых переменных, с учётом множителя Фока, собственная функция равна:

$b_{nlm}({\boldsymbol {\xi }},\xi _{0})=(\mathbf {p^{2}} +1)^{2}a_{nlm}(\mathbf {p} ).$

Существенно, что проекция является конформным преобразованием . Углы между пересекающимися кривыми сохраняются. Метрика на сфере в координатах пространства импульсов (плоскости p) равна:

${\frac {4}{\mathbf {(p^{2}+1)^{2}} }}(d\mathbf {p} )^{2}.$

Отсюда коэффициент сжатия элементов пространства p равен ${\frac {(\mathbf {p^{2}} +1)}{2}}$ . Элемент объёма в формуле (10) заменяем через элемент трехмерной поверхности :

$d^{3}\mathbf {p} ={\frac {1}{8}}(\mathbf {p^{2}} +1)^{3}dS_{\xi }$

Ядро интеграла удачно (и не очевидно) преобразуется следующим образом:

${\frac {1}{\mathbf {(p-p')^{2}} }}={\frac {2}{\mathbf {(p^{2}+1)} }}{\frac {1}{[{\boldsymbol {(\xi -\xi ')^{2}}}+(\xi _{0}-\xi '_{0})^{2}]}}{\frac {2}{\mathbf {(p'^{2}+1)} }},$

что не вытекает из конформности. Теперь подставляем последние три соотношения в интегральное уравнение . Получаем:

$b_{nlm}({\boldsymbol {\xi }},\xi _{0})-{\frac {n}{2\pi ^{2}\ }}\int {\frac {b_{nlm}({\boldsymbol {\xi '}},\xi '_{0})}{[{\boldsymbol {(\xi -\xi ')^{2}}}+(\xi _{0}-\xi '_{0})^{2}]}}dS_{\xi '},$

где, как видно из Рис.1, элемент поверхности на единичной сфере с объёмом $2\pi ^{2}$ равен:

$dS_{\xi }={\frac {d{\xi _{1}}d\xi _{2}d{\xi _{3}}}{\xi _{0}}}={\frac {dV_{\xi }}{\xi _{0}}}$

(Интегрирование по плоскому 3-d пространству удобно при расчетах.)

В. Фок далее отсылает к теории сферических функций в четырёхмерном пространстве, где полиномы Гегенбауэра играют важную роль. Однако, в найденное уравнение можно подставить любую сферическую функцию и их сумму с фиксированным значением индекса (n-1), которое соответствует значению n в исходном УШ. В силу этого, уравнение не определяет квантовые числа $l$ и $m$. Здесь важно свойство конформности. Повороту на сфере соответствует поворот на тот же угол в импульсном и координатном пространствах, так что функция с множителем $Y_{l,m}$ переходит в собственную функцию с тем же угловым множителем (но с изменённым аргументом).

Таким образом, необходимое решение интегрального уравнения на 3-d сфере равно

$b_{nlm}({\boldsymbol {\xi }},\xi _{0})=Y_{l,m}(\theta ,\varphi )G_{(n-1-l)}^{l+1}(\xi _{0})$,

где второй множитель есть полином Гегенбауэра.

Неадекватная интерпретация

Математические симметрии играют важную роль в теоретической физике, помогая лучше понять физическую природу явления. Например, материальная точка в осцилляторе движется «туда-сюда» на отрезке. Физики изобрели фазовую плоскость для координат $x,p$, где точка движется равномерно по окружности, а её проекция на ось $x$ есть движение в физическом пространстве. Подобная ситуация возникает в исследовании В. Фока. Математический аналог условно свободного движения возникает в импульсном 4-d пространстве.

В литературе встречается интерпретация результата Фока, в которой электрон в атоме водорода движется якобы свободно в 4-d пространстве на 3-d сфере. При этом наблюдатель из физического 3-d пространства видит проекцию этого движения. Этого утверждения в работе Фока нет, и такая интерпретация физически не адекватна.

См. также

• Метод Хартри — Фока
• Состояние Фока
• Пространство Фока
• Калибровка Фока-Швингера

Литература

• Fock, V.A. (2004) V.A. Fock-Selected Works:Quantum Mechanics and Quantum Field Theory. CRC Press.https://doi.org/10.1201/9780203643204