Додекаэдральные соты порядка 4
| Додекаэдральные соты порядка 4 | |
|---|---|

| |
| Тип | Гиперболические правильные соты |
| Символ Шлефли | {5,3,4} {5,31,1} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | {5,3} |
| Грани | Пятиугольники {5} |
| Рёберная фигура | квадраты {4} |
| Вершинная фигура |  Октаэдр |
| Двойственные соты | Кубические соты порядка 5[англ.] |
| Группа Коксетера | BH3, [5,3,4] DH3, [5,31,1] |
| Свойства | Regular, квазиправильные соты |
В гиперболическом трёхмерном пространстве додекаэдральные соты порядка 4 — это одна из четырёх компактных правильных заполняющих пространство мозаик (или сот). Имея символ Шлефли {5,3,4}, соты имеют четыре додекаэдра вокруг каждого ребра и 8 додекаэдров вокруг каждой вершины в октаэдральном расположении. Вершины сот строятся на 3 ортогональных осях. Двойственным телом сот являются кубические соты порядка 5[англ.].
Геометрические соты — это таким образом заполняющие пространство многогранные ячейки, что не остаётся свободных промежутков. Соты являются примером более общего математического понятия замощения в пространствах любой размерности.
Соты обычно строятся в обычном евклидовом («плоском») пространстве подобно выпуклым однородным сотам[англ.]. Они могут быть построены также в неевклидовых пространствах, такие как гиперболические однородные соты[англ.]. Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы образовать однородные соты на сферическом пространстве.
Описание
[править | править код]Двугранный угол додекаэдра равен ~116.6°, так что невозможно разместить 4 додекаэдра на ребре в евклидовом 3-мерном пространстве. Однако в гиперболическом пространстве для додекаэдра можно подобрать размер так, что его двугранные углы уменьшаются до 90 градусов, а тогда четыре додекаэдра точно заполняют пространство вокруг каждого ребра.
Симметрия
[править | править код]Соты строятся с половинной симметрией, {5,31,1}, с двумя типами (цветами) шестиугольных мозаик в построении Витхоффа. ![]()
![]()
![]()
![]()
![]()
![]()
![]() ↔
↔ ![]()
![]()
![]()
![]()
![]() .
.
Рисунки
[править | править код]
Связанные многогранники и соты
[править | править код]Существует четыре вида правильных компактных сот в гиперболическом 3D-пространстве:
 {5,3,4} |
 {4,3,5} |
 {3,5,3} |
 {5,3,5} |
Существует пятнадцать видов однородных сот[англ.] в семействе [5,3,4] групп Коксетера, включая эти правильные формы.
| {5,3,4} |
r{5,3,4} |
t{5,3,4} |
rr{5,3,4} |
t0,3{5,3,4} |
tr{5,3,4} |
t0,1,3{5,3,4} |
t0,1,2,3{5,3,4} |
|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

| |
| {4,3,5} |
r{4,3,5} |
t{4,3,5} |
rr{4,3,5} |
2t{4,3,5} |
tr{4,3,5} |
t0,1,3{4,3,5} |
t0,1,2,3{4,3,5} |
Существует одиннадцать видов однородных сот[англ.] в разветвлённом семействе [5,31,1] групп Коксетера, включая соты в чередующейся форме. Это построение может быть представлено чередованием (как на шахматной доске) с двумя цветами додекаэдральных ячеек.
Эти соты связаны также с 16-ячейником, кубическими сотами и шестиугольными мозаичными сотами порядка 4[англ.], все имеют октаэдральные вершинные фигуры:
| Правильные соты {p,3,4} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пространство | S3 | E3 | H3 | ||||||||
| Вид | Конечные | Аффинные | Компактные | Паракомпактные | Неокомпактные | ||||||
| Название | {3,3,4} |
{4,3,4} |
{5,3,4} |
{6,3,4} |
{7,3,4} |
{8,3,4} |
... {∞,3,4} | ||||
| Рисунок | 
|

|

|

|

|

|

| ||||
| Ячейки | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} | ||||
Эти соты являются частью последовательности четырёхмерных многогранников и сот с додекаэдральными ячейками:
| Пространство | S3 | H3 | |||||
|---|---|---|---|---|---|---|---|
| Вид | Конечные | Компактные | Паракомпактные | Неокомпактные | |||
| Название | {5,3,3} |
{5,3,4} |
{5,3,5} |
{5,3,6} |
{5,3,7} |
{5,3,8} |
... {5,3,∞} |
| Рисунок | 
|

|

|

|

|

|

|
| Vertex figure |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
Полноусечённые додекаэдральные соты порядка 4
[править | править код]| Полноусечённые додекаэдральные соты порядка 4 | |
|---|---|
| Тип | Однородные соты в гиперболическом пространстве[англ.] |
| Символ Шлефли | r{5,3,4} r{5,31,1} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | r{5,3} {3,4} |
| Грани | Треугольники {3} пятиугольники {5} |
| Вершинная фигура |  куб |
| Группа Коксетера | BH3, [5,3,4] DH3, [5,31,1] |
| Свойства | Вершинно транзитивные, рёберно транзитивные |
Полноусечённые додекаэдральные соты порядка 4', ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеют чередующиеся октаэдральные и икосододекаэдральные ячейки с кубом в качестве вершинной фигуры.
, имеют чередующиеся октаэдральные и икосододекаэдральные ячейки с кубом в качестве вершинной фигуры.

Связанные соты
[править | править код]Существует четыре вида полноусечённых компактных правильных сот:
| Рисунок | 
|

|

|

|
|---|---|---|---|---|
| Обозначение | r{5,3,4} |
r{4,3,5} |
r{3,5,3} |
r{5,3,5} |
| Вершинная фигура |

|

|
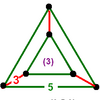
|

|
Усечённые додекаэдральные соты порядка 4
[править | править код]| Усечённые додекаэдральные соты порядка 4 | |
|---|---|
| Тип | Однородные соты в гиперболическом пространстве[англ.] |
| Символ Шлефли | t{5,3,4} t{5,31,1} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | t{5,3} {3,4} |
| Грани | Треугольники {3} десятиугольники {10} |
| Вершинная фигура |  Квадратная пирамида |
| Группа Коксетера | BH3, [5,3,4] DH3, [5,31,1] |
| Свойства | Вершинно транзитивные |
Усечённые додекаэдральные соты порядка 4, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеют октаэдральные и усечённые додекаэдральные ячейки с кубом в качестве вершинной фигуры.
, имеют октаэдральные и усечённые додекаэдральные ячейки с кубом в качестве вершинной фигуры.
Соты можно рассматривать как аналог двумерных гиперболических усечённых пятиугольных мозаик порядка 4[англ.] t{5,4} с гранями в виде усечённых пятиугольников и квадратов:
Связанные соты
[править | править код]| Рисунок | 
|

|

|

|
|---|---|---|---|---|
| Обозначение | t{5,3,4} |
t{4,3,5} |
t{3,5,3} |
t{5,3,5} |
| Вершинная фигура |

|

|

|

|
Биусечённые додекаэдральные соты порядка 4
[править | править код]| Биусечённые додекаэдральные соты порядка 4 Биусечённые кубические соты порядка 5 | |
|---|---|
| Тип | Однородные соты в гиперболическом пространстве[англ.] |
| Символ Шлефли | 2t{5,3,4} 2t{5,31,1} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | t{3,5} t{3,4} |
| Грани | Треугольники {3} квадраты {4} шестиугольники {6} |
| Вершинная фигура |  Тетраэдр |
| Группа Коксетера | BH3, [5,3,4] DH3, [5,31,1] |
| Свойства | Вершинно транзитивные |
Биусечённые додекаэдральные соты порядка 4 или биусечённые кубические соты порядка 5, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеют усечённые октаэдры и усечённые икосаэдры в качестве ячеек и тетраэдр в качестве вершинной фигуры.
, имеют усечённые октаэдры и усечённые икосаэдры в качестве ячеек и тетраэдр в качестве вершинной фигуры.
Связанные соты
[править | править код]| Рисунок | 
|

|

|
|---|---|---|---|
| Обозначение | 2t{4,3,5} |
2t{3,5,3} |
2t{5,3,5} |
| Вершинная фигура |

|

|

|
Скошенные додекаэдральные соты порядка 4
[править | править код]| Скошенные додекаэдральные соты порядка 4 | |
|---|---|
| Тип | Однородные соты в гиперболическом пространстве[англ.] |
| Символ Шлефли | rr{5,3,4} rr{5,31,1} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | rr{3,5} r{3,4} {}x{4} куб |
| Грани | Треугольники {3} квадраты {4} пятиугольники {5} |
| Вершинная фигура |  Треугольная призма |
| Группа Коксетера | BH3, [5,3,4] DH3, [5,31,1] |
| Свойства | Вершинно транзитивные |
Скошенные додекаэдральные соты порядка 4,![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеют ромбоикосододекаэдральные, кубооктаэдральные и кубические ячейки и треугольную призму в качестве вершинной фигуры.
, имеют ромбоикосододекаэдральные, кубооктаэдральные и кубические ячейки и треугольную призму в качестве вершинной фигуры.
Связанные соты
[править | править код]| Четыре вида скошенных правильных компактных сот в H3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Скошено-усечённые додекаэдральные соты порядка 4
[править | править код]| Скошено-усечённые додекаэдральные соты порядка 4 | |
|---|---|
| Тип | Однородные соты в гиперболическом пространстве[англ.] |
| Символ Шлефли | tr{5,3,4} tr{5,31,1} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | tr{3,5} t{3,4} {}x{4} Кубы |
| Грани | квадраты {4} шестиугольники {6} десятиугольники {10} |
| Вершинная фигура |  зеркальный сфеноид |
| Группа Коксетера | BH3, [5,3,4] DH3, [5,31,1] |
| Свойства | Вершинно транзитивные |
Скошено-усечённые додекаэдральные соты порядка 4 являются однородными сотами с диаграммой Коксетера — Дынкина ![]()
![]()
![]()
![]()
![]()
![]()
![]() и имеющие зеркальный сфеноид в качестве вершинной фигуры.
и имеющие зеркальный сфеноид в качестве вершинной фигуры.
Связанные соты
[править | править код]| Рисунок | 
|

|

|

|
|---|---|---|---|---|
| Обозначение | tr{5,3,4} |
tr{4,3,5} |
tr{3,5,3} |
tr{5,3,5} |
| Вершинная фигура |

|

|
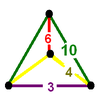
|

|
Струг-усечённые додекаэдральные соты порядка 4
[править | править код]| Струг-усечённые додекаэдральные соты порядка 4 | |
|---|---|
| Тип | Однородные соты в гиперболическом пространстве[англ.] |
| Символ Шлефли | t0,1,3{5,3,4} |
| Диаграммы Коксетера — Дынкина |
|
| Ячейки | t{5,3} rr{3,4} {}x{10} {}x{4} |
| Грани | Треугольники {3} квадраты {4} десятиугольники {10} |
| Вершинная фигура |  quad пирамида |
| Группа Коксетера | BH3, [5,3,4] |
| Свойства | Вершинно транзитивные |
Струг-усечённые додекаэдральные соты порядка 4 — однородные соты с диаграммой Коксетера — Дынкина ![]()
![]()
![]()
![]()
![]()
![]()
![]() и четырёхугольной пирамидой в качестве вершинной фигуры.
и четырёхугольной пирамидой в качестве вершинной фигуры.
Связанные соты
[править | править код]| Четыре вида струг-усечённых правильных компактных сот в H3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
См. также
[править | править код]- Выпуклые однородные соты в гиперболическом пространстве[англ.]
- Poincaré homology sphere Poincaré dodecahedral space
- пространство Зейферта — Вебера[англ.] Seifert–Weber dodecahedral space
- Список правильных многомерных многогранников и соединений
Примечания
[править | править код]Литература
[править | править код]- Coxeter. Tables I and II: Regular polytopes and honeycombs // Regular Polytopes[англ.]. — 3rd. ed.. — Dover Publications, 1973. — С. 294–296. — ISBN 0-486-61480-8.
- Coxeter. Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — С. 212-213. — ISBN 0-486-40919-8.
- Jeffrey R. Weeks. Chapter 16-17: Geometries on Three-manifolds I,II // The Shape of Space. — 2nd. — 2002. — ISBN 0-8247-0709-5.
- N.W. Johnson. Uniform Polytopes. — 1991. — (Manuscript).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
- N.W. Johnson. Chapter 13: Hyperbolic Coxeter groups // Geometries and Transformations. — 2015.
Для улучшения этой статьи желательно:
|




















