Апериодическое звено

Апериодическое звено — понятие, относящееся к теории автоматического управления. Типовое динамическое звено.

Апериодическое звено первого порядка

Апериодическое звено первого порядка — одноемкостное, инерционное звено, которое можно описать дифференциальным уравнением:

$a_{1}{\dot {y}}(t)+a_{0}y(t)=b_{0}x(t)$.

К стандартному виду приводится делением на $a_{0}$ правой и левой части уравнения:

$T{\dot {y}}(t)+y(t)=kx(t)$,

где:

• $y(t)$ — выходная величина;
• $x(t)$ — входная величина;
• $k={\frac {b_{0}}{a_{0}}}$ — коэффициент усиления звена;
• $T={\frac {a_{1}}{a_{0}}}$ — постоянная времени, характеризующая инерционность звена. Чем больше постоянная времени звена, тем дольше длится переходный процесс.

Временные характеристики

Переходная функция:

$h(t)=k(1-\mathrm {e} ^{-{\frac {t}{T}}})$

Весовая функция:

$w(t)={\frac {k}{T}}\mathrm {e} ^{-{\frac {t}{T}}}$

Передаточная функция

Передаточная функция апериодического звена 1-го порядка получается путём применения к дифференциальному уравнению свойства дифференцирования оригинала преобразования Лапласа:

$TsY(s)+Y(s)=kX(s)$,

АЧХ и ФЧХ апериодического звена 1-го порядка

$Y(s)[Ts+1]=X(s)k$.

$W(s)={\frac {Y(s)}{X(s)}}={\frac {k}{Ts+1}}$

Комплексная передаточная функция получается при подставлении вместо $s$ комплексной переменой $j\omega$.

Чтобы разделить на мнимую и действительную часть необходимо домножить числитель и знаменатель на комплексно-сопряженное число $(1-j\omega T)$:

$W(j\omega )={\frac {k}{1+j\omega T}}\cdot {\frac {1-j\omega T}{1-j\omega T}}={\frac {k-j\omega Tk}{1+\omega ^{2}T^{2}}}={\frac {k}{1+\omega ^{2}T^{2}}}-j{\frac {\omega Tk}{1+\omega ^{2}T^{2}}}$

$\mathrm {Re} \left\{W(j\omega )\right\}={\frac {k}{1+\omega ^{2}T^{2}}}$

$\mathrm {Im} \left\{W(j\omega )\right\}=-{\frac {\omega Tk}{1+\omega ^{2}T^{2}}}$

ЛАЧХ и ЛФЧХ апериодического звена 1-го порядка

АФЧХ

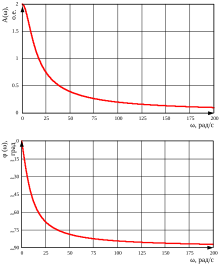
Амплитудная и фазовая частотные характеристики для заданной передаточной функции:

$W(s)={\frac {2}{0.1s+1}}$

ЛАФЧХ

Логарифмические амплитудная и фазовая частотные характеристики для заданной выше передаточной функции.

Из амплитудной характеристики видно, что колебания частот $\omega <{\frac {1}{T}}$ проходят через апериодическое звено 1-го порядка с отношением выходной и входной амплитуд близким к коэффициенту передачи звена $k$. Колебания частот $\omega >{\frac {1}{T}}$ проходят со значительным уменьшением амплитуды, следовательно «плохо пропускаются» звеном. Чем меньше постоянная времени $T$, а следовательно, чем меньше инерционность звена, тем более растянута амплитудная характеристика вдоль оси частот и больше полоса пропускания частот данного звена. Аналогично, в случае фазовой характеристики, чем меньше постоянная времени $T$, тем более растянута фазовая характеристика вдоль оси частот и меньше фазовые сдвиги между выходными и входными колебаниями. Угол отставания с увеличением частоты растет, а амплитуда колебаний на выходе падает. Предельный угол отставания равен -π/2.

После подачи на вход возмущающего воздействия отклонение выходной величины будет изменяться по экспоненте с максимальной скоростью в начальный момент. Затем скорость уменьшается до нуля, а выходная величина достигает нового установившегося значения.

В системах автоматического управления в качестве апериодического звена могут выступать двигатели постоянного тока, сопротивления и индуктивности, нагревательная камера, гидравлическая система с дросселем на выходе и др.

В целом считается, что почти любой объект управления в первом приближении, очень грубо, можно описать апериодическим звеном 1-го порядка.

Апериодическое звено второго порядка

Уравнение апериодического звена 2-го порядка имеет вид
$T_{2}^{2}{\frac {d^{2}x_{2}}{dt^{2}}}+T_{1}{\frac {dx_{2}}{dt}}+x_{2}=kx_{1}$,

Передаточная функция апериодического звена 2-го порядка:
$W(s)={\frac {k}{T_{2}^{2}s^{2}+T_{1}s+1}}$

Два последовательно соединенных апериодических звена 1-го порядка, могут быть представлены как апериодическое звено 2-го порядка с общим коэффициентом усиления.

Примеры применения

Одним из примеров апериодического звена первого порядка является RL – цепь, где входной величиной является напряжение U1, поступающее на цепь, а в качестве выходной величины может рассматриваться ток или напряжение U2 на сопротивлении R .В первом случае коэффициент передачи k = 1 / R, а во втором k = 1 Постоянная времени звена T = L / R.

См. также

• Система управления
• Автоматизация

Литература

• Бесекерский В.А., Попов Е.П. 4-е изд // Теория систем автоматического управления. — СПб.: Профессия, 2003. — 752 с. — ISBN 5-93913-035-6.
• Ким Д.П. 2-е изд // Теория автоматического управления. Т. 1. Линейные системы. — М.: ФИЗМАТЛИТ, 2007. — 312 с. — ISBN 978-5-9221-0857-7.