Циклоида

Запрос «Таутохронность»^[d] перенаправляется сюда. На эту тему нужно создать отдельную статью.

Точка на катящейся окружности рисует циклоиду

Цикло́ида (от греч. κυκλοειδής, «кругообразный») — плоская трансцендентная кривая.

Циклоида определяется кинематически как траектория фиксированной точки производящей окружности, катящейся без скольжения по прямой. Далее всюду $r$ обозначает радиус производящей окружности.

Уравнения

Основной источник:

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса $r$. Циклоида описывается:

• параметрически

  $x=rt-r\sin t$

  $y=r-r\cos t$.

• уравнением в декартовых координатах

  $x=r\arccos {\frac {r-y}{r}}-{\sqrt {2ry-y^{2}}}$.

• как решение дифференциального уравнения

  $\left({\frac {dy}{dx}}\right)^{2}={\frac {2r-y}{y}}$.

Свойства

Таутохронность циклоиды

Колебания с циклоидным регулятором.

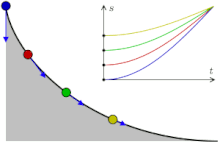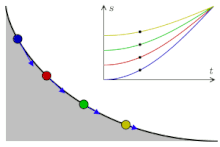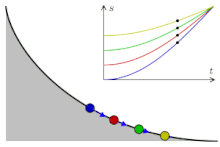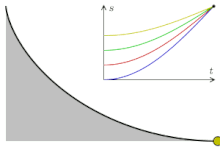
Циклоида — периодическая функция по оси абсцисс, с периодом $2\pi r$. За границы периода удобно принять особые точки (точки возврата) вида $t=2\pi k$, где $k$ — произвольное целое число.

У отдельной арки циклоиды есть ось симметрии, но нет центра симметрии.

Для проведения касательной к циклоиде в произвольной её точке $A$ достаточно соединить эту точку с верхней точкой производящей окружности. Соединив $A$ с нижней точкой производящей окружности, мы получим нормаль.

Длина арки циклоиды равна $8r$. Другими словами, длина одной ветви циклоиды равна учетверённому диаметру производящей окружности. Это свойство открыл Кристофер Рен в 1658 году

Зависимость длины дуги циклоиды ($s$) от параметра $t$ следующая: $s(t)=4r(1-\cos {t \over 2})$.

Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли сообщил, что этот факт Галилей открыл экспериментально: сравнил вес пластинок с кругом и с аркой циклоиды. Математически этот факт первым доказал Роберваль около 1634 года с помощью метода неделимых.

Радиус кривизны у первой арки циклоиды равен $4r\sin {\dfrac {t}{2}}$.

«Перевёрнутая» циклоида является кривой наискорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.

Два нижеследующих свойства, открытые Гюйгенсом, были им использованы для создания точных механических часов.

• Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды. Это непосредственное следствие таутохронности.
• Эволюта циклоиды является циклоидой, конгруэнтной исходной и параллельно сдвинутой от исходной так, что вершины переходят в «острия».

Площадь поверхности, образованной вращением арки циклоиды вокруг её основания, равна ${\dfrac {64}{3}}\pi r^{2}.$ Она превышает двойную площадь циклоиды (площадь осевого сечения) в $3{\dfrac {5}{9}}$ раза.

Вариации и обобщения

Циклоиду можно рассматривать как:

• разновидность трохоиды в случае, когда производящая окружность катится по прямой;
• предельный случай циклогона, когда число сторон многоугольника увеличивается до бесконечности.

Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые: циклоида, эпициклоида, гипоциклоида, трохоида, астроида (ср. построение лемнискаты Бернулли).

Исторический очерк

Первыми из учёных обратили внимание на циклоиду Николай Кузанский в XV веке и Шарль де Бовель в труде 1501 года. Но серьёзное исследование этой кривой началось только в XVII веке.

Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн. Среди трансцендентных кривых (то есть кривых, уравнение которых не может быть записано в виде многочлена от $x,y$), циклоида — первая из исследованных.

Паскаль писал о циклоиде:

Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса...

Оригинальный текст (фр.)

La Roulette est une ligne si commune, qu'apres la droitte, & la circulaire, il n'y en a point de si frequente; Et elle se décrit si fouuent aux yeux de tout le monde, qu'il y a lieu de s'estonner qu'elle n'ait point esté considerée par les anciens, dans lesquels on n'en trouue rien : Car ce n'est autre chose que le chemin que fait en l'air, le clou d'une rouë...

Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Якоб и Иоганн Бернулли и другие корифеи науки XVII—XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы математического анализа.

Тот факт, что аналитическое исследование циклоиды оказалось столь же успешным, как и анализ алгебраических кривых, произвёл большое впечатление и стал важным аргументом в пользу «уравнения в правах» алгебраических и трансцендентных кривых.

Применение

Один из самых популярных типов шестерёнок — с циклоидальными зубьями. Циклоидальные профили чаще встречаются в часовых механизмах.

Литература

• Берман Г. Н. Циклоида. М., Наука, 1980, 112 с.
• Выгодский М. Я. Справочник по высшей математике. — М.: АСТ, 2019. — 704 с. — ISBN 978-5-17-117741-6.
• Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 126-165. — ISBN 5-900916-83-9.
• Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, М: Наука 1978, стр. 32.
• Циклоида : [арх. 3 января 2023] // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
• Циклоида // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5. — Стб. 817.

Ссылки

• Веров С. Г. Тайны циклоиды // Квант. — 1975. — № 8. — С. 19—27.