Критерий Конвея


Критерий Конвея — набор условий, при выполнении которых протоплитка[англ.] замощает плоскость. Назван по имени английского математика Джона Хортона Конвея[1]. Выполнение критерия Конвея является достаточным, но не обязателеным условием для замощения плоскости.
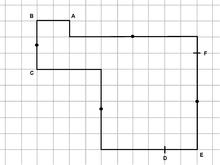
Согласно критерию, плитка должна быть замкнутым топологическим диском[англ.] с шестью последовательными точками A, B, C, D, E и F на границе и должны выполняться следующие условия:
- часть границы от A до B совместима параллельным переносом с частью от E до D;
- каждая из частей границы BC, CD, EF и FA центрально симметрична, то есть, каждая из них совпадает с собой при вращении на 180° относительно средней точки;
- некоторые из шести точек могут совпадать, но, по меньшей мере, три из них должны быть различными[2].
Любая протоплитка, удовлетворяющая критериям Конвея, допускает периодическое замощение плоскости, при этом используется только параллельный перенос и вращение на 180°. Критерий Конвея является достаточным условием для доказательства, что протоплитка замощает плоскость, но не является необходимым условием — существуют плитки, не удовлетворяющие критерию, но замощающие плоскость[3].
Примеры
[править | править код]Простейшая формулировка критерия утверждает, что любой шестиугольник, у которого противоположные стороны параллельны и равны по длине, замощает плоскость с использованием только параллельного переноса. Такие фигуры называются параллелогонами[4]. Если же некоторые точки совпадают, критерий может быть применён к другим многоугольникам и даже к фигурам с кривой в качестве периметра[5].
Критерий Конвея способен различить много фигур, в частности полиформы — за исключением двух нонамино справа, все замощающие плоскость полимино вплоть до нонамино могут образовать по меньшей мере одну плитку, удовлетворяющую критерию Конвея[3]. Две плитки нонамино показывают, что критерий Конвея достаточен, но не обязателен для замощения плоскости.
Примечания
[править | править код]- ↑ Schattschneider, 1980, с. 224-233.
- ↑ Периодическая мозаика: общие многоугольники. Дата обращения: 17 января 2017. Архивировано 20 мая 2014 года.
- ↑ 1 2 Rhoads, 2005, с. 329–353.
- ↑ Martin, 1991, с. 152.
- ↑ Пять типов плиток для критерия Конвея Архивировано 6 июля 2012 года., PDF
Литература
[править | править код]- Doris Schattschneider. Will It Tile? Try the Conway Criterion! // Mathematics Magazine. — 1980. — Т. 53.
- Glenn C. Rhoads,. Planar tilings by polyominoes, polyhexes, and polyiamonds // Journal of Computational and Applied Mathematics. — 2005. — Т. 174, вып. 2, 15 (Feb 15).
- George Martin. Polyominoes: A Guide to Puzzles and Problems in Tiling. — Washington, DC: Mathematical Association of America, 1991. — (Spectrum). — ISBN 0883855011.
Ссылки
[править | править код]- History and introduction to polygon models, polyominoes and polyhedra, by Anthony J Guttmann
- G C Rhoads. Planar tilings by polyominoes, polyhexes, and polyiamonds, // Journal of Computational and Applied Mathematics. — 2005. — Т. 174 p. — С. 329-353.