跳转到内容

連續函數 (拓撲學)：修订间差异

维基百科，自由的百科全书
以互动方式浏览历史
←上一版本
删除的内容 添加的内容
可视化wikitext
AlleborgoBot（留言 | 贡献）
34,640次编辑
添加{{merge to}}标记到条目
 
（未显示15个用户的19个中间版本）
第1行： 第1行：
{{merge to|连续函数|time=2018-01-04T05:04:19+00:00}}
{{translating|tfrom=[[:en:Continuous function (topology)]]|tpercent=10}}
{{unreferenced|time=2015-09-23T15:31:30+00:00}}
在[[拓撲學]]和[[數學]]的相關領域裡，'''連續函數'''是指在[[拓撲空間]]之間的一種[[態射]]。直觀上來說，其為一個函數''f''，其中每一群在''f(x)''附近的點都會含有在''x''附近的一群點之[[值域|值]]。對一個一般的拓撲空間來說，這是指''f(x)''的[[鄰域]]總會包含著''x''之鄰域的值。
在[[拓撲學]]和[[數學]]的相關領域裡，'''連續函數'''是指在[[拓撲空間]]之間的一種[[態射]]。直觀上來說，其為一個函數''f''，其中每一群在''f(x)''附近的點都會含有在''x''附近的一群點之[[值域|值]]。對一個一般的拓撲空間來說，這是指''f(x)''的[[鄰域]]總會包含著''x''之鄰域的值。


第14行： 第15行：
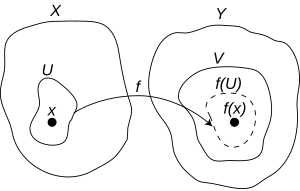
以前像為基底之定義時常很難直接地被使用。替代地，設有一由''X''至''Y''的函數''f''，其中的''X''和''Y''都是拓撲空間。則''f''會被稱為是'''在''x''為連續的'''，其中''x''為''X''的元素，若對於任一''f''(''x'')的[[鄰域]]''V''，都存在一個能使<math>f(U) \subseteq V</math>之''x''的鄰域''U''。雖然此一定義看起來很複雜，其在直覺上是指不論''V''變得多「小」，總會可以找到一個包含可映射至''V''內之''x''的''U''。若''f''在''X''內的每一個元素''x''都會連續，則簡稱''f''是連續的。
以前像為基底之定義時常很難直接地被使用。替代地，設有一由''X''至''Y''的函數''f''，其中的''X''和''Y''都是拓撲空間。則''f''會被稱為是'''在''x''為連續的'''，其中''x''為''X''的元素，若對於任一''f''(''x'')的[[鄰域]]''V''，都存在一個能使<math>f(U) \subseteq V</math>之''x''的鄰域''U''。雖然此一定義看起來很複雜，其在直覺上是指不論''V''變得多「小」，總會可以找到一個包含可映射至''V''內之''x''的''U''。若''f''在''X''內的每一個元素''x''都會連續，則簡稱''f''是連續的。


<center>[[image:continuity_topology.svg|300px|一函數在一點的連續性]]</center>
<center>[[File:continuity_topology.svg|300px|一函數在一點的連續性]]</center>


在一[[度量空間]]內，則其會等價於將所有鄰域替換成考量以''x''和''f''(''x'')為中心之[[球 (數學)|開球]]的[[鄰域系統]]。這會導致在實分析中對[[連續函數]]的標準定義，其敘述著一個函數若為連續時，則其靠近''x''的所有點都會映射至靠近''f''(''x'')的點上。這只在度量空間中有意義，因為只有在度量空間中有距離的概念。
在一[[度量空間]]內，則其會等價於將所有鄰域替換成考量以''x''和''f''(''x'')為中心之[[球 (數學)|開球]]的[[邻域系统]]。這會導致在實分析中對[[連續函數]]的標準定義，其敘述著一個函數若為連續時，則其靠近''x''的所有點都會映射至靠近''f''(''x'')的點上。這只在度量空間中有意義，因為只有在度量空間中有距離的概念。


===數列和網===
===數列和網===
在一些文章中，空間的拓撲會被簡便地以[[極限點]]來描述。
在一些文章中，空間的拓撲會被簡便地以[[極限點]]來描述。
In many instances, this is accomplished by specifying when a point is the [[limit of a sequence]], but for some spaces that are too large in some sense, one specifies also when a point is the limit of more general sets of points indexed by a [[directed set]], known as [[net (mathematics)|nets]]. A function is continuous only if it takes limits of sequences to limits of sequences. In the former case, preservation of limits is also sufficient; in the latter, a function may preserve all limits of sequences yet still fail to be continuous, and preservation of nets is a necessary and sufficient condition.


{{点集拓扑}}
In detail, a function ''f'' : ''X'' &rarr; ''Y'' is '''sequentially continuous''' if whenever a sequence (''x''<sub>''n''</sub>) in ''X'' converges to a [[limit of a sequence|limit]] ''x'', the sequence (''f''(''x''<sub>''n''</sub>)) converges to ''f''(''x''). Thus sequentially continuous functions "preserve sequential limits". Every continuous function is sequentially continuous. If ''X'' is a [[first-countable space]], then the converse also holds: any function preserving sequential limits is continuous. In particular, if ''X'' is a metric space, sequential continuity and continuity are equivalent. For non first-countable spaces, sequential continuity might be strictly weaker than continuity. (The spaces for which the two properties are equivalent are called [[sequential space]]s.) This motivates the consideration of [[net (mathematics)|nets]] instead of sequences in general topological spaces. Continuous functions preserve limits of nets, and in fact this property characterizes continuous functions.


⚫
[[Category:拓扑学|L]]
=== Closure operator definition ===
[[Category:连续映射|L]]
Given two topological spaces (''X'',cl) and (''X''&nbsp;' ,cl&nbsp;') where cl and cl&nbsp;' are two [[closure operator]]s then a function
:<math>f:(X,\mathrm{cl}) \to (X' ,\mathrm{cl}')</math>
is '''continuous''' if for all subsets ''A'' of ''X''
:<math>f(\mathrm{cl}(A)) \subseteq \mathrm{cl}'(f(A)).</math>

One might therefore suspect that given two topological spaces (''X'',int) and (''X''&nbsp;' ,int&nbsp;') where int and int&nbsp;' are two [[interior operator]]s then a function
:<math>f:(X,\mathrm{int}) \to (X' ,\mathrm{int}')</math>
is '''continuous''' if for all subsets ''A'' of ''X''
:<math>f(\mathrm{int}(A)) \subseteq \mathrm{int}'(f(A))</math>
or perhaps if
:<math>f(\mathrm{int}(A)) \supseteq \mathrm{int}'(f(A));</math>
however, neither of these conditions is either necessary or sufficient for continuity.

Instead, we must resort to inverse images: given two topological spaces (''X'',int) and (''X''&nbsp;' ,int&nbsp;') where int and int&nbsp;' are two [[interior operator]]s then a function
:<math>f:(X,\mathrm{int}) \to (X' ,\mathrm{int}')</math>
is '''continuous''' if for all subsets ''A'' of ''X''
:<math>f^{-1}(\mathrm{int}(A)) \subseteq \mathrm{int}'(f^{-1}(A)).</math>
We can also write that given two topological spaces (''X'',cl) and (''X''&nbsp;' ,cl&nbsp;') where cl and cl&nbsp;' are two [[closure operator]]s then a function
:<math>f:(X,\mathrm{cl}) \to (X' ,\mathrm{cl}')</math>
is continuous if for all subsets ''A'' of ''X''
:<math>f^{-1}(\mathrm{cl}(A)) \supseteq \mathrm{cl}'(f^{-1}(A)).</math>

=== Closeness relation definition ===
Given two topological spaces (''X'',&delta;) and (''X''&nbsp;' ,&delta;&nbsp;') where &delta; and &delta;&nbsp;' are two [[closeness relation]]s then a function
:<math>f:(X,\delta) \to (X' ,\delta')</math>
is '''continuous''' if for all points ''x'' and ''y'' of ''X''
:<math>x \delta y \Leftrightarrow f(x)\delta'f(y).</math>

== Useful properties of continuous maps ==
Some facts about continuous maps between topological spaces:
* If ''f'' : ''X'' &rarr; ''Y'' and ''g'' : ''Y'' &rarr; ''Z'' are continuous, then so is the composition ''g'' o ''f'' : ''X'' &rarr; ''Z''.
* If ''f'' : ''X'' &rarr; ''Y'' is continuous and
** ''X'' is [[Compact space|compact]], then ''f''(''X'') is compact.
** ''X'' is [[Connected space|connected]], then ''f''(''X'') is connected.
** ''X'' is [[Connected space|path-connected]], then ''f''(''X'') is path-connected.

== Other notes ==
If a set is given the [[discrete topology]], all functions with that space as a domain are continuous. If the domain set is given the [[indiscrete topology]] and the range set is at least [[T0 space|T<sub>0</sub>]], then the only continuous functions are the constant functions. Conversely, any function whose range is indiscrete is continuous.

Given a set ''X'', a [[partial ordering]] can be defined on the possible [[topology|topologies]] on ''X''. A continuous functions between two topological spaces stays continuous if we [[stronger topology|strengthen]] the topology of the [[domain space]] or [[weaker topology|weaken]] the topology of the [[codomain space]]. Thus we can consider the continuity of a given function a [[topological property]], depending only on the topologies of its domain and codomain spaces.

For a function ''f'' from a topological space ''X'' to a set ''S'', one defines the [[final topology]] on ''S'' by letting the open sets of ''S'' be those subsets ''A'' of ''S'' for which ''f<sup>-1</sup>(A)'' is open in ''X''. If ''S'' has an existing topology, ''f'' is continuous with respect to this topology if and only if the existing topology is [[Comparison of topologies|coarser]] than the final topology on ''S''. Thus the final topology can be characterized as the finest topology on ''S'' which makes ''f'' continuous. If ''f'' is [[surjective]], this topology is canonically identified with the [[quotient topology]] under the [[equivalence relation]] defined by ''f''. This construction can be generalized to an arbitrary family of functions ''X'' → ''S''.

Dually, for a function ''f'' from a set ''S'' to a topological space, one defines the [[initial topology]] on ''S'' by letting the open sets of ''S'' be those subsets ''A'' of ''S'' for which ''f''(''A'') is open in ''X''. If ''S'' has an existing topology, ''f'' is continuous with respect to this topology if and only if the existing topology is finer than the initial topology on ''S''. Thus the initial topology can be characterized as the coarsest topology on ''S'' which makes ''f'' continuous. If ''f'' is injective, this topology is canonically identified with the [[subspace topology]] of ''S'', viewed as a subset of ''X''. This construction can be generalized to an arbitrary family of functions ''S'' → ''X''.

Symmetric to the concept of a continuous map is an [[open map]], for which ''images'' of open sets are open. In fact, if an open map ''f'' has an inverse, that inverse is continuous, and if a continuous map ''g'' has an inverse, that inverse is open.

If a function is a [[bijection]], then it has an [[inverse function]]. The inverse of a continuous bijection is open, but need not be continuous. If it is, this special function is called a [[homeomorphism]].
If a continuous bijection has as its domain a [[compact space]] and its codomain is [[Hausdorff space|Hausdorff]], then it is automatically a homeomorphism.

⚫
[[Category:連續映射| ]]

[[cs:Spojité zobrazení]]
[[de:Stetigkeit (Topologie)]]
[[en:Continuous function (topology)]]
[[he:רציפות (טופולוגיה)]]
[[ko:연속함수 (위상수학)]]

2018年1月4日 (四) 05:04的最新版本

在拓撲學和數學的相關領域裡，連續函數是指在拓撲空間之間的一種態射。直觀上來說，其為一個函數f，其中每一群在f(x)附近的點都會含有在x附近的一群點之值。對一個一般的拓撲空間來說，這是指f(x)的鄰域總會包含著x之鄰域的值。

在一個度量空間(如實數)裡，這是指在f(x)一定距離內的點總會包含著在x某些距離內的所有點。

定義

[编辑]

因為有若干個對拓撲結構的等價定義存在，所以亦存在若干種定義連續函數的方法。

開集與閉集定義

[编辑]

拓撲中最常見的連續概念之定義為將其定義為一個其開集之前像亦為開集的函數。類似開集的公式化，亦有一閉集公式化，其將連續函數定義為其閉集之前像亦為閉集的函數。

鄰域定義

[编辑]

以前像為基底之定義時常很難直接地被使用。替代地，設有一由X至Y的函數f，其中的X和Y都是拓撲空間。則f會被稱為是在x為連續的，其中x為X的元素，若對於任一f(x)的鄰域V，都存在一個能使之x的鄰域U。雖然此一定義看起來很複雜，其在直覺上是指不論V變得多「小」，總會可以找到一個包含可映射至V內之x的U。若f在X內的每一個元素x都會連續，則簡稱f是連續的。

一函數在一點的連續性

在一度量空間內，則其會等價於將所有鄰域替換成考量以x和f(x)為中心之開球的邻域系统。這會導致在實分析中對連續函數的標準定義，其敘述著一個函數若為連續時，則其靠近x的所有點都會映射至靠近f(x)的點上。這只在度量空間中有意義，因為只有在度量空間中有距離的概念。

數列和網

[编辑]

在一些文章中，空間的拓撲會被簡便地以極限點來描述。

检索自“https://zh.wikipedia.org/zhwiki/w/index.php?title=連續函數_(拓撲學)&oldid=47657832”