面积矩:修订间差异
外观
删除的内容 添加的内容
WikitanvirBot(留言 | 贡献) 小 r2.7.1) (機器人 新增: fa:گشتاور نخست سطح |
小 撤销180.217.34.12(讨论)的版本68604539 标签:撤销 |
||
| (未显示8个用户的10个中间版本) | |||
| 第1行: | 第1行: | ||
{{unreferenced|time=2018-09-23T02:28:54+00:00}} |
|||
| ⚫ | |||
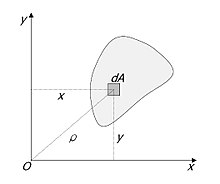
[[File:PolarMomentOfInertia.jpg|right|thumb|微面積為<math>dA_i</math> <br /> <math>x_i</math>及<math>y_i</math>為微面積與坐標系統的距離]] |
|||
| ⚫ | |||
<math>J=\iint_{S} \rho ds</math> |
<math>J=\iint_{S} \rho ds</math> |
||
其中:<math>\rho</math>为微元距轴的距离 |
其中:<math>\rho</math>为微元距轴的距离 |
||
==定義== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
面积一次矩也會用<math>Q</math>表示。 |
|||
| ⚫ | |||
:<math> |
|||
| ⚫ | |||
</math> |
|||
:<math> |
|||
| ⚫ | |||
</math> |
|||
==形心== |
|||
| ⚫ | |||
一個面積的形心便是: |
|||
:<math>\bar x =\frac {S_x}{A} = \frac {\int_A x dA} {\int dA}</math> |
|||
:<math>\bar y = \frac {S_y}{A} = \frac {\int_A y dA} {\int dA}</math> |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
[[da:Modstandsmoment]] |
|||
[[de:Flächenmoment]] |
|||
[[en:First moment of area]] |
|||
[[es:Primer momento de área]] |
|||
[[fa:گشتاور نخست سطح]] |
|||
[[fr:Moment statique]] |
|||
[[hu:Elsőrendű nyomaték]] |
|||
[[it:Momento statico]] |
|||
[[nl:Statisch moment]] |
|||
[[no:Statisk moment]] |
|||
[[pl:Moment statyczny pola]] |
|||
[[uk:Статичний момент плоскої фігури]] |
|||