配对函数:修订间差异
外观
删除的内容 添加的内容
Symplectopedia(留言 | 贡献) 小 快速增加分类“函数”(通过HotCat) |
小 →康托尔配对函数 |
||
| (未显示10个用户的14个中间版本) | |||
| 第1行: | 第1行: | ||
在[[数学]]中,'''配对函数'''是 |
在[[数学]]中,'''配对函数'''是一种将两个[[自然数]]唯一地编码成一个自然数的过程。 |
||
在[[集合论]]中可以用任何配对函数来证明[[整数]]和[[有理数]]有同自然数相同的[[基数]]。在[[理论计算机科学]]中用它们把定义在自然数的向量上函数 |
在[[集合论]]中可以用任何配对函数来证明[[整数]]和[[有理数]]有同自然数相同的[[基数 (数学)|基数]]。在[[理论计算机科学]]中用它们把定义在自然数的向量上的函数<math>f : \mathbb{N}^{k} \rightarrow \mathbb{N}</math>编码成一个新函数<math>g: \mathbb{N} \rightarrow \mathbb{N}</math>。 |
||
==定义== |
== 定义 == |
||
'''配对函数'''是[[双射]]函数 |
'''配对函数'''是一种可计算的[[双射]]函数 |
||
:<math>\pi:\mathbb{N} \times \mathbb{N} \to \mathbb{N}</math> 。 |
:<math>\pi:\mathbb{N} \times \mathbb{N} \to \mathbb{N}</math> 。 |
||
==康托尔配对函数== |
== 康托尔配对函数 == |
||
[[ |
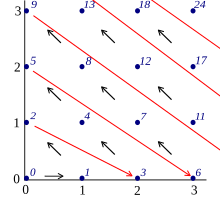
[[File:Pairing natural.svg|thumb|康拖尔配对函数。]] |
||
| ⚫ | |||
| ⚫ | |||
:<math>\pi:\mathbb{N} \times \mathbb{N} \to \mathbb{N}</math> |
:<math>\pi:\mathbb{N} \times \mathbb{N} \to \mathbb{N}</math> |
||
定义为 |
定义为 |
||
| 第18行: | 第19行: | ||
在应用配对函数到 <math>k_1</math> 和 <math>k_2</math> 的时候,我们经常指示结果的数为 <math>\langle k_1, k_2 \rangle</math> |
在应用配对函数到 <math>k_1</math> 和 <math>k_2</math> 的时候,我们经常指示结果的数为 <math>\langle k_1, k_2 \rangle</math> |
||
可以把上面的函數以[[递归定义|遞迴定義]]推廣成以下的'''康托尔元组函数''' |
|||
:<math>\pi^{(n)}:\mathbb{N}^n \to \mathbb{N}</math> |
:<math>\pi^{(n)}:\mathbb{N}^n \to \mathbb{N}</math> |
||
定義為 |
|||
作为 |
|||
:<math>\pi^{( |
:<math>\pi^{(2)}(k_1,\,k_2)=\pi(k_1,\,k_2)</math> |
||
:<math>\pi^{(n)}(k_1,\,\ldots, k_{n-1},\,k_n) := \pi [\,\pi^{(n-1)}(k_1,\,\ldots,\,k_{n-1}),\,k_n\,]</math> |
|||
==外部链接== |
|||
*[http://mathworld.wolfram.com/PairingFunction.html "Pairing function" at Mathworld] |
|||
== 引用 == |
|||
*{{mathworld|urlname=PairingFunction|author=Steven Pigeon|title=Pairing function}} |
|||
[[Category:集合论|P]] |
[[Category:集合论|P]] |
||
[[Category:函数]] |
[[Category:函数]] |
||
[[de:Cantorsche Paarungsfunktion]] |
|||
[[en:Pairing function]] |
|||
[[it:Funzione coppia]] |
|||
[[ja:対関数]] |
|||










![{\displaystyle \pi ^{(n)}(k_{1},\,\ldots ,k_{n-1},\,k_{n}):=\pi [\,\pi ^{(n-1)}(k_{1},\,\ldots ,\,k_{n-1}),\,k_{n}\,]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/425c9a6ba21bed327326ac812972ad7ee2540bc7)