球面:修订间差异
小 →公式: 改两个字,以原条目名为准 |
无编辑摘要 |
||
| (未显示12个用户的41个中间版本) | |||
| 第1行: | 第1行: | ||
{{General geometry}} |
|||
[[File:Sphere wireframe 10deg 10r.svg|right|thumb|一個球面。]] |
|||
'''球面''' ({{lang-en|sphere}})是[[立体几何|三维空间]]中完全圆形的[[几何学|几何]]物体,它是[[球 (数学)|圆球]]的表面(类似于在二维空间中,“[[圆]] ”包围着“[[圆盘]]”那样)。 |
|||
'''球面'''是在三維幾何空間內理想的[[對稱]]面。[[數學]]将其定义为一個'''[[球體]]'''的[[表面]]或是[[邊界 (拓撲學)|邊界]]。但是在数学之外,它只是三维空間中一個球的表面。 |
|||
就像在二维空间中的圆的定义一样,球面在数学上定义为三维空间中离给定的点距离相同的[[轨迹|点的集合]] {{math|''r''}}。 <ref name="Albert54">{{harvnb|Albert|2016|loc=p. 54}}</ref> 这个距离 {{math|''r''}} 是球的[[半径]] ,球(ball)则是由离给定点距离小于 {{math|''r''}} 的所有点构成的几何体,而这个给定点就是球心。球的半径和球心也是球面的半径和中心。两端都在球面上的最长线段通过球心,其长度是其半径的两倍;它是球面和球体的[[直径]] 。 |
|||
== 幾何學 == |
|||
在[[立體幾何|三維空間]]、[[歐幾里得幾何|歐幾里得]]、[[幾何學]],'''球面'''被設定為是在'''R'''<sup>3</sup>空間中與一個定點距離為r的所有點的集合,此處r是一個正的[[實數]],稱為'''[[半徑]]''',固定的點稱為'''[[球心]]'''或'''中心''',並且不屬於'''球面'''的範圍。'''r''' = 1是球的特例,稱為'''[[單位球]]'''。 |
|||
尽管在数学之外,术语“球面”和“球”有时可互换使用,但在[[数学]]中是明确区分的:''球面''是一种嵌在三维[[欧几里得空间]]内的二维封闭曲面,而''球''是一种三维图形,其包括球面和球面''内部''的一切('''闭球'''),不过更常见的定义是只包括球面''内部''的所有点,''不包括''球面上的点('''开球''')。这种区别并不总是保持不变,尤其是在旧的数学文献里,sphere(球面)被当作固体。这与在[[平面 (数学)|平面]]上混用术语“圆”(circle)和“圆盘”(disk)的情况类似。 |
|||
=== 公式 === |
|||
在[[解析幾何]]中,球面是球心在<math>(x_0,y_0,z_0)</math>,半径是''r''的所有坐标为(''x'', ''y'', ''z'')的点的集合: |
|||
==三维空间中的方程== |
|||
:<math>(x - x_0 )^2 + (y - y_0 )^2 + ( z - z_0 )^2 = r^2 \,</math>. |
|||
{{see also|三角函数|球座標系}} |
|||
在[[解析几何]]中,球心为 {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>, ''z''<sub>0</sub>)}},半径为 {{mvar|r}} 的球面是满足下面方程的所有点 {{math|(''x'', ''y'', ''z'')}} 的[[轨迹]] |
|||
使用[[极坐標]]來表示半徑為''r''的球面: |
|||
:<math> (x - x_0 )^2 + (y - y_0 )^2 + ( z - z_0 )^2 = r^2.</math> |
|||
令 {{mvar|a, b, c, d, e}} 为实数,{{math|''a'' ≠ 0}},并且 |
|||
:<math> x = x_0 + r \sin \theta \; \cos \phi </math> |
|||
:<math> |
:<math>x_0 = \frac{-b}{a}, \quad y_0 = \frac{-c}{a}, \quad z_0 = \frac{-d}{a}, \quad \rho = \frac{b^2 +c^2+d^2 - ae}{a^2}. </math> |
||
如果 <math>\rho < 0</math>,则那么下面的方程 |
|||
:<math>f(x,y,z) = a(x^2 + y^2 +z^2) + 2(bx + cy + dz) + e = 0</math> |
|||
没有实数根,称为'''虚球面'''的方程。如果 <math>\rho = 0</math>,则 <math>f(x,y,z) = 0</math> 的唯一解是点 <math>P_0 = (x_0,y_0,z_0)</math>,此时该方程称作'''点球面'''的方程。还有一种,就是在 <math>\rho > 0</math> 的情况下,<math>f(x,y,z) = 0</math> 是球面的方程,其中心是<math>P_0</math>,半径是<math>\sqrt \rho</math>。<ref name="Albert54"></ref> |
|||
如果上述等式中的 {{mvar|a}} 是零,那么 {{math|1=''f''(''x'', ''y'', ''z'') = 0}} 就成为了平面方程。因此,平面可以认为是球心在[[无穷远点]]的球面。<ref name="Woods266">{{harvnb|Woods|1961|loc=p. 266}}</ref> |
|||
(可以參考[[三角函數]]和[[球坐標]]) |
|||
半径 <math>r > 0</math>,中心在 <math>(x_0,y_0,z_0)</math> 的球面上的点可以写成参数方程 |
|||
:<math>\begin{align} x &= x_0 + r \sin \varphi \; \cos \theta \\ |
|||
y &= y_0 + r \sin \varphi \; \sin \theta \qquad (0 \leq \varphi \leq \pi,\; 0 \leq \theta < 2\pi ) \\ |
|||
z &= z_0 + r \cos \varphi \,\end{align}</math><ref>{{harvtxt|Kreyszig|1972|p=342}}</ref> |
|||
以原点为中心的任意半径的球面是以下[[微分形式]]的积分曲面: |
|||
:<math> x \, dx + y \, dy + z \, dz = 0</math> |
|||
:<math> x \,\mathrm{d}x + y \, \mathrm{d}y + z \, \mathrm{d}z = 0.</math> |
|||
这个方程反映了在球面上行进的点的位置 {{math|(''x'', ''y'', ''z'')}} 和速度向量 {{math|(''dx'', ''dy'', ''dz'')}} 总是彼此[[正交]]的。 |
|||
球面还可以通过以任何[[直径]]为轴,把圆旋转[[圆|一周]]形成的表面来构造。由于圆是一种特殊的[[椭圆]] ,所以球面也是一种特殊的椭球面。椭圆围绕其长轴旋转形成的曲面,就是[[類球面|长球面]];如果绕短轴旋转,就会形成一个扁球面。<ref>{{harvnb|Albert|2016|loc=p. 60}}</ref> |
|||
半徑為''r''的球面面積為: |
|||
==包围的体积 == |
|||
:<math>A = 4 \pi r^2 \,</math> |
|||
[[File:Esfera Arquímedes0.svg|thumb|将圆柱外接到一个球面上]] |
|||
在三维中,球面内包围的[[体积]] (即[[球 (数学)|球]]的体积)是 |
|||
其所包圍(封閉)的[[體積]]為: |
|||
: <math>V = \frac{4}{3}\pi r^3</math> |
|||
其中 {{mvar|r}} 是球面的半径。[[阿基米德]]首先推导出了这个公式,他通过证明球体内的体积是球体内部与外接[[圆柱体]](具有与球体直径相等的高度和直径)内部之间的体积差值的两倍而得出该公式。<ref>{{harvnb|Steinhaus|1969|loc=p. 223}}</ref> 这个说法可以根据[[祖暅原理]]得到。该公式也可以使用积分得出,即用截面积分(定积分)对无穷多的厚度无穷小的圆盘沿 {{mvar|x}} 轴从 {{math|1=''x'' = −''r''}} 到 {{math|1=''x'' = ''r''}} 堆积起来的体积求和,假设该球面半径为 {{mvar|r}},以原点为球心。 |
|||
在任何给定的 {{mvar|x}} 处,体积增量({{mvar|ΔV}})近似等于 {{mvar|x}} 处圆盘的面积与其厚度({{mvar|Δx}})的乘积: |
|||
:<math>V = \frac{4}{3}\pi r^3</math> |
|||
: <math>\Delta V \approx \pi y^2 \cdot \Delta x.</math> |
|||
当最厚的那一个圆盘厚度趋近0时,总体积是所有增量的总和: |
|||
球面的面積是包圍一定體積的表面中最小的,同樣的,以一定面積表面能包圍住的體積以球面為最大。也就是這個原因,在自然界中出現的氣泡或小水滴的形狀都接近球形,因為[[表面張力]]會使局部的表面積趨向最小。 |
|||
: <math>V = \lim_{ ||T|| \to 0 } \sum \pi y^2 \cdot \Delta x.</math> |
|||
其中 ||{{mvar|T}} || 表示当取分割 {{mvar|T}} 时,最厚的那个圆盘的厚度。此时体积为: |
|||
球面的外接[[圆柱体]]体积是球體体积的<math>\frac{3}{2}</math>,面积也是球面的<math>\frac{3}{2}</math>。 |
|||
: <math>V = \int_{-r}^{r} \pi y^2 \mathrm{d}x.</math> |
|||
在任何给定的 {{mvar|x}} 处,{{mvar|x}}、{{mvar|y}}、{{mvar|r}} 都可以构成一个直角三角形;因此,应用[[勾股定理]]得出: |
|||
== 參見 == |
|||
: <math>y^2 = r^2 - x^2.</math> |
|||
* [[球 (数学)]] |
|||
* [[類球面]] |
|||
将上式代入得到 |
|||
: <math>V = \int_{-r}^{r} \pi (r^2 - x^2) \mathrm{d}x,</math> |
|||
积分之后就可以得出结果 |
|||
: <math>V = \pi \left[r^2x - \frac{x^3}{3} \right]_{-r}^{r} = \pi \left(r^3 - \frac{r^3}{3} \right) - \pi \left(-r^3 + \frac{r^3}{3} \right) = \frac43\pi r^3.</math> |
|||
另外,此公式也可以用球坐标系计算,体积元可以写成 |
|||
: <math> \mathrm{d}V=\rho^2\sin\varphi\,\mathrm{d}\rho\,\mathrm{d}\theta\,\mathrm{d}\varphi</math> |
|||
因此得到[[三重积分]],并算出结果如下: |
|||
: <math>V=\int_0^{2\pi} \mathrm{d}\theta\,\int_{0}^{\pi} \mathrm{d}\varphi\,\int_0^r \rho^2\sin\theta \mathrm{d}\rho = \frac43\pi r^3.</math> |
|||
对于大多数实际用途而言,立方体的内接球的体积可以近似为立方体体积的52.4%,这是因为 {{math|1=''V'' = {{sfrac|{{pi}}|6}} ''d''<sup>3</sup>}},其中 {{mvar|d}} 是球面的直径,也是立方体的边长,{{sfrac|{{pi}}|6}} ≈ 0.5236。例如,直径1m的球的体积是边长为1m的立方体体积的52.4%,或约0.524 m<sup>3</sup>。 |
|||
==表面积== |
|||
半径为{{mvar|r}}的球体的[[表面積]]为: |
|||
:<math>A = 4\pi r^2.</math> |
|||
[[阿基米德]]首先根据“外接圆柱体侧面的投影是保持面积的”这个事实推导出这个公式<ref name="MathWorld_Sphere">{{cite mathworld|title=Sphere |id=Sphere}}</ref>。<ref>{{harvnb|Steinhaus|1969|loc=p. 221}}</ref> 另一种得到这个公式的方法基于如下事实,即球的表面积等于其体积公式关于 {{mvar|r}} 的[[导数]] ,因为半径为 {{mvar|r}} 的球体的体积可以认为是从半径0到半径 {{mvar|r}} 嵌套在一起的无穷小厚度的无穷多个同心球壳的表面积的总和。在无穷小的厚度下,任何给定球壳的内外表面面积是相等的,半径 {{mvar|r}} 处的体积元可以简单地认为是半径 {{mvar|r}} 处的表面积与无穷小厚度的乘积。 |
|||
在任何给定半径 {{mvar|r}} 处,<ref>{{mvar|r}}在这个计算中被认为是一个变量</ref> 体积增量({{mvar|ΔV}})等于半径 {{mvar|r}} 处表面积({{math|''A''(''r'')}})与球壳厚度({{mvar|Δr}})的乘积: |
|||
:<math>\Delta V \approx A(r) \cdot \Delta r. </math> |
|||
总体积是所有球壳体积的总和: |
|||
:<math>V \approx \sum A(r) \cdot \Delta r.</math> |
|||
该等式在最厚的那一个圆盘的 {{mvar|Δr}} 趋近于 0 时<ref name="delta">Pages 141, 149. {{cite book |
|||
|author1=E. J. Borowski |author2=J. M. Borwein |title=Collins Dictionary of Mathematics |
|||
|year=1989 |url=https://archive.org/details/dictionaryofmath0000boro |isbn=0-00-434347-6}}</ref>为: |
|||
:<math>V = \int_0^r A(r) \, \mathrm{d}r.</math> |
|||
代入 {{mvar|V}}: |
|||
:<math>\frac43\pi r^3 = \int_0^r A(r) \, \mathrm{d}r.</math> |
|||
将等式两边对 {{mvar|r}} 求导就会得到 {{mvar|A}} 关于 {{mvar|r}} 的函数: |
|||
:<math>4\pi r^2 = A(r).</math> |
|||
这通常写为: |
|||
:<math>A = 4\pi r^2,</math> |
|||
其中 {{mvar|r}} 是球面的半径。 |
|||
再来看一种方法,球面上的面积元可以用球坐标系给出:{{math|1=''dA'' = ''r''<sup>2</sup> sin ''φ dθ dφ''}}。用笛卡尔坐标来表示的话,面积元就会写成 |
|||
: <math>\mathrm{d}S=\frac{r}{\sqrt{r^{2}-{\displaystyle \sum_{i\ne k}x_{i}^{2}}}}\prod_{i\ne k}\mathrm{d}x_{i},\;\forall k.</math> |
|||
更一般性的表达,请参阅[[面积元]]条目。 |
|||
因此总面积可以通过[[积分]]得到: |
|||
:<math>A =\int_0^{2\pi}\mathrm{d}\theta\,\int_0^\pi r^2 \sin{\varphi}\mathrm{d}\varphi=\int_0^{2\pi}[-r^2\cos{\varphi}]_0^{\pi}\,\mathrm{d}\theta= 4\pi r^2.</math> |
|||
[[Image:Einstein gyro gravity probe b.jpg|thumb|上图中的球体被认为是最精确的人造球体之一,它[[折射]]出背景中[[爱因斯坦]]的画像。这个球体是[[引力探测器B]]实验中所用的{{link-en|熔融石英|Fused quartz}}[[陀螺仪]],它在形状上和完美球体之间的误差不超过40颗原子(不到10[[纳米]])厚度。2008年7月1日,一些来自[[澳大利亚]]的科学家宣称他们制造出了更加接近完美的球体,准确率为0.3纳米,它的创造背景是当年科学家们在寻求一[[千克]]的新标准。<ref>[https://www.newscientist.com/article/dn14229-roundest-objects-in-the-world-created.html New Scientist | Technology | Roundest objects in the world created] {{webarchive|url=https://web.archive.org/web/20150426212426/http://www.newscientist.com/article/dn14229-roundest-objects-in-the-world-created.html |date=2015-04-26 }}</ref>]] |
|||
球面是包围给定体积的所有曲面中面积最小的,球面还是给定表面积的所有闭合曲面中包围体积最大的。因此球面在自然界中出现:例如,气泡和小水滴大致为球形,因为[[表面張力係數|表面张力]]会局部最小化表面积。 |
|||
球的质量与表面积之比称为比表面积,可以由上述等式表示出来 |
|||
:<math>\mathrm{SSA} = \frac{A}{V\rho} = \frac{3}{r\rho},</math> |
|||
其中 {{mvar|ρ}} 为[[密度]](质量与体积之比)。 |
|||
==几何性质== |
|||
球面由四个不共面的点唯一确定。更一般地说,球面由四个条件唯一确定,例如通过一个点、与一个平面相切,等等。 <ref>{{harvnb|Albert|2016|loc=p. 55}}</ref> 该性质类似于三个非共线的点确定平面中的唯一圆的性质。 |
|||
因此,一个球体由一个圆和一个不在该圆平面内的点唯一确定。 |
|||
通过检查两个球面方程的共同解,可以看出两个球相交于一个圆,包含该圆的平面称作相交球的'''基本平面''' 。<ref>{{harvnb|Albert|2016|loc=p. 57}}</ref> 虽然基本平面是一个实平面,但这个圆可能是虚圆(两个球面没有实的公共点),也可能由单个点组成(两个球面在该点相切)。<ref name="Woods267">{{harvnb|Woods|1961|loc=p. 267}}</ref> |
|||
在实交点处的两个球面之间的夹角是由该点处的球体的切面确定的[[二面角]]。两个球面在相交圆的所有点处的夹角都是相同的。<ref>{{harvnb|Albert|2016|loc=p. 58}}</ref> 当且仅当它们的球心之间的距离的平方等于其半径的平方和时,它们的交角才是直角(相互[[正交]])。<ref name="Woods266"></ref> |
|||
===球面束=== |
|||
如果 {{math|1=''f''(''x'', ''y'', ''z'') = 0}} 和 {{math|1=''g''(''x'', ''y'', ''z'') = 0}} 是两个不同球面的方程,那么 |
|||
:<math>s f(x,y,z) + t g(x,y,z) = 0</math> |
|||
当参数 {{mvar|s}} 和 {{mvar|t}} 是任意值时,也是球面方程。满足该等式的所有球体的集合称为由原始两个球体确定的'''球面束'''。在这个定义中,允许球面是一个平面(无限半径,球心在无穷远处),而如果两个原始球面都是平面,那么束的所有球面都是平面,否则在球面束中只会有一个平面(基本平面)。<ref name="Woods266"></ref> |
|||
如果球面束不是由所有平面组成,那么有三种类型的束:<ref name="Woods267"></ref> |
|||
*若球面相交于一个实圆 {{mvar|C}},则球面束由包含 {{mvar|C}} 的所有球面(包括基本平面)组成。球面束中所有普通球面的中心位于穿过 {{mvar|C}} 的中心并垂直于基本平面的直线(下面称作“中心线”)上。 |
|||
*若球面相交于一个虚圆,球面束的所有球面也会通过这个虚圆,但是其实这些普通球面不相交(没有真正的公共点)。中心线垂直于这个基本平面,这是一个真实的平面,但其中包含了一个假想的圆。 |
|||
*如果球面相交于一点 {{mvar|A}},则所有在这个面内的球面 {{mvar|A}} 都是相切的,同时基本面是所有这些面的公切面。中心线在 {{mvar|A}} 处垂直于基本平面。 |
|||
所有从基本平面的固定点到球面束的一个球面的切线的长度都是相同的。 <ref name="Woods267"></ref> |
|||
基本平面是与球面束中所有球面正交的所有球面的中心的轨迹。而且,与球体束的任何两个球体正交的球体,与球面束的所有球面正交,并且其中心位于球面束的基本平面中。 <ref name="Woods267"></ref> |
|||
==术语== |
|||
穿过球心的一条直线与球面相交,这两个相对称的交点称为对径点。[[大圆]]是球面上的一个圆,与球面具有相同的中心和半径,大圆所在的平面能将球面分成两个相同的部分。球面的截面称为'''圆面截口'''(spheric sections)。圆面截口均为圆,除了大圆以外的其他圆称为'''小圆'''。 <ref>{{cite mathworld|id=SphericSection |title=Spheric section}}</ref> |
|||
球面上两个不同非对径点之间的最短距离是过这两个点的唯一大圆上的两个圆弧中劣弧的长度。有了这个“大圆距离”,大圆就成为了黎曼圆。 |
|||
若将球面上任意一点设为该球面的''北极'',与该点相对应的对径点则被称为''南极'',而[[赤道]]则是与这两个极点等距的大圆。 过这两个极点的大圆被称为[[经线|子午线]]或[[经度|经线]],过这两个极点的直线被称为旋转轴。而[[纬度]]则是球面上与赤道平行的圆。这个术语也同样适用于那些与[[地球]]表面一样近似于[[類球面|球面]]的天体 (见[[大地水准面]])。 |
|||
==半球面== |
|||
{{anchor|hemisphere}} |
|||
任何过球心的平面都把它分成两个相等的半球面。过球心的任何两个相交平面都将球体细分为四个球面二角形,其顶点全部与位于平面交线上的对径点重合。 |
|||
球体的对径商空间是[[实射影平面]],它也可以被看作是北半球,赤道的对映点被确定。 |
|||
有猜想认为半球是黎曼圆的最佳(最小面积)等长填充。 |
|||
==推广== |
|||
===维数=== |
|||
{{Main|n维球面}} |
|||
球面可以推广到任意维数的[[維度|空间]]。对于任意[[自然数]]{{mvar|n}},{{mvar|n}}-球面(常写为{{math|''S''<sup>''n''</sup>}})是({{math|''n'' + 1}})维欧几里得空间中离该空间的一个中心点距离固定为{{mvar|r}}的点的集合,其中{{mvar|r}}与前面一样是正实数。特别地: |
|||
*{{math|''S''<sup>0</sup>}}:0-球体是实线的区间{{math|[−''r'', ''r'']}}的一对端点 |
|||
*{{math|''S''<sup>1</sup>}}:1-球面是半径为''r'' 的[[圆]] |
|||
*{{math|''S''<sup>2</sup>}}:2-球面是普通的球面 |
|||
*{{math|''S''<sup>3</sup>}}:[[三維球面|3-球面]]是四维欧氏空间中的球面。 |
|||
{{math|''n'' > 2}}的球面有时称作超球面 。 |
|||
以原点为中心的单位半径{{mvar|n}}球面表示为{{math|''S''<sup>''n''</sup>}},通常称为“{{mvar|n}}球面”。请注意,普通球面是一个2-球面,因为它是一个二维曲面(它嵌入在三维空间中)。 |
|||
单位({{math|''n''-1}})-球面的表面积是 |
|||
:<math>\frac{2 \pi^{\frac{n}{2}}}{\Gamma\left(\frac{n}{2}\right)}</math> |
|||
其中{{math|Γ(''z'')}}是欧拉[[Γ函数|发现的伽马函数]] 。 |
|||
表面积的另一种表达式为 |
|||
:<math> \begin{cases} |
|||
\displaystyle \frac{(2\pi)^{n/2}\,r^{n-1}}{2 \cdot 4 \cdots (n-2)}, & \text{if } n \text{ is even}; \\ \\ |
|||
\displaystyle \frac{2(2\pi)^{(n-1)/2}\,r^{n-1}}{1 \cdot 3 \cdots (n-2)}, & \text{if } n \text{ is odd}. |
|||
\end{cases}</math> |
|||
体积等于表面积乘以{{math|{{sfrac|''r''|''n''}}}},或者说 |
|||
:<math> \begin{cases} |
|||
\displaystyle \frac{(2\pi)^{n/2}\,r^n}{2 \cdot 4 \cdots n}, & \text{if } n \text{ is even}; \\ \\ |
|||
\displaystyle \frac{2(2\pi)^{(n-1)/2}\,r^n}{1 \cdot 3 \cdots n}, & \text{if } n \text{ is odd}. |
|||
\end{cases}</math> |
|||
对于{{mvar|n}}球的体积也存在一般递归公式。 |
|||
===度量空间=== |
|||
更一般地,在[[度量空间]] {{math|(''E'',''d'')}} 中,中心{{mvar|x}}、半径{{math|''r'' > 0}}的球面是使得{{math|1=''d''(''x'',''y'') = ''r''}}的点{{mvar|y}}的集合。 |
|||
如果球心是位于{{mvar|E}}的原点(如在[[范数|赋范]]空间中那样)的话,定义和符号中没有提及它。如果等于1,则半径也是如此,例如[[单位球面|单位球体]]的情况。 |
|||
与[[球 (数学)|球体]]不同的是,即使是一个大球面也可能是一个空集。例如,在欧几里德度量 {{math|'''Z'''<sup>''n''</sup>}} 中,只有{{math|''r''<sup>2</sup>}}可以写成[[整数]]的{{math|''n''}}平方和时,半径{{math|''r''}}的球面才是非空的。 |
|||
==拓扑学== |
|||
在[[拓扑学]]中,{{mvar|n}}球面定义为与{{math|(''n'' + 1)}}球体的边界同胚的空间;因此它与欧几里德{{mvar|n}}球体同胚 ,但可能缺少其[[度量空间|度量]] 。 |
|||
*0-球面是一对具有离散拓扑的点。 |
|||
*1-球面是一个圆([[同胚]]意义下)。因此,例如(任何扭结的像)是1-球面。 |
|||
*2-球面就是普通的球面([[同胚]]意义下)。因此,例如,任何[[類球面|类球面]]都是2-球面。 |
|||
{{mvar|n}}球面记为{{math|''S<sup>n</sup>''}} 。它是没有[[边界 (拓扑学)|边界]]的[[紧空间|紧致]][[拓扑流形|拓扑流形的]]一个例子。球面不必是光滑的;如果它是光滑的,它就不需要与欧几里得球面微分同胚 。 |
|||
[[海涅-博雷尔定理]]表明欧几里德{{mvar|n}}球面是紧致的。球面是连续函数{{math|{{norm|''x''}}}}下单点集的逆象。因此,球面是闭合的。{{math|''S<sup>n</sup>''}}也是有界的;所以它是紧致的。 |
|||
值得注意的是,在[[三維空間|三维空间]]中是可以把普通的球面内外翻转过来的,这个过程称作球面外翻,过程中可能会发生自交,但不会产生任何折痕。 |
|||
==球面几何== |
|||
[[File:Sphere halve.png|thumb|right|球面上的大圆]] |
|||
{{Main|球面幾何學}} |
|||
欧几里得平面几何的基本要素是[[点]]和线。在球面上,点以通常的意义来定义。“线”的类似物是[[测地线]],测地线是一个[[大圆|大圈]];大圆的界定性特征是含有其所有点的平面也穿过球心。[[弧长]]测量表明,球面上两点之间的最短路径是过这两点的[[大圆]]的较短的那一段圆弧。 |
|||
经典几何的许多定理也适用于球面几何,但并非所有的定理都是这样,因为球面不能满足一些经典几何的假设,包括[[平行公設|平行假设]]。在[[球面三角學|球面三角学]]中,[[角]]是在大圆之间定义的。球面三角学在许多方面与普通的[[三角学]]不同。例如,球形三角形的内角之和总是超过180度。而且,任何两个相似的球面三角形都是全等的。 |
|||
==球面的十一种性质== |
|||
[[File:Sphere section.png|thumb|球面的一个法向量,一个法平面及其正截面。交叉曲线的曲率是截面曲率。对于球面,通过给定点的每个法线段将是一个半径相同的圆(半径为球的半径)。这意味着球面上的每个点都是脐点。]] |
|||
在[[大卫·希尔伯特|David Hilbert]]和Stephan Cohn-Vossen的著作《几何与想象》 <ref>{{cite book |
|||
|author=[[David Hilbert|Hilbert, David]]; Cohn-Vossen, Stephan |
|||
|title=Geometry and the Imagination |
|||
|edition=2nd |
|||
|year=1952 |
|||
|publisher=Chelsea |
|||
|isbn=0-8284-1087-9}}</ref>一书中,统一描述了球面的11种性质,并讨论了这些性质是否仅仅存在于确定球面之中。一些性质对于平面来说也是成立的,因为平面可以视作半径无限大的球面。这些性质为: |
|||
#''球面上任意点与球心的距离都是相同的。同时,它和某两个固定点之间的距离之比是恒定的。'' |
|||
#:第一句一般是球面的定义,可以唯一确定球面。而第二句的结论与[[阿波罗尼斯圆]]类似,很容易被推导出,第二句的结论也适用于平面。 |
|||
#''球面的外轮廓和用平面截出的截面都是圆。'' |
|||
#:该性质是球面独有的性质。 |
|||
#''球面的径长和周长保持不变。'' |
|||
#:曲面的径长是指两个与该曲面相切的互相平行的平面的距离。除了球面之外,还有很多的闭合凸面的径长也是恒定不变的,例如迈斯纳结构 。而曲面的[[周长]]是在平面上的正交投影的边界长度。从这两者中任意性质出发都可以推出另一个性质。 |
|||
#''球面的所有点都是脐点 。'' |
|||
#:因为球面上的法线是由球心向外辐射的,所以在球面上任意一点的 法线与其外表面的夹角都成直角。过法线的平面与曲面的交线形成的曲线称为''法曲线'',法曲线的曲率为也被称为''法曲率''。对于大多数曲面上大部分的点,不同的法曲线的法曲率也不同;而这些法曲率的最大值和最小值被称为[[主曲率]] 。任何闭合的曲面上至少有四个''脐点''。脐点上所有的法曲率是相等的;包括其[[主曲率]]也是相等的。脐点可以被认为是曲面上最像球面的点。 |
|||
#:球面上所有法曲线的曲率都是相等的,所以每个点都是脐点。曲面中,只有球面和平面具有此性质。 |
|||
#''球体是没有中心表面的。'' |
|||
#:对于一个给定的法曲线,存在一个曲率等于截面曲率的曲率圆与曲面相切,圆心位于其法线上。例如,对应其最大和最小截面曲率的两个圆心被称为''焦点'' ,所有这些圆心的集合形成的面叫做焦面 。 |
|||
#:对于大多数曲面来说,焦面会形成两个曲面在脐点处相交。一下几种特殊的情况: |
|||
#:*对于管道曲面,一层焦面形成曲线,另一层焦面形成为曲面 |
|||
#:*对于[[圆锥|圆锥体]] ,圆柱体, [[环面]]和环形曲线两层焦面都形成曲面。 |
|||
#:*在球面上,每一个大圆的圆心都在球体的球心,而焦面形成一个点该性质是球面独有的。 |
|||
#''球面上的所有测地线都是闭合曲线。'' |
|||
#:测地线是球面表面上的曲线,也是两点之间的最短距离。它们是平面几何中直线概念的一种概括性表达。对于球面来说,测地线是一个大的圆。许多其他的曲面都有这种性质。 |
|||
#''在体积大小一定的情况下,球面的表面积最小;而在表面积的大小固定的情况下,球面则能包围最大的体积。'' |
|||
#:这个性质源自自等[[等周定理|周不等式]] 。这些性质唯一地定义了球面,例如在[[肥皂泡]]中:肥皂泡包围的体积不变, 其[[表面張力係數|表面张力]]使得其表面积最小。一个自由浮动的肥皂泡因此近似于一个球体(尽管由于重力这样的外力会轻微使得肥皂泡的形状变得扭曲)。 |
|||
#''在所有已经给定表面积的凸固体中,球面的总平均曲率是最小的。'' |
|||
#:[[平均曲率]]是两个主曲率的平均值,这是恒定的一个数值,因为球面上的所有点的主曲率都是相等的。 |
|||
#''球面的平均曲率是恒定的。'' |
|||
#:球面是唯一没有边界和奇异点而有恒定正平均曲率的嵌入面。其他如最小曲面这样的沉浸面的平均曲率也是恒定的。 |
|||
#''球面的高斯曲率是一个常数。'' |
|||
#:[[高斯曲率]]是两个主曲率的乘积。它是一种可以通过测量长度和角度来确定的固有性质,与曲面如何嵌入这个空间无关。因此,折弯曲面并不会改变高斯曲率,而其他高斯曲率不变的曲面则可以通过在球面上切割一个小狭缝并折弯来得到。所有其他的曲面都有边界,球面是唯一没有边界的曲面,因为它的高斯曲率是一个常数。[[伪球面]]是一个高斯曲率为负且不变的曲面的例子。 |
|||
#''球面是由一个由三参数所组成的刚性运动所构成的。'' |
|||
#:围绕任何轴旋转,在原点处的单位球会将球面阴影映射到其自身上。任何绕着过原点的直线的旋转都可以表示为在三坐标轴上旋转的组合 |
|||
(详见[[欧拉角]])。因此,存在一个三参数的旋转族,使得每次旋转将球面转换成自身;这个族被称为旋转组SO(3)。该平面是唯一具有三参数变换族的一个曲面(沿原点周围的{{mvar|x}}{{mvar|y}}轴旋转和平移)。圆柱体是唯一具有双参数系列刚性运动的表面,并且[[旋轉曲面|旋转表面]]和螺旋面是具有单参数系列的表面。 |
|||
==参见== |
|||
[[File:King of spades- spheres.jpg|thumb|演示工程仪器的扑克牌,英格兰,1702。黑桃K:球体]] |
|||
{{div col||colwidth=20em}} |
|||
*[[三維球面]] |
|||
*{{le|仿射球面|Affine sphere}} |
|||
*{{le|亚历山大带角球|Alexander horned sphere}} |
|||
*{{le|天球图|Celestial spheres}} |
|||
*[[立方體]] |
|||
*[[曲率]] |
|||
*{{le|方向统计|Directional statistics}} |
|||
*[[球冠]] |
|||
*[[戴森球]] |
|||
*{{le|手与反射的球|Hand with Reflecting Sphere}},[[莫里茲·柯尼利斯·艾雪|M·C·艾雪]]自画像绘图说明镜面球体的反射和光学性质 |
|||
*{{le|霍伯曼球面|Hoberman sphere}} |
|||
*[[同調球面]] |
|||
*{{le|球面的同伦群|Homotopy groups of spheres}} |
|||
*{{le|同伦球面|Homotopy sphere}} |
|||
*[[超球面]] |
|||
*{{le|Lenart球面|Lenart Sphere}} |
|||
*{{le|餐巾环问题|Napkin ring problem}} |
|||
*[[Orb (optics)]] |
|||
*{{le|伪球面|Pseudosphere}} |
|||
*[[黎曼球面]] |
|||
*[[立體角]] |
|||
*[[最密堆积]] |
|||
*[[球座標系]] |
|||
*[[地圆说]] |
|||
*球面螺旋线,恒定进动曲线的{{le|切线标线|tangent indicatrix}} |
|||
*{{le|球心角体|Spherical sector}} |
|||
*{{le|球截形|Spherical segment}} |
|||
*{{le|球壳|Spherical shell}} |
|||
*{{le|球面楔|Spherical wedge}} |
|||
*[[球台]] |
|||
*[[措爾曲面]] |
|||
{{div col end}} |
|||
==注释== |
|||
{{reflist}} |
|||
==参考文献== |
|||
{{Wikisource1911Enc|Sphere}} |
|||
*{{citation|first=Abraham Adrian|last=Albert|title=Solid Analytic Geometry|year=2016|origyear=1949|publisher=Dover|isbn=978-0-486-81026-3}} |
|||
*{{cite book|first=William |last=Dunham |pages=28, 226 |title=The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities |isbn=0-471-17661-3 }} |
|||
* {{ citation | first1 = Erwin | last1 = Kreyszig | year = 1972 | isbn = 0-471-50728-8 | title = Advanced Engineering Mathematics | edition = 3rd | publisher = [[John Wiley & Sons|Wiley]] | location = New York }} |
|||
*{{citation|first=H.|last=Steinhaus|title=Mathematical Snapshots|year=1969|publisher=Oxford University Press|edition=Third American}} |
|||
*{{citation|first=Frederick S.|last=Woods|title=Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry|year=1961|origyear=1922|publisher=Dover}} |
|||
==外部链接== |
|||
{{Sister project links}} |
|||
*[[planetmath:186|球体(PlanetMath.org)]] |
|||
*{{MathWorld |id=Sphere |title=Sphere}} |
|||
*[[Wikibooks:Mathematica/Uniform Spherical Distribution|Mathematica/均匀球形分布]] |
|||
*[http://mathschallenge.net/index.php?section=faq&ref=geometry/surface_sphere 球表面积] {{Wayback|url=http://mathschallenge.net/index.php?section=faq&ref=geometry%2Fsurface_sphere |date=20200925201137 }} |
|||
{{Authority control}} |
{{Authority control}} |
||
[[Category:初等几何|Q]] |
|||
[[Category: |
[[Category:微分几何]] |
||
[[Category: |
[[Category:微分拓扑学]] |
||
[[Category: |
[[Category:初等几何]] |
||
[[Category: |
[[Category:基本的形状]] |
||
[[Category:均匀的空间]] |
|||
[[Category:球]] |
|||
[[Category:曲面]] |
[[Category:曲面]] |
||
[[Category:拓扑学]] |
|||
2022年11月23日 (三) 03:05的最新版本
| 几何学 |
|---|
 |
| 几何学家 |
|
|
球面 (英語:sphere)是三维空间中完全圆形的几何物体,它是圆球的表面(类似于在二维空间中,“圆 ”包围着“圆盘”那样)。
就像在二维空间中的圆的定义一样,球面在数学上定义为三维空间中离给定的点距离相同的点的集合 r。 [1] 这个距离 r 是球的半径 ,球(ball)则是由离给定点距离小于 r 的所有点构成的几何体,而这个给定点就是球心。球的半径和球心也是球面的半径和中心。两端都在球面上的最长线段通过球心,其长度是其半径的两倍;它是球面和球体的直径 。
尽管在数学之外,术语“球面”和“球”有时可互换使用,但在数学中是明确区分的:球面是一种嵌在三维欧几里得空间内的二维封闭曲面,而球是一种三维图形,其包括球面和球面内部的一切(闭球),不过更常见的定义是只包括球面内部的所有点,不包括球面上的点(开球)。这种区别并不总是保持不变,尤其是在旧的数学文献里,sphere(球面)被当作固体。这与在平面上混用术语“圆”(circle)和“圆盘”(disk)的情况类似。
三维空间中的方程
[编辑]在解析几何中,球心为 (x0, y0, z0),半径为 r 的球面是满足下面方程的所有点 (x, y, z) 的轨迹
令 a, b, c, d, e 为实数,a ≠ 0,并且
如果 ,则那么下面的方程
没有实数根,称为虚球面的方程。如果 ,则 的唯一解是点 ,此时该方程称作点球面的方程。还有一种,就是在 的情况下, 是球面的方程,其中心是,半径是。[1]
如果上述等式中的 a 是零,那么 f(x, y, z) = 0 就成为了平面方程。因此,平面可以认为是球心在无穷远点的球面。[2]
半径 ,中心在 的球面上的点可以写成参数方程
以原点为中心的任意半径的球面是以下微分形式的积分曲面:
这个方程反映了在球面上行进的点的位置 (x, y, z) 和速度向量 (dx, dy, dz) 总是彼此正交的。
球面还可以通过以任何直径为轴,把圆旋转一周形成的表面来构造。由于圆是一种特殊的椭圆 ,所以球面也是一种特殊的椭球面。椭圆围绕其长轴旋转形成的曲面,就是长球面;如果绕短轴旋转,就会形成一个扁球面。[4]
包围的体积
[编辑]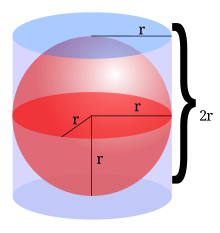
其中 r 是球面的半径。阿基米德首先推导出了这个公式,他通过证明球体内的体积是球体内部与外接圆柱体(具有与球体直径相等的高度和直径)内部之间的体积差值的两倍而得出该公式。[5] 这个说法可以根据祖暅原理得到。该公式也可以使用积分得出,即用截面积分(定积分)对无穷多的厚度无穷小的圆盘沿 x 轴从 x = −r 到 x = r 堆积起来的体积求和,假设该球面半径为 r,以原点为球心。
在任何给定的 x 处,体积增量(ΔV)近似等于 x 处圆盘的面积与其厚度(Δx)的乘积:
当最厚的那一个圆盘厚度趋近0时,总体积是所有增量的总和:
其中 ||T || 表示当取分割 T 时,最厚的那个圆盘的厚度。此时体积为:
在任何给定的 x 处,x、y、r 都可以构成一个直角三角形;因此,应用勾股定理得出:
将上式代入得到
积分之后就可以得出结果
另外,此公式也可以用球坐标系计算,体积元可以写成
因此得到三重积分,并算出结果如下:
对于大多数实际用途而言,立方体的内接球的体积可以近似为立方体体积的52.4%,这是因为 V = π/6 d3,其中 d 是球面的直径,也是立方体的边长,π/6 ≈ 0.5236。例如,直径1m的球的体积是边长为1m的立方体体积的52.4%,或约0.524 m3。
表面积
[编辑]半径为r的球体的表面積为:
阿基米德首先根据“外接圆柱体侧面的投影是保持面积的”这个事实推导出这个公式[6]。[7] 另一种得到这个公式的方法基于如下事实,即球的表面积等于其体积公式关于 r 的导数 ,因为半径为 r 的球体的体积可以认为是从半径0到半径 r 嵌套在一起的无穷小厚度的无穷多个同心球壳的表面积的总和。在无穷小的厚度下,任何给定球壳的内外表面面积是相等的,半径 r 处的体积元可以简单地认为是半径 r 处的表面积与无穷小厚度的乘积。
在任何给定半径 r 处,[8] 体积增量(ΔV)等于半径 r 处表面积(A(r))与球壳厚度(Δr)的乘积:
总体积是所有球壳体积的总和:
该等式在最厚的那一个圆盘的 Δr 趋近于 0 时[9]为:
代入 V:
将等式两边对 r 求导就会得到 A 关于 r 的函数:
这通常写为:
其中 r 是球面的半径。
再来看一种方法,球面上的面积元可以用球坐标系给出:dA = r2 sin φ dθ dφ。用笛卡尔坐标来表示的话,面积元就会写成
更一般性的表达,请参阅面积元条目。
因此总面积可以通过积分得到:

球面是包围给定体积的所有曲面中面积最小的,球面还是给定表面积的所有闭合曲面中包围体积最大的。因此球面在自然界中出现:例如,气泡和小水滴大致为球形,因为表面张力会局部最小化表面积。
球的质量与表面积之比称为比表面积,可以由上述等式表示出来
其中 ρ 为密度(质量与体积之比)。
几何性质
[编辑]球面由四个不共面的点唯一确定。更一般地说,球面由四个条件唯一确定,例如通过一个点、与一个平面相切,等等。 [11] 该性质类似于三个非共线的点确定平面中的唯一圆的性质。
因此,一个球体由一个圆和一个不在该圆平面内的点唯一确定。
通过检查两个球面方程的共同解,可以看出两个球相交于一个圆,包含该圆的平面称作相交球的基本平面 。[12] 虽然基本平面是一个实平面,但这个圆可能是虚圆(两个球面没有实的公共点),也可能由单个点组成(两个球面在该点相切)。[13]
在实交点处的两个球面之间的夹角是由该点处的球体的切面确定的二面角。两个球面在相交圆的所有点处的夹角都是相同的。[14] 当且仅当它们的球心之间的距离的平方等于其半径的平方和时,它们的交角才是直角(相互正交)。[2]
球面束
[编辑]如果 f(x, y, z) = 0 和 g(x, y, z) = 0 是两个不同球面的方程,那么
当参数 s 和 t 是任意值时,也是球面方程。满足该等式的所有球体的集合称为由原始两个球体确定的球面束。在这个定义中,允许球面是一个平面(无限半径,球心在无穷远处),而如果两个原始球面都是平面,那么束的所有球面都是平面,否则在球面束中只会有一个平面(基本平面)。[2]
如果球面束不是由所有平面组成,那么有三种类型的束:[13]
- 若球面相交于一个实圆 C,则球面束由包含 C 的所有球面(包括基本平面)组成。球面束中所有普通球面的中心位于穿过 C 的中心并垂直于基本平面的直线(下面称作“中心线”)上。
- 若球面相交于一个虚圆,球面束的所有球面也会通过这个虚圆,但是其实这些普通球面不相交(没有真正的公共点)。中心线垂直于这个基本平面,这是一个真实的平面,但其中包含了一个假想的圆。
- 如果球面相交于一点 A,则所有在这个面内的球面 A 都是相切的,同时基本面是所有这些面的公切面。中心线在 A 处垂直于基本平面。
所有从基本平面的固定点到球面束的一个球面的切线的长度都是相同的。 [13]
基本平面是与球面束中所有球面正交的所有球面的中心的轨迹。而且,与球体束的任何两个球体正交的球体,与球面束的所有球面正交,并且其中心位于球面束的基本平面中。 [13]
术语
[编辑]穿过球心的一条直线与球面相交,这两个相对称的交点称为对径点。大圆是球面上的一个圆,与球面具有相同的中心和半径,大圆所在的平面能将球面分成两个相同的部分。球面的截面称为圆面截口(spheric sections)。圆面截口均为圆,除了大圆以外的其他圆称为小圆。 [15]
球面上两个不同非对径点之间的最短距离是过这两个点的唯一大圆上的两个圆弧中劣弧的长度。有了这个“大圆距离”,大圆就成为了黎曼圆。
若将球面上任意一点设为该球面的北极,与该点相对应的对径点则被称为南极,而赤道则是与这两个极点等距的大圆。 过这两个极点的大圆被称为子午线或经线,过这两个极点的直线被称为旋转轴。而纬度则是球面上与赤道平行的圆。这个术语也同样适用于那些与地球表面一样近似于球面的天体 (见大地水准面)。
半球面
[编辑]任何过球心的平面都把它分成两个相等的半球面。过球心的任何两个相交平面都将球体细分为四个球面二角形,其顶点全部与位于平面交线上的对径点重合。
球体的对径商空间是实射影平面,它也可以被看作是北半球,赤道的对映点被确定。
有猜想认为半球是黎曼圆的最佳(最小面积)等长填充。
推广
[编辑]维数
[编辑]球面可以推广到任意维数的空间。对于任意自然数n,n-球面(常写为Sn)是(n + 1)维欧几里得空间中离该空间的一个中心点距离固定为r的点的集合,其中r与前面一样是正实数。特别地:
n > 2的球面有时称作超球面 。
以原点为中心的单位半径n球面表示为Sn,通常称为“n球面”。请注意,普通球面是一个2-球面,因为它是一个二维曲面(它嵌入在三维空间中)。
单位(n-1)-球面的表面积是
其中Γ(z)是欧拉发现的伽马函数 。
表面积的另一种表达式为
体积等于表面积乘以r/n,或者说
对于n球的体积也存在一般递归公式。
度量空间
[编辑]更一般地,在度量空间 (E,d) 中,中心x、半径r > 0的球面是使得d(x,y) = r的点y的集合。
如果球心是位于E的原点(如在赋范空间中那样)的话,定义和符号中没有提及它。如果等于1,则半径也是如此,例如单位球体的情况。
与球体不同的是,即使是一个大球面也可能是一个空集。例如,在欧几里德度量 Zn 中,只有r2可以写成整数的n平方和时,半径r的球面才是非空的。
拓扑学
[编辑]在拓扑学中,n球面定义为与(n + 1)球体的边界同胚的空间;因此它与欧几里德n球体同胚 ,但可能缺少其度量 。
n球面记为Sn 。它是没有边界的紧致拓扑流形的一个例子。球面不必是光滑的;如果它是光滑的,它就不需要与欧几里得球面微分同胚 。
海涅-博雷尔定理表明欧几里德n球面是紧致的。球面是连续函数||x||下单点集的逆象。因此,球面是闭合的。Sn也是有界的;所以它是紧致的。
值得注意的是,在三维空间中是可以把普通的球面内外翻转过来的,这个过程称作球面外翻,过程中可能会发生自交,但不会产生任何折痕。
球面几何
[编辑]
欧几里得平面几何的基本要素是点和线。在球面上,点以通常的意义来定义。“线”的类似物是测地线,测地线是一个大圈;大圆的界定性特征是含有其所有点的平面也穿过球心。弧长测量表明,球面上两点之间的最短路径是过这两点的大圆的较短的那一段圆弧。
经典几何的许多定理也适用于球面几何,但并非所有的定理都是这样,因为球面不能满足一些经典几何的假设,包括平行假设。在球面三角学中,角是在大圆之间定义的。球面三角学在许多方面与普通的三角学不同。例如,球形三角形的内角之和总是超过180度。而且,任何两个相似的球面三角形都是全等的。
球面的十一种性质
[编辑]
在David Hilbert和Stephan Cohn-Vossen的著作《几何与想象》 [16]一书中,统一描述了球面的11种性质,并讨论了这些性质是否仅仅存在于确定球面之中。一些性质对于平面来说也是成立的,因为平面可以视作半径无限大的球面。这些性质为:
- 球面上任意点与球心的距离都是相同的。同时,它和某两个固定点之间的距离之比是恒定的。
- 第一句一般是球面的定义,可以唯一确定球面。而第二句的结论与阿波罗尼斯圆类似,很容易被推导出,第二句的结论也适用于平面。
- 球面的外轮廓和用平面截出的截面都是圆。
- 该性质是球面独有的性质。
- 球面的径长和周长保持不变。
- 曲面的径长是指两个与该曲面相切的互相平行的平面的距离。除了球面之外,还有很多的闭合凸面的径长也是恒定不变的,例如迈斯纳结构 。而曲面的周长是在平面上的正交投影的边界长度。从这两者中任意性质出发都可以推出另一个性质。
- 球面的所有点都是脐点 。
- 球体是没有中心表面的。
- 球面上的所有测地线都是闭合曲线。
- 测地线是球面表面上的曲线,也是两点之间的最短距离。它们是平面几何中直线概念的一种概括性表达。对于球面来说,测地线是一个大的圆。许多其他的曲面都有这种性质。
- 在体积大小一定的情况下,球面的表面积最小;而在表面积的大小固定的情况下,球面则能包围最大的体积。
- 在所有已经给定表面积的凸固体中,球面的总平均曲率是最小的。
- 平均曲率是两个主曲率的平均值,这是恒定的一个数值,因为球面上的所有点的主曲率都是相等的。
- 球面的平均曲率是恒定的。
- 球面是唯一没有边界和奇异点而有恒定正平均曲率的嵌入面。其他如最小曲面这样的沉浸面的平均曲率也是恒定的。
- 球面的高斯曲率是一个常数。
- 球面是由一个由三参数所组成的刚性运动所构成的。
- 围绕任何轴旋转,在原点处的单位球会将球面阴影映射到其自身上。任何绕着过原点的直线的旋转都可以表示为在三坐标轴上旋转的组合
(详见欧拉角)。因此,存在一个三参数的旋转族,使得每次旋转将球面转换成自身;这个族被称为旋转组SO(3)。该平面是唯一具有三参数变换族的一个曲面(沿原点周围的xy轴旋转和平移)。圆柱体是唯一具有双参数系列刚性运动的表面,并且旋转表面和螺旋面是具有单参数系列的表面。
参见
[编辑]
注释
[编辑]- ^ 1.0 1.1 Albert 2016,p. 54
- ^ 2.0 2.1 2.2 Woods 1961,p. 266
- ^ Kreyszig (1972,第342頁)
- ^ Albert 2016,p. 60
- ^ Steinhaus 1969,p. 223
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Steinhaus 1969,p. 221
- ^ r在这个计算中被认为是一个变量
- ^ Pages 141, 149. E. J. Borowski; J. M. Borwein. Collins Dictionary of Mathematics. 1989. ISBN 0-00-434347-6.
- ^ New Scientist | Technology | Roundest objects in the world created 互联网档案馆的存檔,存档日期2015-04-26.
- ^ Albert 2016,p. 55
- ^ Albert 2016,p. 57
- ^ 13.0 13.1 13.2 13.3 Woods 1961,p. 267
- ^ Albert 2016,p. 58
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Hilbert, David; Cohn-Vossen, Stephan. Geometry and the Imagination 2nd. Chelsea. 1952. ISBN 0-8284-1087-9.
参考文献
[编辑]- Albert, Abraham Adrian, Solid Analytic Geometry, Dover, 2016 [1949], ISBN 978-0-486-81026-3
- Dunham, William. The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities. : 28, 226. ISBN 0-471-17661-3.
- Kreyszig, Erwin, Advanced Engineering Mathematics 3rd, New York: Wiley, 1972, ISBN 0-471-50728-8
- Steinhaus, H., Mathematical Snapshots Third American, Oxford University Press, 1969
- Woods, Frederick S., Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry, Dover, 1961 [1922]





















![{\displaystyle V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\right)={\frac {4}{3}}\pi r^{3}.}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/4c081de9760153a5ab7e59be1b9de1aa97d08dec)










![{\displaystyle A=\int _{0}^{2\pi }\mathrm {d} \theta \,\int _{0}^{\pi }r^{2}\sin {\varphi }\mathrm {d} \varphi =\int _{0}^{2\pi }[-r^{2}\cos {\varphi }]_{0}^{\pi }\,\mathrm {d} \theta =4\pi r^{2}.}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/b4a27c8ea81d50d501df7fb3bb0bff593f198ad3)




