双射:修订间差异
外观
删除的内容 添加的内容
小无编辑摘要 |
Add 1 book for verifiability (20240107)) #IABot (v2.0.9.5) (GreenC bot |
||
| (未显示40个用户的61个中间版本) | |||
| 第1行: | 第1行: | ||
{{No footnotes|time=2022-04-22T20:29:13+00:00}} |
|||
'''双射''',也称之为'''双射函数'''或者'''一一对应''',在[[数学]]中为一个既是[[单射]]也是[[满射]]的[[函数]],因此也称之为“'''一一对应到'''”。直观地说,一个双射函数形成一个对应,并且每一个输入值都有正好一个输出值以及每一个输出值都有正好一个输入值。 (在一些参考书中,“一一”用来指'''双射''',但是这里不用这个较老的用法。) |
|||
{{NoteTA |
|||
|G1 = Math |
|||
}} |
|||
[[File:Bijection.svg|thumb|200px|一个双射函数]] |
|||
{{各種函數}} |
|||
更加形式地,一个函数<math>f:X\rightarrow Y</math>为一个双射,[[当且仅当]][[陪域]]<math>Y</math>中的每一个<math>y</math>都有''正好一个''[[定义域]]<math>X</math>中的<math>x</math>满足<math>f(x)=y</math>。 |
|||
[[數學]]中,一個由[[集合 (数学)|集合]]<math>X</math>[[映射]]至集合<math>Y</math>的[[函數]],若對每一在<math>Y</math>內的<math>y</math>,存在唯一一個在<math>X</math>內的<math>x</math>与其对应,且對每一在<math>X</math>內的<math>x</math>,存在唯一一個在<math>Y</math>內的<math>y</math>与其对应,則此函數為'''對射函數'''。 |
|||
<table border="1"> |
|||
<tr><td align="center"> |
|||
[[Image:bijMap.png]]<br> |
|||
雙射(單射與滿射)</td> |
|||
<td align="center"> |
|||
[[Image:Mathmap.png]]<br> |
|||
單射但非滿射</td></tr> |
|||
<tr><td align="center"> |
|||
[[Image:ontoMap.png]]<br> |
|||
滿射但非單射</td> |
|||
<td align="center"> |
|||
[[Image:mathmap2.png]]<br> |
|||
非滿射非單射</td></tr> |
|||
</table> |
|||
換句話說,如果其為兩集合間的'''一一對應''',则<math>f</math>是雙射的。即,同時為[[單射]]和[[滿射]]。 |
|||
如果<math>X,Y</math>皆为[[实数]]<math>\mathbb{R}</math>,则双射函数<math>f:\mathbb{R}\rightarrow \mathbb{R}</math>可以被视觉化为两根任意的水平直线只相交正好一次。(这是水平线测试的一个特例。) |
|||
例如,由[[整數]]集合<math>\Z</math>至<math>\Z</math>的函數<math>\operatorname{succ}</math>,其將每一個整數<math>x</math>連結至整數<math>\operatorname{succ}(x)=x+1</math>,這是一個雙射函數;再看一個例子,函數<math>\operatorname{sumdif}</math>,其將每一對實數<math>(x,y)</math>連結至<math>\operatorname{sumdif}(x,y) = (x + y, x - y)</math>,這也是個雙射函數。 |
|||
如果<math>X,Y</math>皆为[[有限]][[集合]],则这两个集合中<math>X,Y</math>之间存在一个双射,[[当且仅当]]X和Y的[[元素]]数相等。其实,在[[公理集合论]]中,''元素数相同''的定义被认为是个特例,一般化这个定义到[[无限集合]]需要导入[[基数]]的概念,这是一个区别各类不同大小的[[无限集合]]的方法。 |
|||
一雙射函數亦簡稱為'''雙射'''({{lang-en|bijection}})或'''[[置換]]'''。後者一般較常使用在<math>X=Y</math>時。以由<math>X</math>至<math>Y</math>的所有雙射組成的集合標記為<math>X \leftrightarrow Y </math>。 |
|||
== 例子和反例 == |
|||
雙射函數在許多數學領域扮演著很基本的角色,如在[[同構]]的定義(以及如[[同胚]]和[[微分同構]]等相關概念)、[[置換群]]、[[投影映射]]及許多其他概念的基本上。 |
|||
# 考虑函数<math>f:\mathbb{R}\rightarrow\mathbb{R}</math>,定义为<math>f(x)=2x+1</math>。这个函数是双射,因为给定任意一个实数<math>y</math>,我们都能解<math>y=2x+1</math>,得到唯一的实数解<math>x=(y-1)/2</math>。 |
|||
# 另外的,函数<math>g:\mathbb{R}\rightarrow\mathbb{R}</math>,定义为<math>f(x)=x^2</math>,这个函数不是双射。这其中有两个实质性的原因。首先,我们有<math>g(1)=1=g(-1)</math>,因此<math>g</math>不是单射;其次,不存在一个实数<math>x</math>满足<math>x^2=-1</math>,所以<math>g</math>也不是满射。不管其中的哪个原因,都足够说明<math>g</math>不是双射。 |
|||
# 但是如果我们用与<math>g</math>同样的式子定义函数<math>h:[0,\infty]\rightarrow[0,\infty]</math>,而且定义域和陪域都限制到非负实数,则这个函数<math>h</math>是双射。这是因为,给定任意的非负实数,我们可以解出<math>y=x^2</math>,得到唯一的非负实数解<math>x=\sqrt{y}</math>。 |
|||
==複合函數與反函數== |
|||
== 性质 == |
|||
一函數<math>f</math>為雙射的若且唯若其[[逆關係]]<math>f^{-1}</math>也是個函數。在這情況,<math>f^{-1}</math>也會是雙射函數。 |
|||
兩個雙射函數<math>f: X \leftrightarrow Y</math>及<math>g : Y \leftrightarrow Z</math>的[[複合函數]]<math>g\circ f</math>亦為雙射函數。其反函數為<math>(g\circ f)^{-1} = (f^{-1})\circ (g^{-1})</math>。 |
|||
* 函数<math>f:X\rightarrow Y</math>是双射当且仅当存在一个函数<math>g:Y\rightarrow X</math>满足<math>g\circ f</math>是一个定义在<math>X</math>上的[[单位函数]]并且<math>f\circ g</math> 是一个定义在<math>Y</math>上的单位函数。当用<math>f</math>可以唯一确定<math>g</math>的时候,我们称<math>g</math>为<math>f</math>的反函数,写作<math>f^{-1}=g</math>。更进一步说,这里的<math>g</math>也是双射,而且<math>g</math>的反函数为<math>f</math>。 |
|||
* 如果<math>f\circ g</math>是双射,则<math>f</math>为双射,<math>g</math>为单射。 |
|||
* 如果<math>f</math>和<math>g</math>皆为双射,则<math>f\circ g</math>也是双射。 |
|||
* 如果<math>X</math>是一个集合,则从<math>X</math>到它自己的一个双射函数,随同函数[[复合运算]]<math>(\circ)</math>,构成一个[[群]],<math>X</math>的[[对称群]],可以用<math>S(X)</math>,<math>S_{X}</math>,或者<math>X!</math>等诸多方法来表示。 |
|||
[[File:Bijective_composition.svg|thumb|300px|一个複合所得的双射,左侧为单射,右侧为满射。]] |
|||
== 相关条目 == |
|||
另一方面,若<math>g\circ f</math>為雙射的,可知<math>f</math>是單射的且<math>g</math>是滿射的,但也僅限於此。 |
|||
一由<math>X</math>至<math>Y</math>的關係<math>f</math>為雙射函數若且唯若存在另一由<math>Y</math>至<math>X</math>的關係<math>g</math>,使得<math>g\circ f</math>為<math>X</math>上的[[恆等函數]],且<math>f\circ g</math>為<math>Y</math>上的[[恆等函數]]。必然地,此兩個集合會有相同的[[势 (数学)|勢]]。 |
|||
*[[置换]] |
|||
*[[单射]] |
|||
==雙射與勢== |
|||
若<math>X</math>和<math>Y</math>為[[有限集合]],則其存在一兩集合的雙射函數[[若且唯若]]兩個集合有相同的元素個數。確實,在[[公理集合論]]裡,這正是「相同元素個數」的''定義'',且廣義化至[[無窮|無限]]集合,並導致了[[基数 (数学)|基數]]的概念,用以分辨[[無限集合]]的不同大小。 |
|||
==例子與反例== |
|||
* 對任一集合<math>X</math>,其[[恆等函數]]為雙射函數。 |
|||
* 函數<math>f : \R\rightarrow\R</math>,其形式為<math>f(x) = 2x + 1</math>,是雙射的,因為對任一<math>y</math>,存在一唯一<math>x = (y - 1)/2</math>使得<math>f(x) = y</math>。 |
|||
* [[指數函數]]<math>g : \R \rightarrow\R</math>,其形式為<math>g(x) = e^{x}</math>,不是雙射的:因為不存在一<math>\R</math>內的<math>x</math>使得<math>g(x) = -1</math>,故<math>g</math>非為雙射。但若其[[到达域|陪域]]改成正實數<math>\R^{+} = (0,+\infty )</math>,則<math>g</math>便是雙射的了;其反函數為[[自然對數]]函數<math>\ln</math>。 |
|||
* 函數<math>h</math> : <math>\R \rightarrow [0,+\infty )</math>,其形式為<math>h(x) = x^2</math>,不是雙射的:因為<math>h(-1) = h(1) = 1</math>,故<math>h</math>非為雙射。但如果把定義域也改成<math>[0,+\infty )</math>,則<math>h</math>便是雙射的了;其反函數為正平方根函數。 |
|||
* <math>\R \to \R : x \mapsto (x-1)x(x+1) = x^3 - x </math>不是雙射函數,因為<math>-1, 0</math>和<math>1</math>都在其定義域裡且都映射至<math>0</math>。 |
|||
* <math>\R \to [-1,1] : x \mapsto \sin(x)</math>不是雙射函數,因為<math>\pi/3</math>和2<math>\pi/3</math>都在其定義域裡且都映射至<math>\sqrt{3}/2</math>。 |
|||
==性質== |
|||
* 一由[[實數]]<math>\mathbb{R}</math>至<math>\mathbb{R}</math>的函數<math>f</math>是雙射的,若且唯若其[[函數圖像|圖像]]和任一水平線相交且只相交於一點。 |
|||
* 設<math>X</math>為一集合,則由<math>X</math>至其本身的雙射函數,加上其複合函數「<math>\circ</math>」的運算,會形成一個[[群]],即為<math>X</math>的[[对称群 (n次对称群)|對稱群]],其標記為<math>\mathfrak{S}(X)</math>、<math>\mathfrak{S}_{X}</math>或<math>X!</math>。 |
|||
* 取一定義域的子集<math>A</math>及一陪域的子集<math>B</math>,則 |
|||
:<math>|f(A)| = |A|</math>且<math>|f^{-1}(B)| = |B|</math>。 |
|||
* 若<math>X</math>和<math>Y</math>為具相同[[势 (数学)|勢]]的[[有限集合]],且<math>f: X \to Y</math>,則下列三種說法是等價的: |
|||
:# <math>f</math>為一雙射函數。 |
|||
:# <math>f</math>為一滿射函數。 |
|||
:# <math>f</math>為一單射函數。 |
|||
* 一个严格的单调函数是双射函数,但双射函数不一定是单调函数(例如<math>y = x^{-3}</math>)。 |
|||
==雙射與範疇論== |
|||
形式上,雙射函數恰好是[[集合範疇]]內的[[同構]]。 |
|||
==另見== |
|||
*[[等势]] |
|||
*[[單射]] |
|||
*[[同構]] |
|||
*[[置換]] |
|||
*[[对称群 (n次对称群)|對稱群]] |
|||
*[[满射]] |
*[[满射]] |
||
*[[雙射計數法]] |
|||
*[[水平线测试]] |
|||
==參考文獻== |
|||
{{refbegin|2}} |
|||
* {{cite book|last=Wolf|title=Proof, Logic and Conjecture: A Mathematician's Toolbox|year=1998|publisher=Freeman}} |
|||
* {{cite book|last=Sundstrom|title=Mathematical Reasoning: Writing and Proof|url=https://archive.org/details/mathematicalreas0000sund|year=2003|publisher=Prentice-Hall}} |
|||
* {{cite book|last1=Smith|last2=Eggen|last3=St.Andre|title=A Transition to Advanced Mathematics (6th Ed.)|year=2006|publisher=Thomson (Brooks/Cole)}} |
|||
* {{cite book|last=Schumacher|title=Chapter Zero: Fundamental Notions of Abstract Mathematics|url=https://archive.org/details/chapterzerofunda0000schu|year=1996|publisher=Addison-Wesley}} |
|||
* {{cite book|last=O'Leary|title=The Structure of Proof: With Logic and Set Theory|year=2003|publisher=Prentice-Hall}} |
|||
* {{cite book|last=Morash|title=Bridge to Abstract Mathematics|publisher=Random House}} |
|||
* {{cite book|last=Maddox|title=Mathematical Thinking and Writing|year=2002|publisher=Harcourt/ Academic Press}} |
|||
* {{cite book|last=Lay|title=Analysis with an introduction to proof|year=2001|publisher=Prentice Hall}} |
|||
* {{cite book|last1=Gilbert|last2=Vanstone|title=An Introduction to Mathematical Thinking|year=2005|publisher=Pearson Prentice-Hall}} |
|||
* {{cite book|last1=Fletcher|last2=Patty|title=Foundations of Higher Mathematics|year=1992|url=https://archive.org/details/foundationsofhig0000flet|publisher=PWS-Kent}} |
|||
* {{cite book|last1=Iglewicz|last2=Stoyle|title=An Introduction to Mathematical Reasoning|publisher=MacMillan}} |
|||
* {{cite book|last=Devlin|first=Keith|title=Sets, Functions, and Logic: An Introduction to Abstract Mathematics|year=2004|publisher=Chapman & Hall/ CRC Press}} |
|||
* {{cite book|last1=D'Angelo|last2=West|title=Mathematical Thinking: Problem Solving and Proofs|url=https://archive.org/details/isbn_8800003757534|year=2000|publisher=Prentice Hall}} |
|||
* {{cite book|last=Cupillari|title=The Nuts and Bolts of Proofs|year=1989|url=https://archive.org/details/nutsboltsofproof00anto|publisher=Wadsworth}} |
|||
* {{cite book|last=Bond|title=Introduction to Abstract Mathematics|publisher=Brooks/Cole}} |
|||
* {{cite book|last1=Barnier|last2=Feldman|title=Introduction to Advanced Mathematics|year=2000|publisher=Prentice Hall}} |
|||
* {{cite book|last=Ash|title=A Primer of Abstract Mathematics|year=1998|url=https://archive.org/details/primerofabstract0000ashr|publisher=MAA}} |
|||
{{refend}} |
|||
==外部連結== |
|||
{{Commons|Category:Bijectivity|Bijectivity}} |
|||
* {{springer|title=Bijection|id=p/b016230}} |
|||
* {{MathWorld|title=Bijection|urlname=Bijection}} |
|||
* [http://jeff560.tripod.com/i.html Earliest Uses of Some of the Words of Mathematics: entry on Injection, Surjection and Bijection has the history of Injection and related terms.]{{Wayback|url=http://jeff560.tripod.com/i.html |date=20170817162925 }} |
|||
{{集合论}} |
|||
[[Category:函数]] |
|||
[[bg:Биекция]] |
|||
[[Category:集合論基本概念]] |
|||
[[cs:Bijekce]] |
|||
[[Category:数学关系]] |
|||
[[de:Bijektivität]] |
|||
[[Category:各类函数]] |
|||
[[en:Bijection, injection and surjection]] |
|||
[[es:Función biyectiva]] |
|||
[[fi:Bijektio]] |
|||
[[fr:Bijection]] |
|||
[[he:התאמה על]] |
|||
[[io:Bijektio]] |
|||
[[it:Corrispondenza biunivoca]] |
|||
[[ja:全単射]] |
|||
[[nl:Bijectie]] |
|||
[[pl:Bijekcja]] |
|||
[[ru:Биекция]] |
|||
[[sv:Bijektiv]] |
|||
[[uk:Бієкція]] |
|||
2024年1月8日 (一) 14:45的最新版本

| 各種函數 |
|---|
| x ↦ f (x) |
| 不同定義域和陪域 |
| 函數類/性質 |
| 構造 |
| 推廣 |
數學中,一個由集合映射至集合的函數,若對每一在內的,存在唯一一個在內的与其对应,且對每一在內的,存在唯一一個在內的与其对应,則此函數為對射函數。
換句話說,如果其為兩集合間的一一對應,则是雙射的。即,同時為單射和滿射。
例如,由整數集合至的函數,其將每一個整數連結至整數,這是一個雙射函數;再看一個例子,函數,其將每一對實數連結至,這也是個雙射函數。
一雙射函數亦簡稱為雙射(英語:bijection)或置換。後者一般較常使用在時。以由至的所有雙射組成的集合標記為。
雙射函數在許多數學領域扮演著很基本的角色,如在同構的定義(以及如同胚和微分同構等相關概念)、置換群、投影映射及許多其他概念的基本上。
複合函數與反函數
[编辑]一函數為雙射的若且唯若其逆關係也是個函數。在這情況,也會是雙射函數。
兩個雙射函數及的複合函數亦為雙射函數。其反函數為。
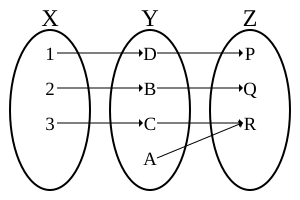
另一方面,若為雙射的,可知是單射的且是滿射的,但也僅限於此。
一由至的關係為雙射函數若且唯若存在另一由至的關係,使得為上的恆等函數,且為上的恆等函數。必然地,此兩個集合會有相同的勢。
雙射與勢
[编辑]若和為有限集合,則其存在一兩集合的雙射函數若且唯若兩個集合有相同的元素個數。確實,在公理集合論裡,這正是「相同元素個數」的定義,且廣義化至無限集合,並導致了基數的概念,用以分辨無限集合的不同大小。
例子與反例
[编辑]- 對任一集合,其恆等函數為雙射函數。
- 函數,其形式為,是雙射的,因為對任一,存在一唯一使得。
- 指數函數,其形式為,不是雙射的:因為不存在一內的使得,故非為雙射。但若其陪域改成正實數,則便是雙射的了;其反函數為自然對數函數。
- 函數 : ,其形式為,不是雙射的:因為,故非為雙射。但如果把定義域也改成,則便是雙射的了;其反函數為正平方根函數。
- 不是雙射函數,因為和都在其定義域裡且都映射至。
- 不是雙射函數,因為和2都在其定義域裡且都映射至。
性質
[编辑]- 一由實數至的函數是雙射的,若且唯若其圖像和任一水平線相交且只相交於一點。
- 設為一集合,則由至其本身的雙射函數,加上其複合函數「」的運算,會形成一個群,即為的對稱群,其標記為、或。
- 取一定義域的子集及一陪域的子集,則
- 且。
- 為一雙射函數。
- 為一滿射函數。
- 為一單射函數。
- 一个严格的单调函数是双射函数,但双射函数不一定是单调函数(例如)。
雙射與範疇論
[编辑]另見
[编辑]參考文獻
[编辑]- Wolf. Proof, Logic and Conjecture: A Mathematician's Toolbox. Freeman. 1998.
- Sundstrom. Mathematical Reasoning: Writing and Proof. Prentice-Hall. 2003.
- Smith; Eggen; St.Andre. A Transition to Advanced Mathematics (6th Ed.). Thomson (Brooks/Cole). 2006.
- Schumacher. Chapter Zero: Fundamental Notions of Abstract Mathematics. Addison-Wesley. 1996.
- O'Leary. The Structure of Proof: With Logic and Set Theory. Prentice-Hall. 2003.
- Morash. Bridge to Abstract Mathematics. Random House.
- Maddox. Mathematical Thinking and Writing. Harcourt/ Academic Press. 2002.
- Lay. Analysis with an introduction to proof. Prentice Hall. 2001.
- Gilbert; Vanstone. An Introduction to Mathematical Thinking. Pearson Prentice-Hall. 2005.
- Fletcher; Patty. Foundations of Higher Mathematics. PWS-Kent. 1992.
- Iglewicz; Stoyle. An Introduction to Mathematical Reasoning. MacMillan.
- Devlin, Keith. Sets, Functions, and Logic: An Introduction to Abstract Mathematics. Chapman & Hall/ CRC Press. 2004.
- D'Angelo; West. Mathematical Thinking: Problem Solving and Proofs. Prentice Hall. 2000.
- Cupillari. The Nuts and Bolts of Proofs. Wadsworth. 1989.
- Bond. Introduction to Abstract Mathematics. Brooks/Cole.
- Barnier; Feldman. Introduction to Advanced Mathematics. Prentice Hall. 2000.
- Ash. A Primer of Abstract Mathematics. MAA. 1998.
外部連結
[编辑]维基共享资源中相关的多媒体资源:Bijectivity














































![{\displaystyle \mathbb {R} \to [-1,1]:x\mapsto \sin(x)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/dbb23cd8a0d8771ac197194b8610e7451013d752)












