双射:修订间差异
外观
删除的内容 添加的内容
Luckas-bot(留言 | 贡献) 小 r2.7.1) (機器人 新增: eu:Bijekzio |
Add 1 book for verifiability (20240107)) #IABot (v2.0.9.5) (GreenC bot |
||
| (未显示24个用户的41个中间版本) | |||
| 第1行: | 第1行: | ||
{{No footnotes|time=2022-04-22T20:29:13+00:00}} |
|||
{{NoteTA|G1=Math|1=zh:雙射;zh-hans:双射;zh-hant:對射}} |
|||
{{NoteTA |
|||
|G1 = Math |
|||
}} |
|||
[[File:Bijection.svg|thumb|200px|一个双射函数]] |
[[File:Bijection.svg|thumb|200px|一个双射函数]] |
||
在[[集合论]]中,一由[[集合]]''X''至集合''Y''的[[函數]]稱為'''雙射'''的,若對每一在''Y''內的''y'',存在唯一一個在''X''內的''x'',使得''f''(''x'')=''y''。 |
|||
{{各種函數}} |
|||
| ⚫ | |||
[[數學]]中,一個由[[集合 (数学)|集合]]<math>X</math>[[映射]]至集合<math>Y</math>的[[函數]],若對每一在<math>Y</math>內的<math>y</math>,存在唯一一個在<math>X</math>內的<math>x</math>与其对应,且對每一在<math>X</math>內的<math>x</math>,存在唯一一個在<math>Y</math>內的<math>y</math>与其对应,則此函數為'''對射函數'''。 |
|||
例如,由[[整數]]集合<math>\Z</math>至<math>\Z</math>的函數succ,其將每一個整數''x''連結至整數succ(''x'')=x+1,及另一函數sumdif,其將每一對實數(''x'',''y'')連結至sumdif(''x'',''y'') = (''x'' + ''y'', ''x'' − ''y'')。 |
|||
| ⚫ | |||
| ⚫ | |||
例如,由[[整數]]集合<math>\Z</math>至<math>\Z</math>的函數<math>\operatorname{succ}</math>,其將每一個整數<math>x</math>連結至整數<math>\operatorname{succ}(x)=x+1</math>,這是一個雙射函數;再看一個例子,函數<math>\operatorname{sumdif}</math>,其將每一對實數<math>(x,y)</math>連結至<math>\operatorname{sumdif}(x,y) = (x + y, x - y)</math>,這也是個雙射函數。 |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
==複合函數與反函數== |
==複合函數與反函數== |
||
一函數 |
一函數<math>f</math>為雙射的若且唯若其[[逆關係]]<math>f^{-1}</math>也是個函數。在這情況,<math>f^{-1}</math>也會是雙射函數。 |
||
兩個雙射函數 |
兩個雙射函數<math>f: X \leftrightarrow Y</math>及<math>g : Y \leftrightarrow Z</math>的[[複合函數]]<math>g\circ f</math>亦為雙射函數。其反函數為<math>(g\circ f)^{-1} = (f^{-1})\circ (g^{-1})</math>。 |
||
[[File:Bijective_composition.svg|thumb|300px|一个双射,左侧为单射,右侧为满射。]] |
[[File:Bijective_composition.svg|thumb|300px|一个複合所得的双射,左侧为单射,右侧为满射。]] |
||
另一方面,若 |
另一方面,若<math>g\circ f</math>為雙射的,可知<math>f</math>是單射的且<math>g</math>是滿射的,但也僅限於此。 |
||
一由 |
一由<math>X</math>至<math>Y</math>的關係<math>f</math>為雙射函數若且唯若存在另一由<math>Y</math>至<math>X</math>的關係<math>g</math>,使得<math>g\circ f</math>為<math>X</math>上的[[恆等函數]],且<math>f\circ g</math>為<math>Y</math>上的[[恆等函數]]。必然地,此兩個集合會有相同的[[势 (数学)|勢]]。 |
||
==雙射與勢== |
==雙射與勢== |
||
若 |
若<math>X</math>和<math>Y</math>為[[有限集合]],則其存在一兩集合的雙射函數[[若且唯若]]兩個集合有相同的元素個數。確實,在[[公理集合論]]裡,這正是「相同元素個數」的''定義'',且廣義化至[[無窮|無限]]集合,並導致了[[基数 (数学)|基數]]的概念,用以分辨[[無限集合]]的不同大小。 |
||
==例子與反例== |
==例子與反例== |
||
* 對任一集合 |
* 對任一集合<math>X</math>,其[[恆等函數]]為雙射函數。 |
||
* 其 |
* 函數<math>f : \R\rightarrow\R</math>,其形式為<math>f(x) = 2x + 1</math>,是雙射的,因為對任一<math>y</math>,存在一唯一<math>x = (y - 1)/2</math>使得<math>f(x) = y</math>。 |
||
* [[指數函數]] |
* [[指數函數]]<math>g : \R \rightarrow\R</math>,其形式為<math>g(x) = e^{x}</math>,不是雙射的:因為不存在一<math>\R</math>內的<math>x</math>使得<math>g(x) = -1</math>,故<math>g</math>非為雙射。但若其[[到达域|陪域]]改成正實數<math>\R^{+} = (0,+\infty )</math>,則<math>g</math>便是雙射的了;其反函數為[[自然對數]]函數<math>\ln</math>。 |
||
* 函數 |
* 函數<math>h</math> : <math>\R \rightarrow [0,+\infty )</math>,其形式為<math>h(x) = x^2</math>,不是雙射的:因為<math>h(-1) = h(1) = 1</math>,故<math>h</math>非為雙射。但如果把定義域也改成<math>[0,+\infty )</math>,則<math>h</math>便是雙射的了;其反函數為正平方根函數。 |
||
* <math>\ |
* <math>\R \to \R : x \mapsto (x-1)x(x+1) = x^3 - x </math>不是雙射函數,因為<math>-1, 0</math>和<math>1</math>都在其定義域裡且都映射至<math>0</math>。 |
||
* <math>\ |
* <math>\R \to [-1,1] : x \mapsto \sin(x)</math>不是雙射函數,因為<math>\pi/3</math>和2<math>\pi/3</math>都在其定義域裡且都映射至<math>\sqrt{3}/2</math>。 |
||
==性質== |
==性質== |
||
* 一由[[實數]] |
* 一由[[實數]]<math>\mathbb{R}</math>至<math>\mathbb{R}</math>的函數<math>f</math>是雙射的,若且唯若其[[函數圖像|圖像]]和任一水平線相交且只相交於一點。 |
||
* 設 |
* 設<math>X</math>為一集合,則由<math>X</math>至其本身的雙射函數,加上其複合函數「<math>\circ</math>」的運算,會形成一個[[群]],即為<math>X</math>的[[对称群 (n次对称群)|對稱群]],其標記為<math>\mathfrak{S}(X)</math>、<math>\mathfrak{S}_{X}</math>或<math>X!</math>。 |
||
* 取一定義域的子集 |
* 取一定義域的子集<math>A</math>及一陪域的子集<math>B</math>,則 |
||
:| |
:<math>|f(A)| = |A|</math>且<math>|f^{-1}(B)| = |B|</math>。 |
||
* 若 |
* 若<math>X</math>和<math>Y</math>為具相同[[势 (数学)|勢]]的[[有限集合]],且<math>f: X \to Y</math>,則下列三種說法是等價的: |
||
:# |
:# <math>f</math>為一雙射函數。 |
||
:# |
:# <math>f</math>為一滿射函數。 |
||
:# |
:# <math>f</math>為一單射函數。 |
||
* 一个严格的单调函数是双射函数,但双射函数不一定是单调函数(例如<math>y = x^{-3}</math>)。 |
|||
==雙射與範疇論== |
==雙射與範疇論== |
||
形式上,雙射函數恰好是 |
形式上,雙射函數恰好是[[集合範疇]]內的[[同構]]。 |
||
==另見== |
==另見== |
||
*[[等势]] |
|||
*[[單射]] |
*[[單射]] |
||
*[[同構]] |
*[[同構]] |
||
*[[置換]] |
*[[置換]] |
||
*[[對稱群]] |
*[[对称群 (n次对称群)|對稱群]] |
||
*[[满射]] |
*[[满射]] |
||
*[[雙射計數法]] |
*[[雙射計數法]] |
||
*[[水平线测试]] |
|||
==參考文獻== |
|||
| ⚫ | |||
{{refbegin|2}} |
|||
| ⚫ | |||
* {{cite book|last=Wolf|title=Proof, Logic and Conjecture: A Mathematician's Toolbox|year=1998|publisher=Freeman}} |
|||
* {{cite book|last=Sundstrom|title=Mathematical Reasoning: Writing and Proof|url=https://archive.org/details/mathematicalreas0000sund|year=2003|publisher=Prentice-Hall}} |
|||
* {{cite book|last1=Smith|last2=Eggen|last3=St.Andre|title=A Transition to Advanced Mathematics (6th Ed.)|year=2006|publisher=Thomson (Brooks/Cole)}} |
|||
* {{cite book|last=Schumacher|title=Chapter Zero: Fundamental Notions of Abstract Mathematics|url=https://archive.org/details/chapterzerofunda0000schu|year=1996|publisher=Addison-Wesley}} |
|||
* {{cite book|last=O'Leary|title=The Structure of Proof: With Logic and Set Theory|year=2003|publisher=Prentice-Hall}} |
|||
* {{cite book|last=Morash|title=Bridge to Abstract Mathematics|publisher=Random House}} |
|||
* {{cite book|last=Maddox|title=Mathematical Thinking and Writing|year=2002|publisher=Harcourt/ Academic Press}} |
|||
* {{cite book|last=Lay|title=Analysis with an introduction to proof|year=2001|publisher=Prentice Hall}} |
|||
* {{cite book|last1=Gilbert|last2=Vanstone|title=An Introduction to Mathematical Thinking|year=2005|publisher=Pearson Prentice-Hall}} |
|||
* {{cite book|last1=Fletcher|last2=Patty|title=Foundations of Higher Mathematics|year=1992|url=https://archive.org/details/foundationsofhig0000flet|publisher=PWS-Kent}} |
|||
* {{cite book|last1=Iglewicz|last2=Stoyle|title=An Introduction to Mathematical Reasoning|publisher=MacMillan}} |
|||
* {{cite book|last=Devlin|first=Keith|title=Sets, Functions, and Logic: An Introduction to Abstract Mathematics|year=2004|publisher=Chapman & Hall/ CRC Press}} |
|||
* {{cite book|last1=D'Angelo|last2=West|title=Mathematical Thinking: Problem Solving and Proofs|url=https://archive.org/details/isbn_8800003757534|year=2000|publisher=Prentice Hall}} |
|||
* {{cite book|last=Cupillari|title=The Nuts and Bolts of Proofs|year=1989|url=https://archive.org/details/nutsboltsofproof00anto|publisher=Wadsworth}} |
|||
* {{cite book|last=Bond|title=Introduction to Abstract Mathematics|publisher=Brooks/Cole}} |
|||
* {{cite book|last1=Barnier|last2=Feldman|title=Introduction to Advanced Mathematics|year=2000|publisher=Prentice Hall}} |
|||
* {{cite book|last=Ash|title=A Primer of Abstract Mathematics|year=1998|url=https://archive.org/details/primerofabstract0000ashr|publisher=MAA}} |
|||
{{refend}} |
|||
==外部連結== |
|||
[[ar:تقابل]] |
|||
{{Commons|Category:Bijectivity|Bijectivity}} |
|||
[[bg:Биекция]] |
|||
* {{springer|title=Bijection|id=p/b016230}} |
|||
[[bs:Bijekcija]] |
|||
* {{MathWorld|title=Bijection|urlname=Bijection}} |
|||
[[ca:Funció bijectiva]] |
|||
* [http://jeff560.tripod.com/i.html Earliest Uses of Some of the Words of Mathematics: entry on Injection, Surjection and Bijection has the history of Injection and related terms.]{{Wayback|url=http://jeff560.tripod.com/i.html |date=20170817162925 }} |
|||
[[cs:Bijekce]] |
|||
[[da:Bijektiv]] |
|||
{{集合论}} |
|||
[[de:Bijektive Funktion]] |
|||
[[en:Bijection]] |
|||
[[ |
[[Category:函数]] |
||
| ⚫ | |||
[[es:Función biyectiva]] |
|||
[[Category:数学关系]] |
|||
[[eu:Bijekzio]] |
|||
| ⚫ | |||
[[fa:تابع دوسویی]] |
|||
[[fi:Bijektio]] |
|||
[[fr:Bijection]] |
|||
[[he:פונקציה חד-חד-ערכית ועל]] |
|||
[[hr:Bijekcija]] |
|||
[[hu:Bijekció]] |
|||
[[io:Bijektio]] |
|||
[[is:Gagntæk vörpun]] |
|||
[[it:Corrispondenza biunivoca]] |
|||
[[ja:全単射]] |
|||
[[ko:전단사함수]] |
|||
[[lmo:Bigezziú]] |
|||
[[lt:Bijekcija]] |
|||
[[nl:Bijectie]] |
|||
[[nn:Bijeksjon]] |
|||
[[no:Bijeksjon]] |
|||
[[oc:Bijeccion]] |
|||
[[pl:Funkcja wzajemnie jednoznaczna]] |
|||
[[pt:Função bijectiva]] |
|||
[[ru:Биекция]] |
|||
[[sk:Bijektívne zobrazenie]] |
|||
[[sl:Bijektivna preslikava]] |
|||
[[sr:Бијекција]] |
|||
[[sv:Bijektiv funktion]] |
|||
[[th:ฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง]] |
|||
[[uk:Бієкція]] |
|||
[[vi:Song ánh]] |
|||
2024年1月8日 (一) 14:45的最新版本

| 各種函數 |
|---|
| x ↦ f (x) |
| 不同定義域和陪域 |
| 函數類/性質 |
| 構造 |
| 推廣 |
數學中,一個由集合映射至集合的函數,若對每一在內的,存在唯一一個在內的与其对应,且對每一在內的,存在唯一一個在內的与其对应,則此函數為對射函數。
換句話說,如果其為兩集合間的一一對應,则是雙射的。即,同時為單射和滿射。
例如,由整數集合至的函數,其將每一個整數連結至整數,這是一個雙射函數;再看一個例子,函數,其將每一對實數連結至,這也是個雙射函數。
一雙射函數亦簡稱為雙射(英語:bijection)或置換。後者一般較常使用在時。以由至的所有雙射組成的集合標記為。
雙射函數在許多數學領域扮演著很基本的角色,如在同構的定義(以及如同胚和微分同構等相關概念)、置換群、投影映射及許多其他概念的基本上。
複合函數與反函數
[编辑]一函數為雙射的若且唯若其逆關係也是個函數。在這情況,也會是雙射函數。
兩個雙射函數及的複合函數亦為雙射函數。其反函數為。
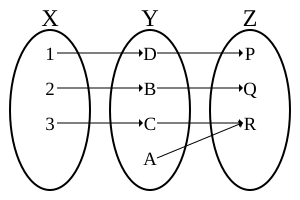
另一方面,若為雙射的,可知是單射的且是滿射的,但也僅限於此。
一由至的關係為雙射函數若且唯若存在另一由至的關係,使得為上的恆等函數,且為上的恆等函數。必然地,此兩個集合會有相同的勢。
雙射與勢
[编辑]若和為有限集合,則其存在一兩集合的雙射函數若且唯若兩個集合有相同的元素個數。確實,在公理集合論裡,這正是「相同元素個數」的定義,且廣義化至無限集合,並導致了基數的概念,用以分辨無限集合的不同大小。
例子與反例
[编辑]- 對任一集合,其恆等函數為雙射函數。
- 函數,其形式為,是雙射的,因為對任一,存在一唯一使得。
- 指數函數,其形式為,不是雙射的:因為不存在一內的使得,故非為雙射。但若其陪域改成正實數,則便是雙射的了;其反函數為自然對數函數。
- 函數 : ,其形式為,不是雙射的:因為,故非為雙射。但如果把定義域也改成,則便是雙射的了;其反函數為正平方根函數。
- 不是雙射函數,因為和都在其定義域裡且都映射至。
- 不是雙射函數,因為和2都在其定義域裡且都映射至。
性質
[编辑]- 一由實數至的函數是雙射的,若且唯若其圖像和任一水平線相交且只相交於一點。
- 設為一集合,則由至其本身的雙射函數,加上其複合函數「」的運算,會形成一個群,即為的對稱群,其標記為、或。
- 取一定義域的子集及一陪域的子集,則
- 且。
- 為一雙射函數。
- 為一滿射函數。
- 為一單射函數。
- 一个严格的单调函数是双射函数,但双射函数不一定是单调函数(例如)。
雙射與範疇論
[编辑]另見
[编辑]參考文獻
[编辑]- Wolf. Proof, Logic and Conjecture: A Mathematician's Toolbox. Freeman. 1998.
- Sundstrom. Mathematical Reasoning: Writing and Proof. Prentice-Hall. 2003.
- Smith; Eggen; St.Andre. A Transition to Advanced Mathematics (6th Ed.). Thomson (Brooks/Cole). 2006.
- Schumacher. Chapter Zero: Fundamental Notions of Abstract Mathematics. Addison-Wesley. 1996.
- O'Leary. The Structure of Proof: With Logic and Set Theory. Prentice-Hall. 2003.
- Morash. Bridge to Abstract Mathematics. Random House.
- Maddox. Mathematical Thinking and Writing. Harcourt/ Academic Press. 2002.
- Lay. Analysis with an introduction to proof. Prentice Hall. 2001.
- Gilbert; Vanstone. An Introduction to Mathematical Thinking. Pearson Prentice-Hall. 2005.
- Fletcher; Patty. Foundations of Higher Mathematics. PWS-Kent. 1992.
- Iglewicz; Stoyle. An Introduction to Mathematical Reasoning. MacMillan.
- Devlin, Keith. Sets, Functions, and Logic: An Introduction to Abstract Mathematics. Chapman & Hall/ CRC Press. 2004.
- D'Angelo; West. Mathematical Thinking: Problem Solving and Proofs. Prentice Hall. 2000.
- Cupillari. The Nuts and Bolts of Proofs. Wadsworth. 1989.
- Bond. Introduction to Abstract Mathematics. Brooks/Cole.
- Barnier; Feldman. Introduction to Advanced Mathematics. Prentice Hall. 2000.
- Ash. A Primer of Abstract Mathematics. MAA. 1998.
外部連結
[编辑]维基共享资源中相关的多媒体资源:Bijectivity














































![{\displaystyle \mathbb {R} \to [-1,1]:x\mapsto \sin(x)}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/dbb23cd8a0d8771ac197194b8610e7451013d752)












