施泰纳-莱穆斯定理:修订间差异
无编辑摘要 |
Add 1 book for verifiability (20240207)) #IABot (v2.0.9.5) (GreenC bot |
||
| (未显示8个用户的20个中间版本) | |||
| 第1行: | 第1行: | ||
[[File:Steiner-Lehmus.png|thumb|right| |
[[File:Steiner-Lehmus.png|thumb|right|200px|<math>\alpha=\beta ,\;\gamma=\delta ,\;AE=BD</math><math>\;\Rightarrow\;</math><math>\triangle ABC</math>是等腰三角形]] |
||
'''施泰纳-莱穆斯定理'''(Steiner–Lehmus theorem)是[[平面几何]]的一个定理:两条[[角平分线|内角平分线]]相等的[[三角形]]是[[等腰三角形]]。该命题看似显而易见,但直到19世纪上半叶才得到明确的几何证明,随后成为平面几何领域最受欢迎的证明题之一。该定理以德国数学家{{tsl|en|C. L. Lehmus|C·L·莱穆斯}}和瑞士数学家{{tsl|en|Jakob Steiner|雅各布·施泰纳}}命名,两人在通信中最早提出和解决了该问题。 |
|||
\gamma=\delta </math> <math>\Rightarrow \triangle ABC </math>是等腰三角形]] |
|||
'''斯坦納-雷姆斯定理'''說明:有[[三角形]]''ABC'',''D''、''E''點分別在''AC''、''BC''上,使得''BD''、''AE''分別為角''ABC''及角''BAC''的內角平分線。若''BD=AE'',则''BC=AC''。 |
|||
施泰纳-莱穆斯定理的结论并不能推广到[[外角]]平分线上。也就是说,两条外角平分线相等的三角形不一定是等腰三角形。 |
|||
類似的陳述適用於中線、高、內角''n''分線(將原來的角分成原來的''1/n''角的線段)和經過{{tsl|en|Gergonne point|葛爾剛點}}的線[http://forumgeom.fau.edu/FG2005volume5/FG200525.pdf]等的[[塞瓦定理|塞瓦線段]]。可是這並不適用於外角平分線。一個132度、36度和12度的三角形是一個反例。 |
|||
==历史== |
|||
這個定理是{{tsl|en|C. L. Lehmus|鲁道夫·雷姆斯}}(Ludolph Lehmus)向{{tsl|en|Jakob Steiner|-{zh-hans:雅各布·斯坦納; zh-hant:雅可比·斯坦納}-}}提出的。 |
|||
在[[平面几何]]中,“[[等腰三角形]]的两条[[角平分线|内角平分线]]相等”,是一个非常容易得到的结论。该命题的[[逆命题]],“两条内角平分线相等的三角形是等腰三角形”,则没有看上去那么容易证明。1840年,[[德国]]数学家{{tsl|en|C. L. Lehmus|C·L·莱穆斯}}写信给瑞士数学家、几何学权威{{tsl|en|Jakob Steiner|雅各布·施泰纳}},询问是否能给出一个纯几何的证明。施泰纳解决了问题,不过直到1844年才公开发表。第一个公开证明来自法国[[路易大帝中学]]的学生鲁热万(Rougevin),发表在1842年的《{{link-fr|新数学年鉴|Nouvelles annales de mathématiques}}》上。1850年,莱穆斯也给出了自己的证明。<ref>{{cite journal|journal=''Nouvelles annales de mathématiques: journal des candidats aux écoles polytechnique et normale''|volume=1|year=1842|page=138-139|title=Démonstration du théorème 1 (page 57)|author=Rougevin|language=fr|url=http://www.numdam.org/item/NAM_1842_1_1__138_0.pdf|access-date=2023-06-11|archive-date=2023-06-11|archive-url=https://web.archive.org/web/20230611074406/http://www.numdam.org/item/NAM_1842_1_1__138_0.pdf|dead-url=no}}</ref><ref>{{cite journal|author=Steiner|first=J.|title=Elementare Lösung einer Aufgabe über das ebene und sphärische Dreieck|journal=''Journal für die reine und angewandte Mathematik''|volume=28|year=1844|page=375-379|url=https://eudml.org/doc/147256|language=de|access-date=2023-06-11|archive-date=2023-06-11|archive-url=https://web.archive.org/web/20230611074337/https://eudml.org/doc/147256|dead-url=no}}</ref><ref>{{cite journal|author=M'Bride|first=J.|year=1943|title=“The equal internal bisectors theorem, 1840-1940. … Many solutions or none?”: A centenary account|journal=''Edinburgh Mathematical Notes''|volume=33|page=1-13|doi=10.1017/S0950184300000021|url=https://www.cambridge.org/core/services/aop-cambridge-core/content/view/7B625B08567935CAE06A0AC9430477C0/S0950184300000021a.pdf/div-class-title-the-equal-internal-bisectors-theorem-1840-1940-many-solutions-or-none-a-centenary-account-div.pdf|language=en|access-date=2023-06-11|archive-date=2019-05-02|archive-url=https://web.archive.org/web/20190502185208/https://www.cambridge.org/core/services/aop-cambridge-core/content/view/7B625B08567935CAE06A0AC9430477C0/S0950184300000021a.pdf/div-class-title-the-equal-internal-bisectors-theorem-1840-1940-many-solutions-or-none-a-centenary-account-div.pdf|dead-url=unfit}}</ref><ref>{{cite book|title=Geometry Revisited|first1=H. S. M.|last1=Coxeter|first2=S. L.|last2=Greitzer|url=https://www.math.unipd.it/~legovini/Coxeter_Greitzer_Geometry_revisited.pdf|publisher=The Mathematical Association of America|year=1967|location=Washington, D.C.|isbn=0-88385-619-0|page=14-16|language=en|access-date=2023-06-11|archive-date=2023-01-28|archive-url=https://web.archive.org/web/20230128170326/https://www.math.unipd.it/~legovini/Coxeter_Greitzer_Geometry_revisited.pdf|dead-url=no}}</ref><ref name=sauve>{{cite journal|first=Léo|last=Sauvé|title=The Steiner-Lehmus theorem|journal=''Eureka''|volume=2|year=1976|page=19-24|url=https://cms.math.ca/wp-content/uploads/crux-pdfs/Crux_v2n02_Feb.pdf|language=en|access-date=2023-06-17|archive-date=2022-04-19|archive-url=https://web.archive.org/web/20220419204049/https://cms.math.ca/wp-content/uploads/crux-pdfs/Crux_v2n02_Feb.pdf|dead-url=no}}</ref> |
|||
19世纪40年代起的一百多年里,关于施泰纳-莱穆斯定理的几何证明大量涌现,有上百个之多。绝大多数证明都依赖于[[反证法]],即先假定两内角平分线相等的三角形不等腰,其中一个内角大于另一个,然后推出矛盾的结论。于是,关注点变成了,施泰纳-莱穆斯定理是否有“直接”的几何证明法,以及怎样的证明才算得上是“直接”。不过也有人认为,拒绝反证法的“纯粹主义”并没有什么意义。<ref name=sauve/> |
|||
==外部連結== |
|||
* [http://www.umanitoba.ca/science/mathematics/undergrad_info/Issue6.pdf The Lasting Legacy of Ludoph Lehmus, Diane and Roy Dowling] |
|||
==证明== |
|||
* [http://www.pandd.demon.nl/steileh.htm Stelling van Steiner-Lehmus]:不同的證法(有圖,荷蘭語) |
|||
===反证法=== |
|||
* [http://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/steiner-lehmus 不同的證法](純文字,英語) |
|||
[[File:施泰纳-莱穆斯定理证明 01.svg|thumb|反证法]] |
|||
在 <math>\triangle ABC</math> 中,两条内角平分线 <math>CE = BD</math> 。 |
|||
假设 <math>\angle ABC \neq \angle ACB</math> ,令 <math>\angle ABC = 2\alpha < \angle ACB = 2\beta</math> 。 |
|||
在线段 <math>AB</math> 上取点 <math>G</math>,使 <math>\angle ECG = \alpha </math>, <math>CG</math> 交 <math>BD</math> 于点 <math>F</math> 。 |
|||
:<math>\triangle CEG \sim \triangle BFG</math><math>\;\Rightarrow \;</math><math>{CG \over BG} = {CE \over BF} = {BD \over BF} > 1</math><math>\;\Rightarrow \;</math><math>CG > BG </math><math>\;\Rightarrow \;</math><math>\angle CBG > \angle BCG</math><math>\;\Rightarrow \;</math><math>\alpha > \beta</math> |
|||
结论与假设矛盾,故假设不成立。故 <math>\angle ABC = \angle ACB</math> 。<ref name=sauve/> |
|||
===直接证明=== |
|||
[[File:施泰纳-莱穆斯定理证明 02.svg|thumb|直接证明法]] |
|||
在 <math>\triangle ABC</math> 中,两条内角平分线 <math>BE = CD</math> 。记 <math>\angle CBE = \angle ABE = \alpha</math> ,<math>\angle BCD = \angle ACD = \beta</math> 。 |
|||
做直线 <math>EF</math> ,使 <math>\angle BEF = \beta </math>。做直线 <math>BF</math> ,使 <math>\angle EBF = \angle CDB = 180^\circ - 2\alpha - \beta</math> 。 |
|||
:<math>\triangle BEF \cong \triangle DCB</math><math>\;\Rightarrow \;</math><math> |
|||
\begin{cases} |
|||
BF = DB \\ |
|||
EF = CB \\ |
|||
\end{cases} |
|||
</math> |
|||
:<math> |
|||
\begin{cases} |
|||
EF = CB \\ |
|||
CF = CF \\ |
|||
\angle CBF = \angle FEC = 180^\circ - \alpha - \beta > 90^\circ \\ |
|||
\end{cases} |
|||
</math><math>\;\Rightarrow \;</math><math>\triangle CBF \cong \triangle FEC</math><math>\;\Rightarrow \;</math><math>BF = EC</math> |
|||
:<math>EC = BF = DB</math><math>\;\Rightarrow \;</math><math>\triangle DBC \cong \triangle ECB</math><math>\;\Rightarrow \;</math><math>\angle ABC = \angle ACB</math> |
|||
该证明方法由F. G. Hesse于1874年发表。不过,该证明方法所用到的一些构造和定理,如“三角形内角和为180度”,本身需要用反证法去证明,因此一些纯粹主义者认为这一证明还是不够直接。<ref>{{cite thesis|last=Gardner|first=Sherri R.|title=''A Variety of Proofs of the Steiner-Lehmus Theorem''|year=2013|degree=Master of Science|language=en|publisher=East Tennessee State University|url=https://dc.etsu.edu/cgi/viewcontent.cgi?article=2332&context=etd|page=19|access-date=2023-06-25|archive-date=2023-06-27|archive-url=https://web.archive.org/web/20230627123239/https://dc.etsu.edu/cgi/viewcontent.cgi?article=2332&context=etd|dead-url=no}}</ref> |
|||
===代数证明=== |
|||
利用[[角平分線長公式]],可以简洁地证明施泰纳-莱穆斯定理。<ref name=trigg>{{cite book|title=''Mathematical Quickies''|url=https://archive.org/details/mathematicalquic0000trig|first=Charles W.|last=Trigg|publisher=Dover Publications|location=New York|date=1985|orig-year=1967|isbn=0-486-24949-2|page=[https://archive.org/details/mathematicalquic0000trig/page/103 103]|language=en}}</ref> |
|||
:<math>t_a=t_b \ \,\Rightarrow\ \,\sqrt{bc (1-{a^2 \over (b+c)^2})}=\sqrt{ac (1-{b^2 \over (a+c)^2})}</math> |
|||
化简后得到: <math>c(a+b+c)(a-b)[(a+b)(c^2+ab)+3abc+c^3]=0</math> |
|||
连乘的其他各项都为正数,从而推出: <math>a-b=0</math> |
|||
==外角平分线问题== |
|||
[[File:外角平分线相等的三角形.svg|thumb|两条外角平分线相等的不等腰三角形。易证 <math>AD=AB=BE</math>|250px]] |
|||
施泰纳-莱穆斯定理的结论并不能推广到[[外角]]平分线上。也就是说,两条外角平分线相等的三角形不一定是等腰三角形。一个常举的反例是三个内角分别为132度、36度和12度的三角形,因为这个三角形的两条外角平分线恰等于一条边,易于证明。<ref name=Trigg>{{cite journal|first=Charles W.|last=Trigg|title=Problem 862, Solution I|journal=''Mathematics Magazine''|year=1974|volume=1|issue=1|page=52-53|language=en|doi=10.2307/2688766|url=http://math.fau.edu/yiu/PSRM2015/yiu/New%20Folder%20(4)/MGProblems/MGProblems47(74)1.pdf|access-date=2023-06-11|archive-date=2022-02-13|archive-url=https://web.archive.org/web/20220213224255/http://math.fau.edu/yiu/PSRM2015/yiu/New%20Folder%20(4)/MGProblems/MGProblems47(74)1.pdf|dead-url=no}}</ref> |
|||
进一步地,数学家们尝试证明,所有两条外角平分线相等的不等腰三角形的共性。<ref name=Trigg/><ref>{{cite book|title=分角线相等的三角形:初等几何机器证明问题|author=[[吴文俊]]|author2=吕学礼|publisher=人民教育出版社|location=北京|year=1985|ISBN=9780070120723}}</ref>中国数学家蒋声指出,满足下列条件的三角形都是有两条外角平分线相等的不等腰三角形:<ref>{{cite journal|author=蒋声|title=有两条外角平分线相等的不等边三角形|journal=中等数学|year=1989|issue=01|page=12-13}}</ref> |
|||
:<math> |
|||
\begin{cases} |
|||
A = \theta - \arccos(1+\cos \theta + \cos 2 \theta) \\ |
|||
B = \theta + \arccos(1+\cos \theta + \cos 2 \theta) \\ |
|||
C = 180^\circ - 2 \theta \\ |
|||
60^\circ < \theta < 90^\circ \\ |
|||
\end{cases} |
|||
</math> |
|||
“两条外角平分线相等的三角形是等腰三角形”是假命题,不过较弱的命题是成立的:三角形的两个角的外角平分线相等,若第三个角是最大或最小的角,则该三角形是等腰三角形;不然,则不是等腰三角形。<ref>{{cite journal|last=叶余本|title=続.二等辺三角形の性質の一つの研究|journal=日本数学教育学会誌|volume=66|issue=11|year=1984|page=45-49|doi=10.32296/jjsme.66.11_45|url=https://www.jstage.jst.go.jp/article/jjsme/66/11/66_45/_pdf|access-date=2023-06-11|archive-date=2023-06-11|archive-url=https://web.archive.org/web/20230611154839/https://www.jstage.jst.go.jp/article/jjsme/66/11/66_45/_pdf|dead-url=no}}</ref> |
|||
==参考文献== |
|||
{{reflist}} |
|||
[[Category:几何定理|S]] |
[[Category:几何定理|S]] |
||
2024年2月8日 (四) 08:19的最新版本

施泰纳-莱穆斯定理(Steiner–Lehmus theorem)是平面几何的一个定理:两条内角平分线相等的三角形是等腰三角形。该命题看似显而易见,但直到19世纪上半叶才得到明确的几何证明,随后成为平面几何领域最受欢迎的证明题之一。该定理以德国数学家C·L·莱穆斯和瑞士数学家雅各布·施泰纳命名,两人在通信中最早提出和解决了该问题。
施泰纳-莱穆斯定理的结论并不能推广到外角平分线上。也就是说,两条外角平分线相等的三角形不一定是等腰三角形。
历史
[编辑]在平面几何中,“等腰三角形的两条内角平分线相等”,是一个非常容易得到的结论。该命题的逆命题,“两条内角平分线相等的三角形是等腰三角形”,则没有看上去那么容易证明。1840年,德国数学家C·L·莱穆斯写信给瑞士数学家、几何学权威雅各布·施泰纳,询问是否能给出一个纯几何的证明。施泰纳解决了问题,不过直到1844年才公开发表。第一个公开证明来自法国路易大帝中学的学生鲁热万(Rougevin),发表在1842年的《新数学年鉴》上。1850年,莱穆斯也给出了自己的证明。[1][2][3][4][5]
19世纪40年代起的一百多年里,关于施泰纳-莱穆斯定理的几何证明大量涌现,有上百个之多。绝大多数证明都依赖于反证法,即先假定两内角平分线相等的三角形不等腰,其中一个内角大于另一个,然后推出矛盾的结论。于是,关注点变成了,施泰纳-莱穆斯定理是否有“直接”的几何证明法,以及怎样的证明才算得上是“直接”。不过也有人认为,拒绝反证法的“纯粹主义”并没有什么意义。[5]
证明
[编辑]反证法
[编辑]
在 中,两条内角平分线 。
假设 ,令 。
在线段 上取点 ,使 , 交 于点 。
结论与假设矛盾,故假设不成立。故 。[5]
直接证明
[编辑]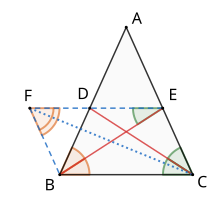
在 中,两条内角平分线 。记 , 。
做直线 ,使 。做直线 ,使 。
该证明方法由F. G. Hesse于1874年发表。不过,该证明方法所用到的一些构造和定理,如“三角形内角和为180度”,本身需要用反证法去证明,因此一些纯粹主义者认为这一证明还是不够直接。[6]
代数证明
[编辑]利用角平分線長公式,可以简洁地证明施泰纳-莱穆斯定理。[7]
化简后得到:
连乘的其他各项都为正数,从而推出:
外角平分线问题
[编辑]
施泰纳-莱穆斯定理的结论并不能推广到外角平分线上。也就是说,两条外角平分线相等的三角形不一定是等腰三角形。一个常举的反例是三个内角分别为132度、36度和12度的三角形,因为这个三角形的两条外角平分线恰等于一条边,易于证明。[8]
进一步地,数学家们尝试证明,所有两条外角平分线相等的不等腰三角形的共性。[8][9]中国数学家蒋声指出,满足下列条件的三角形都是有两条外角平分线相等的不等腰三角形:[10]
“两条外角平分线相等的三角形是等腰三角形”是假命题,不过较弱的命题是成立的:三角形的两个角的外角平分线相等,若第三个角是最大或最小的角,则该三角形是等腰三角形;不然,则不是等腰三角形。[11]
参考文献
[编辑]- ^ Rougevin. Démonstration du théorème 1 (page 57) (PDF). Nouvelles annales de mathématiques: journal des candidats aux écoles polytechnique et normale. 1842, 1: 138-139 [2023-06-11]. (原始内容存档 (PDF)于2023-06-11) (法语).
- ^ Steiner, J. Elementare Lösung einer Aufgabe über das ebene und sphärische Dreieck. Journal für die reine und angewandte Mathematik. 1844, 28: 375-379 [2023-06-11]. (原始内容存档于2023-06-11) (德语).
- ^ M'Bride, J. “The equal internal bisectors theorem, 1840-1940. … Many solutions or none?”: A centenary account (PDF). Edinburgh Mathematical Notes. 1943, 33: 1-13 [2023-06-11]. doi:10.1017/S0950184300000021. 原始内容存档于2019-05-02 (英语).
- ^ Coxeter, H. S. M.; Greitzer, S. L. Geometry Revisited (PDF). Washington, D.C.: The Mathematical Association of America. 1967: 14-16 [2023-06-11]. ISBN 0-88385-619-0. (原始内容存档 (PDF)于2023-01-28) (英语).
- ^ 5.0 5.1 5.2 Sauvé, Léo. The Steiner-Lehmus theorem (PDF). Eureka. 1976, 2: 19-24 [2023-06-17]. (原始内容存档 (PDF)于2022-04-19) (英语).
- ^ Gardner, Sherri R. A Variety of Proofs of the Steiner-Lehmus Theorem (Master of Science论文). East Tennessee State University: 19. 2013 [2023-06-25]. (原始内容存档于2023-06-27) (英语).
- ^ Trigg, Charles W. Mathematical Quickies. New York: Dover Publications. 1985: 103 [1967]. ISBN 0-486-24949-2 (英语).
- ^ 8.0 8.1 Trigg, Charles W. Problem 862, Solution I (PDF). Mathematics Magazine. 1974, 1 (1): 52-53 [2023-06-11]. doi:10.2307/2688766. (原始内容存档 (PDF)于2022-02-13) (英语).
- ^ 吴文俊; 吕学礼. 分角线相等的三角形:初等几何机器证明问题. 北京: 人民教育出版社. 1985. ISBN 9780070120723.
- ^ 蒋声. 有两条外角平分线相等的不等边三角形. 中等数学. 1989, (01): 12-13.
- ^ 叶余本. 続.二等辺三角形の性質の一つの研究. 日本数学教育学会誌. 1984, 66 (11): 45-49 [2023-06-11]. doi:10.32296/jjsme.66.11_45. (原始内容存档于2023-06-11).


































![{\displaystyle c(a+b+c)(a-b)[(a+b)(c^{2}+ab)+3abc+c^{3}]=0}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/13f64c4a0b186374e7fb265b024d1fa965f18391)


