最小二乘法

使用二次函数拟合一组数据点的结果

最小二乘法（英語：least squares method），又称最小平方法，是一种數學優化建模方法。它通过最小化誤差的平方和尋找數據的最佳函數匹配。

利用最小二乘法可以簡便的求得未知的數據，並使得求得的數據與實際數據之間誤差的平方和為最小。

“最小平方法”是對線性方程組，即方程個數比未知數更多的方程組，以迴歸分析求得近似解的標準方法。在這整個解決方案中，最小平方法演算為每一方程式的結果中，將殘差平方和的總和最小化。

最重要的應用是在曲線擬合上。最小平方所涵義的最佳擬合，即殘差（殘差為：觀測值與模型提供的擬合值之間的差距）平方總和的最小化。當問題在自變量（x變量）有重大不確定性時，那麼使用簡易迴歸和最小平方法會發生問題；在這種情況下，須另外考慮變量-誤差-擬合模型所需的方法，而不是最小平方法。

最小平方問題分為兩種：線性或普通的最小平方法，和非線性的最小平方法，取決於在所有未知數中的殘差是否為線性。線性的最小平方問題發生在統計迴歸分析中；它有一個封閉形式的解決方案。非線性的問題通常經由迭代細緻化來解決；在每次迭代中，系統由線性近似，因此在這兩種情況下核心演算是相同的。

最小平方法所得出的多項式，即以擬合曲線的函數來描述自變量與預計應變量的變異數關係。

當觀測值來自指數族且滿足輕度條件時，最小平方估計和最大似然估計是相同的。最小平方法也能從動差法得出。

以下討論大多是以線性函數形式來表示，但對於更廣泛的函數族，最小平方法也是有效和實用的。此外，迭代地將局部的二次近似應用於或然性（藉由費雪信息），最小平方法可用於擬合廣義線性模型。

最小平方法通常歸功於高斯（Carl Friedrich Gauss，1795），但最小平方法是由阿德里安-马里·勒让德（Adrien-Marie Legendre）首先發表的。

歷史背景

最小平方法發展於天文學和大地測量學領域，科學家和數學家嘗試為大航海探索時期的海洋航行挑戰提供解決方案。準確描述天體的行為是船艦在大海洋上航行的關鍵，水手不能再依靠陸上目標導航作航行。

這個方法是在十八世紀期間一些進步的集大成：

• 不同觀測值的組合是真實值的最佳估計；多次觀測會減少誤差而不是增加，也許在1722年由Roger Cotes首先闡明。

• 在相同條件下採取的不同觀察結果，與只嘗試記錄一次最精確的觀察結果是對立的。這個方法被稱為平均值方法。托馬斯·馬耶爾（Tobias Mayer）在1750年研究月球的天平動時，特別使用這種方法，而拉普拉斯（Pierre-Simon Laplace）在1788年他的工作成果中以此解釋木星和土星的運動差異。

• 在不同條件下進行的不同觀測值組合。該方法被稱為最小絕對偏差法，出現在Roger Joseph Boscovich在1757年他對地球形體的著名作品，而拉普拉斯在1799年也表示了同樣的問題。

• 評定對誤差達到最小的解決方案標準，拉普拉斯指明了誤差的概率密度的數學形式，並定義了誤差最小化的估計方法。為此，拉普拉斯使用了一雙邊對稱的指數分佈，現在稱為拉普拉斯分佈作為誤差分佈的模型，並將絕對偏差之和作為估計誤差。他認為這是他最簡單的假設，他期待得出算術平均值而成為最佳的估計。可相反地，他的估計是後驗中位數。

最小平方法

高斯

1801年，意大利天文學家朱塞普·皮亞齊發現了第一顆小行星谷神星。经过40天的追蹤觀測後，由於谷神星運行至太陽背後，使得皮亞齊失去了谷神星的位置。隨後全世界的科學家利用皮亞齊的觀測數據開始尋找谷神星，但是根據大多数人計算的结果来尋找谷神星都沒有结果。當年24歲的高斯也計算了谷神星的軌道。奥地利天文學家海因里希·奥伯斯根據高斯計算出来的軌道重新發現了谷神星。

高斯使用的最小平方法的方法發表於1809年他的著作《天體運動論》中，而法國科學家勒壤得于1806年獨立發現“最小平方法”，但因不為世人所知而默默無聞。兩人曾為誰最早創立最小平方法原理發生爭執。

1829年，高斯提供了最小平方法的優化效果強於其他方法的證明，見高斯-马尔可夫定理。

示例

数据点（红色）、使用最小二乘法求得的最佳解（蓝色）、误差（绿色）。

某次實驗得到了四個數據點 $(x,y)$：$(1,6)$、$(2,5)$、$(3,7)$、$(4,10)$（右圖紅色的點）。我們希望找出一條和這四個點最匹配的直線 $y=\beta _{2}x+\beta _{1}$，即找出在某種「最佳情况」下能夠大致符合如下超定線性方程组的 $\beta _{1}$ 和 $\beta _{2}$：

${\begin{alignedat}{4}\beta _{1}+1\beta _{2}&&\;=\;&&6&\\\beta _{1}+2\beta _{2}&&\;=\;&&5&\\\beta _{1}+3\beta _{2}&&\;=\;&&7&\\\beta _{1}+4\beta _{2}&&\;=\;&&10&\\\end{alignedat}}$

最小平方法採用的方法是盡量使得等號兩邊差的平方最小，也就是找出這個函數的最小值：

${\begin{aligned}S(\beta _{1},\beta _{2})=&\left[6-(\beta _{1}+1\beta _{2})\right]^{2}+\left[5-(\beta _{1}+2\beta _{2})\right]^{2}\\&+\left[7-(\beta _{1}+3\beta _{2})\right]^{2}+\left[10-(\beta _{1}+4\beta _{2})\right]^{2}.\\\end{aligned}}$

最小值可以通过对 $S(\beta _{1},\beta _{2})$ 分别求 $\beta _{1}$ 和 $\beta _{2}$ 的偏導數，然後使他們等於零得到。

${\frac {\partial S}{\partial \beta _{1}}}=0=8\beta _{1}+20\beta _{2}-56$

${\frac {\partial S}{\partial \beta _{2}}}=0=20\beta _{1}+60\beta _{2}-154.$

如此就得到了一个只有两个未知数的方程组，很容易就可以解出：

$\beta _{1}=3.5$

$\beta _{2}=1.4$

也就是说直线 $y=3.5+1.4x$ 是最佳的。

方法

人们对由某一变量$t$ 或多个变量$t_{1}$……$t_{n}$ 构成的相关变量$y$感兴趣。如弹簧的形变与所用的力相关，一个企业的盈利与其营业额，投资收益和原始资本有关。为了得到这些变量同$y$之间的关系，便用不相关变量去构建$y$，使用如下函数模型

$y_{m}=f(t_{1},\dots ,t_{q};b_{1},\dots ,b_{p})$,

$q$个獨立变量或$p$个係數去拟合。

通常人们将一个可能的、对不相关变量t的构成都无困难的函数类型称作函数模型（如抛物线函数或指数函数）。参数b是为了使所选择的函数模型同观测值y相匹配。（如在测量弹簧形变时，必须将所用的力与弹簧的膨胀系数联系起来）。其目标是合适地选择参数，使函数模型最好的拟合观测值。一般情况下，观测值远多於所选择的参数。

其次的问题是怎样判断不同拟合的质量。高斯和勒让德的方法是，假设测量误差的平均值为0。令每一个测量误差对应一个变量并与其它测量误差不相关（随机无关）。人们假设，在测量误差中绝对不含系统误差，它们应该是纯偶然误差(有固定的變異數)，围绕真值波动。除此之外，测量误差符合正态分布，这保证了偏差值在最后的结果y上忽略不计。

确定拟合的标准应该被重视，并小心选择，较大误差的测量值应被赋予较小的權。并建立如下规则：被选择的参数，应该使算出的函数曲线与观测值之差的平方和最小。用函数表示为：

$\min _{\vec {b}}{\sum _{i=1}^{n}(y_{m}-y_{i})^{2}}.$

用欧几里得度量表达为：

$\min _{\vec {b}}\|{\vec {y}}_{m}({\vec {b}})-{\vec {y}}\|_{2}^{2}\ .$

又因为$\|{\vec {y}}_{m}({\vec {b}})-{\vec {y}}\|_{2}$ ≥0,

所以也可以表示为$\min _{\vec {b}}\|{\vec {y}}_{m}({\vec {b}})-{\vec {y}}\|_{2}\ .$

最小化问题的精度，依赖于所选择的函数模型。

线性函数模型

典型的一类函数模型是线性函数模型。最简单的线性式是$y=b_{0}+b_{1}t$，写成矩陣式，为

$\min _{b_{0},b_{1}}\left\|{\begin{pmatrix}1&t_{1}\\\vdots &\vdots \\1&t_{n}\end{pmatrix}}{\begin{pmatrix}b_{0}\\b_{1}\end{pmatrix}}-{\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}\right\|_{2}=\min _{b}\|Ab-Y\|_{2}.$

直接给出该式的参数解：

$b_{1}={\frac {\sum _{i=1}^{n}t_{i}y_{i}-n\cdot {\bar {t}}{\bar {y}}}{\sum _{i=1}^{n}t_{i}^{2}-n\cdot ({\bar {t}})^{2}}}$ 和 $b_{0}={\bar {y}}-b_{1}{\bar {t}}$

其中${\bar {t}}={\frac {1}{n}}\sum _{i=1}^{n}t_{i}$，为t值的算术平均值。也可解得如下形式：

$b_{1}={\frac {\sum _{i=1}^{n}(t_{i}-{\bar {t}})(y_{i}-{\bar {y}})}{\sum _{i=1}^{n}(t_{i}-{\bar {t}})^{2}}}$

简单线性模型 y = b₀ + b₁t 的例子

随机选定10艘战舰，并分析它们的长度与宽度，寻找它们长度与宽度之间的关系。由下面的描点图可以直观地看出，一艘战舰的长度（t）与宽度（y）基本呈线性关系。散点图如下：

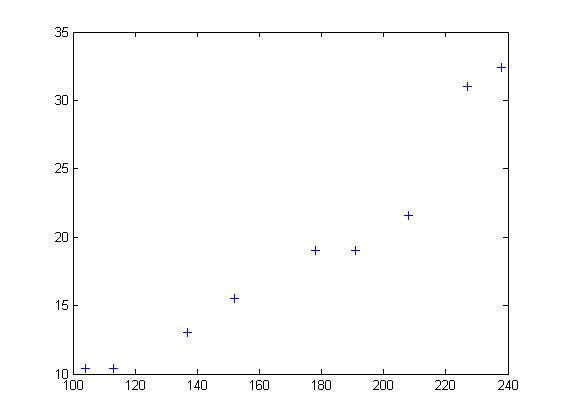
以下图表列出了各战舰的数据，随后步骤是采用最小二乘法确定两变量间的线性关系。

编号	长度 (m)	宽度 (m)	ti - t	yi - y
i	ti	yi	ti*	yi*	ti*yi*	ti*ti*	yi*yi*
1	208	21.6	40.2	3.19	128.238	1616.04	10.1761
2	152	15.5	-15.8	-2.91	45.978	249.64	8.4681
3	113	10.4	-54.8	-8.01	438.948	3003.04	64.1601
4	227	31.0	59.2	12.59	745.328	3504.64	158.5081
5	137	13.0	-30.8	-5.41	166.628	948.64	29.2681
6	238	32.4	70.2	13.99	982.098	4928.04	195.7201
7	178	19.0	10.2	0.59	6.018	104.04	0.3481
8	104	10.4	-63.8	-8.01	511.038	4070.44	64.1601
9	191	19.0	23.2	0.59	13.688	538.24	0.3481
10	130	11.8	-37.8	-6.61	249.858	1428.84	43.6921
总和（Σ）	1678	184.1	0.0	0.00	3287.820	20391.60	574.8490

仿照上面给出的例子

${\bar {t}}={\frac {\sum _{i=1}^{n}t_{i}}{n}}={\frac {1678}{10}}=167{.}8$ 并得到相应的${\bar {y}}=18{.}41$.

然后确定b₁

$b_{1}={\frac {\sum _{i=1}^{n}(t_{i}-{\bar {t}})(y_{i}-{\bar {y}})}{\sum _{i=1}^{n}(t_{i}-{\bar {t}})^{2}}}$

$={\frac {3287{.}820}{20391{.}60}}=0{.}1612\;,$

可以看出，战舰的长度每变化1m，相对应的宽度便要变化16cm。并由下式得到常数项b₀：

$b_{0}={\bar {y}}-b_{1}{\bar {t}}=18{.}41-0{.}1612\cdot 167{.}8=-8{.}6394\;,$

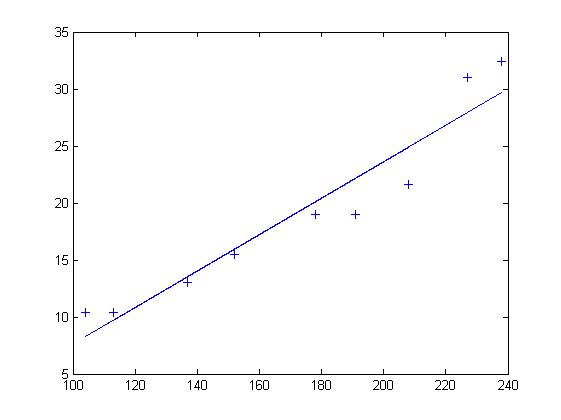
在这里随机理论不加阐述。可以看出点的拟合非常好，长度和宽度的相关性大约为96.03％。 利用Matlab得到拟合直线：

一般线性情况

若含有更多不相关模型变量$t_{1},...,t_{q}$，可如组成线性函数的形式

$y(t_{1},\dots ,t_{q};b_{0},b_{1},\dots ,b_{q})=b_{0}+b_{1}t_{1}+\cdots +b_{q}t_{q}$

即线性方程组

${\begin{matrix}b_{0}+b_{1}t_{11}+\cdots +b_{j}t_{1j}+\cdots +b_{q}t_{1q}=y_{1}\\b_{0}+b_{1}t_{21}+\cdots +b_{j}t_{2j}+\cdots +b_{q}t_{2q}=y_{2}\\\vdots \\b_{0}+b_{1}t_{i1}+\cdots +b_{j}t_{ij}+\cdots +b_{q}t_{iq}=y_{i}\\\vdots \\b_{0}+b_{1}t_{n1}+\cdots +b_{j}t_{nj}+\cdots +b_{q}t_{nq}=y_{n}\end{matrix}}$

通常人们将t_ij记作数据矩阵 A，参数b_j记做参数向量b，观测值y_i记作Y，则线性方程组又可写成：

${\begin{pmatrix}1&t_{11}&\cdots &t_{1j}\cdots &t_{1q}\\1&t_{21}&\cdots &t_{2j}\cdots &t_{2q}\\\vdots \\1&t_{i1}&\cdots &t_{ij}\cdots &t_{iq}\\\vdots \\1&t_{n1}&\cdots &t_{nj}\cdots &t_{nq}\end{pmatrix}}\cdot {\begin{pmatrix}b_{0}\\b_{1}\\b_{2}\\\vdots \\b_{j}\\\vdots \\b_{q}\end{pmatrix}}={\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{i}\\\vdots \\y_{n}\end{pmatrix}}$ 即 $Ab=Y$

上述方程运用最小二乘法导出为线性平方差计算的形式为：

$\min _{b}\|Ab-Y\|_{2}$。

最小二乘法的解

$\min _{b}\left\|{\boldsymbol {Ab}}-{\boldsymbol {Y}}\right\|_{2},{\boldsymbol {A}}\in \mathbf {C} ^{n\times m},{\boldsymbol {Y}}\in \mathbf {C} ^{n}$

的特解为A的广义逆矩阵与Y的乘积，这同时也是二范数极小的解，其通解为特解加上A的零空间。证明如下：

先将Y拆成A的值域及其正交补两部分

${\boldsymbol {Y}}={\boldsymbol {Y}}_{1}+{\boldsymbol {Y}}_{2}$

${\boldsymbol {Y}}_{1}={\boldsymbol {A}}{\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}\in R\left({\boldsymbol {A}}\right)$

${\boldsymbol {Y}}_{2}=\left({\boldsymbol {I}}-{\boldsymbol {A}}{\boldsymbol {A}}^{\dagger }\right){\boldsymbol {Y}}\in R\left({\boldsymbol {A}}\right)^{\bot }$

所以${\boldsymbol {Ab}}-{\boldsymbol {Y}}_{1}\in R\left({\boldsymbol {A}}\right)$，可得

$\left\|{\boldsymbol {Ab}}-{\boldsymbol {Y}}\right\|^{2}=\left\|{\boldsymbol {Ab}}-{\boldsymbol {Y}}_{1}+\left(-{\boldsymbol {Y}}_{2}\right)\right\|^{2}=\left\|{\boldsymbol {Ab}}-{\boldsymbol {Y}}_{1}\right\|^{2}+\left\|{\boldsymbol {Y}}_{2}\right\|^{2}$

故当且仅当${\boldsymbol {b}}$是${\boldsymbol {Ab}}={\boldsymbol {Y}}_{1}={\boldsymbol {A}}{\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}$解时，${\boldsymbol {b}}$即为最小二乘解，即${\boldsymbol {b}}={\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}={\left({{{\mathbf {A} }^{H}}{\mathbf {A} }}\right)^{-1}}{{\mathbf {A} }^{H}}{\mathbf {Y} }$。

又因为

$N\left({\boldsymbol {A}}\right)=N\left({\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right)=R\left({\boldsymbol {I}}-{\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right)=\left\{\left({\boldsymbol {I}}-{\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right){\boldsymbol {h}}:{\boldsymbol {h}}\in \mathbf {C} ^{n}\right\}$

故${\boldsymbol {Ab}}={\boldsymbol {A}}{\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}$的通解为

${\boldsymbol {b}}={\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}+\left({\boldsymbol {I}}-{\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right){\boldsymbol {h}}:{\boldsymbol {h}}\in \mathbf {C} ^{n}$

因为

${\begin{aligned}\left\|{\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}\right\|^{2}&<\left\|{\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}\right\|^{2}+\left\|\left({\boldsymbol {I}}-{\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right){\boldsymbol {h}}\right\|^{2}\\&=\left\|{\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}+\left({\boldsymbol {I}}-{\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right){\boldsymbol {h}}\right\|^{2},\left({\boldsymbol {I}}-{\boldsymbol {A}}^{\dagger }{\boldsymbol {A}}\right){\boldsymbol {h}}\neq {\boldsymbol {0}}\\\end{aligned}}$

所以${\boldsymbol {A}}^{\dagger }{\boldsymbol {Y}}$又是二范数极小的最小二乘解。

参考文献

书籍

• Wang Guorong; Wei Yimin; Qiao SanZheng. Equation Solving Generalized Inverses. Generalized Inverses: Theory and Computations. Beijing: Science Press. 2004: 6. ISBN 7-03-012437-5 （英语）. 
• Mansfield Merriman. "A List of Writings Relating to the Method of Least Squares". 

外部链接

• 3種統計學點估計的理論推演:動差法,最小平方法,最大概似估計法 （页面存档备份，存于互联网档案馆）
• http://www.physics.csbsju.edu/stats/least_squares.html （页面存档备份，存于互联网档案馆）
• https://web.archive.org/web/20200218162523/http://www.zunzun.com/
• http://www.orbitals.com/self/least/least.htm （页面存档备份，存于互联网档案馆）
• 最小二乘法. PlanetMath.