不连续点:修订间差异
外观
删除的内容 添加的内容
Symplectopedia(留言 | 贡献) 内容扩充 |
Ohtashinichiro(留言 | 贡献) |
||
| (未显示25个用户的40个中间版本) | |||
| 第1行: | 第1行: | ||
{{about|实变函数的不连续点的分类|复变函数的奇点的分类|奇点_(数学)}} |
|||
{{微积分学}} |
{{微积分学}} |
||
'''不连续点''',又称'''间断点''','''分段点'''({{lang-en|Discontinuities}}),通常是在單變數[[實变函數]]的環境下討論。令<math>E\subseteq \mathbb{R},~f:E\to\mathbb{R}</math>,且若<math>c\in\mathbb{R}</math>(不一定要在<math>E</math>中),若<math>f</math>在<math>c</math>不連續,則稱<math>f</math>在那裡有個不連續點、<math>c</math>為一個<math>f</math>的不連續點。 |
|||
'''间断点'''是指:在非[[连续]]函数y=f(x)中某点处x{{sub|o}}处有中断现象,那么,x{{sub|o}}就称为函数的间断点。 |
|||
==分类== |
== 分类 == |
||
根据不同 |
根据不同不连续点的性质,通常把不连续点分为两类: |
||
#第一类 |
#第一类不连续点: |
||
## |
##可去不连续点:不连续点两侧函数的极限存在且相等 。 |
||
## |
##跳跃不连续点:不连续点两侧函数的[[函數極限|极限]]存在,但不[[相等]]; |
||
#第二类 |
#第二类不连续点: |
||
:不属于第一类 |
:不属于第一类不连续点的任何一种不连续点都属于第二类不连续点。第二类不连续点可以进一步分为无穷不连续点和震荡不连续点。 |
||
==例子== |
== 例子 == |
||
[[ |
[[File:Discontinuity_removable.eps.png|thumb|right|可去不连续点]] |
||
1. 考虑以下函数: |
1. 考虑以下函数: |
||
:<math>f(x)=\begin{cases}x^2 & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ 2-x& \mbox{ for } x>1\end{cases}</math> |
:<math>f(x)=\begin{cases}x^2 & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ 2-x& \mbox{ for } x>1\end{cases}</math> |
||
点<math>x_0=1</math>是可去 |
点<math>x_0=1</math>是可去不连续点。 |
||
[[ |
[[File:Discontinuity_jump.eps.png|thumb|right|跳跃不连续点]] |
||
2. 考虑以下函数: |
2. 考虑以下函数: |
||
:<math>f(x)=\begin{cases}x^2 & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ 2-(x-1)^2& \mbox{ for } x>1\end{cases}</math> |
:<math>f(x)=\begin{cases}x^2 & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ 2-(x-1)^2& \mbox{ for } x>1\end{cases}</math> |
||
点<math>x_0=1</math>是跳跃 |
点<math>x_0=1</math>是跳跃不连续点。 |
||
[[ |
[[File:Discontinuity essential.svg|thumb|right|第二类不连续点]] |
||
3. 考虑以下函数: |
3. 考虑以下函数: |
||
:<math>f(x)=\begin{cases}\sin\frac{5}{x-1} & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ \frac{0.1}{x-1}& \mbox{ for } x>1\end{cases}</math> |
:<math>f(x)=\begin{cases}\sin\frac{5}{x-1} & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ \frac{0.1}{x-1}& \mbox{ for } x>1\end{cases}</math> |
||
点<math>x_0=1</math>是第二类 |
点<math>x_0=1</math>是第二类不连续点,又称本性不连续点。 |
||
== 外部链接 == |
|||
| ⚫ | |||
* {{Planetmath reference|title=Discontinuous|id=4447|urlname=discontinuous}} |
|||
* [http://demonstrations.wolfram.com/Discontinuity/ "Discontinuity"] {{Wayback|url=http://demonstrations.wolfram.com/Discontinuity/ |date=20220108040132 }} by Ed Pegg, Jr., The Wolfram Demonstrations Project, 2007. |
|||
* {{MathWorld | urlname=Discontinuity | title=Discontinuity}} |
|||
[[Category:连续映射]] |
|||
[[de:Sprungstetigkeit]] |
|||
| ⚫ | |||
[[en:Classification of discontinuities]] |
|||
[[es:Clasificación de discontinuidades]] |
|||
[[he:נקודת אי רציפות]] |
|||
[[it:Punto di discontinuità]] |
|||
[[ko:불연속성의 분류]] |
|||
[[nl:Discontinuïteit]] |
|||
[[sv:Diskontinuitet]] |
|||
2024年7月18日 (四) 03:20的最新版本
| 系列條目 |
| 微积分学 |
|---|
 |
不连续点,又称间断点,分段点(英語:Discontinuities),通常是在單變數實变函數的環境下討論。令,且若(不一定要在中),若在不連續,則稱在那裡有個不連續點、為一個的不連續點。
分类
[编辑]根据不同不连续点的性质,通常把不连续点分为两类:
- 不属于第一类不连续点的任何一种不连续点都属于第二类不连续点。第二类不连续点可以进一步分为无穷不连续点和震荡不连续点。
例子
[编辑]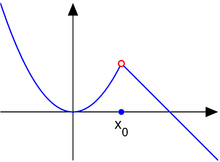
1. 考虑以下函数:
点是可去不连续点。
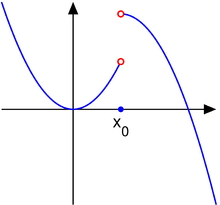
2. 考虑以下函数:
点是跳跃不连续点。

3. 考虑以下函数:
点是第二类不连续点,又称本性不连续点。
外部链接
[编辑]- Discontinuous. PlanetMath.
- "Discontinuity" (页面存档备份,存于互联网档案馆) by Ed Pegg, Jr., The Wolfram Demonstrations Project, 2007.
- 埃里克·韦斯坦因. Discontinuity. MathWorld.









