范数:修订间差异
外观
删除的内容 添加的内容
Kelly Hwong(留言 | 贡献) 小 →绝对值范数 |
Add 1 book for verifiability (20240907)) #IABot (v2.0.9.5) (GreenC bot |
||
| (未显示5个用户的8个中间版本) | |||
| 第1行: | 第1行: | ||
{{NoteTA|G1=math}} |
{{NoteTA|G1=math}} |
||
{{Not|範數 (域論)}} |
|||
[[File:Vector norms.svg|thumb|擁有不同範數的[[單位圓]]]] |
[[File:Vector norms.svg|thumb|擁有不同範數的[[單位圓]]]] |
||
'''範數'''({{lang-en| |
'''範數'''({{lang-en|Norm}}),是具有“长度”概念的[[函數]]。在[[線性代數]]、[[泛函分析]]及相關的數學領域,是一個[[函數]],其為[[向量空間]]內的所有[[向量]]賦予非零的正'''長度'''或'''大小'''。另一方面,'''半範數'''({{lang-en|seminorm}})可以為非零的[[向量]]賦予零長度。 |
||
舉一個簡單的例子,一個二維度的歐 |
舉一個簡單的例子,一個二維度的[[歐幾里得空間]]<math>\R^2</math>就有歐氏範數。在這個[[向量空間]]的元素(譬如:(3,7))常常在[[直角坐标系|笛卡兒座標系統]]被畫成一個從原點出發的箭號。每一個[[向量]]的歐氏範數就是箭號的長度。 |
||
擁有範數的[[向量空間]]就是[[賦範向量空間]]。同樣,擁有半範數的[[向量空間]]就是賦半範向量空間。 |
擁有範數的[[向量空間]]就是[[賦範向量空間]]。同樣,擁有半範數的[[向量空間]]就是賦半範向量空間。 |
||
| 第18行: | 第19行: | ||
:4. <math>p(v)=0</math>,当且仅当<math>v</math>是[[零向量]]([[正定性]]) |
:4. <math>p(v)=0</math>,当且仅当<math>v</math>是[[零向量]]([[正定性]]) |
||
如果拓撲向量空間的[[拓撲]]可以被範數導出,這個[[拓撲向量空間]]被稱為[[賦範向量空間]]。 |
如果拓撲向量空間的[[拓撲空間|拓撲]]可以被範數導出,這個[[拓撲向量空間]]被稱為[[賦範向量空間]]。 |
||
==例子== |
==例子== |
||
| 第24行: | 第25行: | ||
* 平凡半范数,即<math>p(x) = 0, \forall x \in V</math>。 |
* 平凡半范数,即<math>p(x) = 0, \forall x \in V</math>。 |
||
* [[绝对值]]是[[实数]]集上的一个范数。 |
* [[绝对值]]是[[实数]]集上的一个范数。 |
||
* 对向量空间上的[[ |
* 对向量空间上的[[Seminorm|次线性型]]''f''可定义一个半范数:<math>\boldsymbol x \to |f(\boldsymbol x)|</math>。 |
||
===绝对值范数=== |
===绝对值范数=== |
||
| 第53行: | 第54行: | ||
====复数的欧几里得范数==== |
====复数的欧几里得范数==== |
||
如果将[[复平面]]看作[[欧几里得平面]]<math>\mathbb R ^2</math>,那么[[复数]]的欧几里得范数是其[[复数 |
如果将[[复平面]]看作[[欧几里得平面]]<math>\mathbb R ^2</math>,那么[[复数 (数学)|复数]]的欧几里得范数是其[[复数 (数学)#絕對值、共軛與距離|绝对值]](又称为'''模''')。这样,我们可把<math>x+i\,y</math>视为欧几里得平面上的一个向量,由此,这个向量的欧几里得范数即为<math>\sqrt{x^2 +y^2}</math>(最初由欧拉提出)。 |
||
==參見== |
==參見== |
||
| 第68行: | 第69行: | ||
|last = Bourbaki |first = Nicolas |author-link = Nicolas Bourbaki |
|last = Bourbaki |first = Nicolas |author-link = Nicolas Bourbaki |
||
| title = Topological vector spaces |
| title = Topological vector spaces |
||
| year = 1987 |
|url = https://archive.org/details/topologicalvecto0000nbou | year = 1987 |
||
| chapter = Chapters 1–5 |
| chapter = Chapters 1–5 |
||
| publisher = [[Springer Science+Business Media|Springer]] |
| publisher = [[Springer Science+Business Media|Springer]] |
||
2024年9月8日 (日) 07:05的最新版本
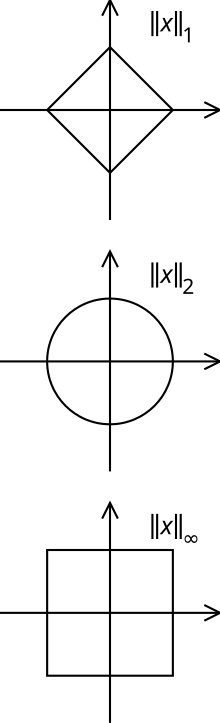
範數(英語:Norm),是具有“长度”概念的函數。在線性代數、泛函分析及相關的數學領域,是一個函數,其為向量空間內的所有向量賦予非零的正長度或大小。另一方面,半範數(英語:seminorm)可以為非零的向量賦予零長度。
舉一個簡單的例子,一個二維度的歐幾里得空間就有歐氏範數。在這個向量空間的元素(譬如:(3,7))常常在笛卡兒座標系統被畫成一個從原點出發的箭號。每一個向量的歐氏範數就是箭號的長度。
擁有範數的向量空間就是賦範向量空間。同樣,擁有半範數的向量空間就是賦半範向量空間。
定義
[编辑]假設V是域F上的向量空間;V的半範數是一個函數,满足:
,
範數是一個半範數加上額外性质:
如果拓撲向量空間的拓撲可以被範數導出,這個拓撲向量空間被稱為賦範向量空間。
例子
[编辑]绝对值范数
[编辑]绝对值范数為
是在由实数或虚数构成的一维向量空间中的范数。
绝对值范数是曼哈顿范数的特殊形式。
欧几里德范数
[编辑]在n维欧几里德空间上,向量的最符合直觉的长度由以下公式给出
根据勾股定理,它给出了从原点到点之间的(通常意义下的)距离。欧几里德范数是上最常用的范数,但正如下面举出的,上也可以定义其他的范数。然而,以下定义的范数都定义了同一个拓扑结构,因此它们在某种意义上都是等价的。
在一个n维复数空间中,最常见的范数是:
以上公式适用于任何内积空间,包括欧式空间和复空间。在欧几里得空间里,内积等价于点积,因此公式可以写成以下形式:
特别地,中所有的欧几里得范数为同一个给定正实数的向量的集合是一个n维球面。
复数的欧几里得范数
[编辑]如果将复平面看作欧几里得平面,那么复数的欧几里得范数是其绝对值(又称为模)。这样,我们可把视为欧几里得平面上的一个向量,由此,这个向量的欧几里得范数即为(最初由欧拉提出)。
參見
[编辑]參考文獻
[编辑]- Bourbaki, Nicolas. Chapters 1–5. Topological vector spaces. Springer. 1987. ISBN 3-540-13627-4.
- Prugovečki, Eduard. Quantum mechanics in Hilbert space 2nd. Academic Press. 1981: 20. ISBN 0-12-566060-X.
- Trèves, François. Topological Vector Spaces, Distributions and Kernels. Academic Press, Inc. 1995: 136–149, 195–201, 240–252, 335–390, 420–433. ISBN 0-486-45352-9.
- Khaleelulla, S. M. Counterexamples in Topological Vector Spaces. Lecture Notes in Mathematics 936. Springer-Verlag. 1982: 3–5. ISBN 978-3-540-11565-6. Zbl 0482.46002.



















![{\displaystyle [x_{1},x_{2},\,\ldots \,,x_{n}]^{\mathrm {T} }}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/6963dc3554a2f438e130cc49c7400fd216765a5a)




