(未显示16个用户的21个中间版本)
第1行:
第1行:
{{NoteTA
{{NoteTA
|T=zh-cn:叉积;zh-hant:外積;
| T = zh-cn:叉积;zh-hant:外積;
|G1 = Math
| G1 = Math|zh-hans:点积;zh-hant:內積;
}}
}}
{{dablink|“外積”重定向至此,關於常稱作'''外積'''的相關二元運算,参见[[外積 (消歧義)]]。}}
{{dablink|本文介绍 向量的向量积。 關於常稱作'''外積'''的相關二元運算,参见[[外积 ]]。}}
{{Linear algebra}}
{{Linear algebra}}
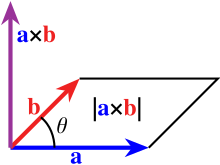
在[[数学]]和[[向量代数]]领域,'''外積'''({{lang-en|Cross product}})又称'''向量积'''({{lang-en|Vector product}}),是对[[三维空间]]中的两个[[向量]]的[[二元运算]],使用符号 <math>\times</math>。与[[点积]]不同,它的运算结果是[[向量]]。对于[[线性无关]]的两个向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math>,它们的外积写作 <math>\mathbf{a} \times \mathbf{b}</math>,是 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 所在平面的[[法线]]向量,与 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 都[[垂直]]。外积被广泛运用于数学、[[物理]]、[[工程学]]、[[计算机科学]]领域。
在[[数学]]和[[向量代数]]领域,'''外積'''({{lang-en|external product}})又称'''叉积'''({{lang|en|cross product}})、'''叉乘'''、 '''向量积'''({{lang| en|vector product}}),是对[[三维空间]]中的两个[[向量]]的[[二元运算]],使用符号<math>\times</math>。与[[点积]]不同,它的运算结果是[[向量]]。对于[[线性无关]]的两个向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>,它们的外积写作<math>\mathbf{a} \times \mathbf{b}</math>,是<math>\mathbf{a}</math>和<math>\mathbf{b}</math>所在平面的[[法线]]向量,与<math>\mathbf{a}</math>和<math>\mathbf{b}</math>都[[垂直]]。外积被广泛运用于数学、[[物理]]、[[工程学]]、[[计算机科学]]领域。
如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零。推广开来,外积的[[模长]]和以这两个向量为边的[[平行四边形]]的面积相等;如果两个向量成直角,它们外积的模长即为两者长度的乘积。
如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零。推广开来,外积的[[模长]]和以这两个向量为边的[[平行四边形]]的面积相等;如果两个向量成直角,它们外积的模长即为两者长度的乘积。
外积和[[点积]]一样依赖于[[欧几里德空间]]的[[度量空间|度量]],但与点积之不同的是,外积还依赖于[[定向_(向量空間)|定向]]或[[右手定則]]。
外积和[[点积]]一样依赖于[[欧几里德空间]]的[[度量空间|度量]],但与点积之不同的是,外积还依赖于[[定向_(向量空間)|定向]]或[[右手定則]]。
'''叉积'''的名称源自表示叉积运算的[[×|叉乘号]](<math>\mathbf a \times \mathbf b</math>),讀作<code>a cross b</code>,'''向量积'''的叫法则是在强调其运算结果为[[向量]]而非[[标量 (数学)|标量]]。向量的另一种乘法是'''[[点积]]'''(<math>\mathbf a \cdot \mathbf b</math>),讀作<code>a dot b</code>,其结果为[[标量 (数学)|标量]],称为'''[[点积]]'''或'''数量积'''或'''标量积'''。
[[Image:Cross product vector.svg|thumb|right|在右手坐标系中的向量积]]
[[Image:Cross product vector.svg|thumb|right|在右手坐标系中的向量积]]
第15行:
第17行:
== 定义 ==
== 定义 ==
[[File:Right hand rule cross product.svg|thumb|使用[[右手定則]]确定外积的方向]]
[[File:Right hand rule cross product.svg|thumb|使用[[右手定則]]确定外积的方向]]
两个向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 的外积仅在[[三维空间]]中有定义,写作 <math>\mathbf{a} \times \mathbf{b}</math>。在[[物理学]]中,外积有时也被写成<math>\mathbf{a} \wedge \mathbf{b}</math>,但在数学中 <math>\mathbf{a} \wedge \mathbf{b}</math> 是[[外代数]]中的外积。
两个向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>的外积仅在[[三维空间]]中有定义,写作<math>\mathbf{a} \times \mathbf{b}</math>。在[[物理学]]中,外积有时也被写成<math>\mathbf{a} \wedge \mathbf{b}</math>,但在数学中<math>\mathbf{a} \wedge \mathbf{b}</math>是[[外代数]]中的外积。
外积 <math>\mathbf{a} \times \mathbf{b}</math> 是与 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 都垂直的向量 <math>\mathbf{c}</math>。其方向由[[右手定則]]决定,[[模长]]等于以两个向量为边的[[平行四边形]]的面积。
外积<math>\mathbf{a} \times \mathbf{b}</math>是与<math>\mathbf{a}</math>和<math>\mathbf{b}</math>都垂直的向量<math>\mathbf{c}</math>。其方向由[[右手定則]]决定,[[范数 ]]等于以两个向量为边的[[平行四边形]]的[[ 面积]] 。
外积可以定义为:
外积可以定义为:
第23行:
第25行:
:<math>\mathbf{a} \times \mathbf{b} = \| \mathbf{a} \| \| \mathbf{b} \| \sin(\theta) \ \mathbf{n}</math>
:<math>\mathbf{a} \times \mathbf{b} = \| \mathbf{a} \| \| \mathbf{b} \| \sin(\theta) \ \mathbf{n}</math>
其中 <math>\theta</math> 表示 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 在它们所定义的平面上的[[角度|夹角]](<math>0^\circ \le \theta \le 180^\circ</math>)。<math>\| \mathbf{a} \|</math> 和 <math>\| \mathbf{b} \|</math> 是向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 的[[模长]],而 <math>\mathbf{n}</math> 则是一个与 <math>\mathbf{a}</math>、<math>\mathbf{b}</math> 所构成的平面[[垂直]]的[[单位向量]],方向由[[右手定則]]决定。根据上述公式,当 <math>\mathbf{a}</math> 与 <math>\mathbf{b}</math> 平行(即 <math>\theta</math> 为 0° 或 180°)时,它们的外积为[[零向量]] <math>\mathbf{0}</math>。
其中<math>\theta</math>表示<math>\mathbf{a}</math>和<math>\mathbf{b}</math>在它们所定义的平面上的[[角度|夹角]](<math>0^\circ \le \theta \le 180^\circ</math>)。<math>\| \mathbf{a} \|</math>和<math>\| \mathbf{b} \|</math>是向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>的[[模长]],而<math>\mathbf{n}</math>则是一个与<math>\mathbf{a}</math>、<math>\mathbf{b}</math>所构成的平面[[垂直]]的[[单位向量]],方向由[[右手定則]]决定。根据上述公式,当<math>\mathbf{a}</math>与<math>\mathbf{b}</math>平行(即<math>\theta</math>为0°或180°)时,它们的外积为[[零向量]]<math>\mathbf{0}</math>。
[[File:Cross product.gif|thumb|外积{{nowrap|'''a''' × '''b'''}}(垂直方向、紫色)随着向量 '''a'''(蓝色)和 '''b'''(红色)的夹角变化。 外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖'''a'''‖‖'''b'''‖。]]
[[File:Cross product.gif|thumb|外积{{nowrap|'''a''' × '''b'''}}(垂直方向、紫色)随着向量'''a'''(蓝色)和'''b'''(红色)的夹角变化。外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖'''a'''‖‖'''b'''‖。]]
按照惯例,向量 <math>\mathbf{n}</math> 的方向由[[右手定則]]决定:将右手[[食指]]指向 <math>\mathbf{a}</math> 的方向、[[中指]]指向 <math>\mathbf{b}</math> 的方向,则此时[[拇指]]的方向即为 <math>\mathbf{n}</math> 的方向。使用这一定则意味着外积满足[[反交换律]],<math>\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})</math>:将右手食指指向 <math>\mathbf{b}</math>、中指指向 <math>\mathbf{a}</math>,那么拇指就必定指向相反方向,即翻转了外积的符号。
按照惯例,向量<math>\mathbf{n}</math>的方向由[[右手定則]]决定:将右手[[食指]]指向<math>\mathbf{a}</math>的方向、[[中指]]指向<math>\mathbf{b}</math>的方向,则此时[[拇指]]的方向即为<math>\mathbf{n}</math>的方向。使用这一定则意味着外积满足[[反交换律]],<math>\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})</math>:将右手食指指向<math>\mathbf{b}</math>、中指指向<math>\mathbf{a}</math>,那么拇指就必定指向相反方向,即翻转了外积的符号。
由此可以看出,使用外积需要考虑坐标系的利手性({{lang-en|Handedness}}),如果使用的是[[笛卡尔坐标系#三維空間|左手坐标系]],向量 <math>\mathbf{n}</math> 的方向需要使用[[左手定则]]决定,与右手坐标系中的方向相反。
由此可以看出,使用外积需要考虑坐标系的利手性({{lang-en|Handedness}}),如果使用的是[[笛卡尔坐标系#三維空間|左手坐标系]],向量<math>\mathbf{n}</math>的方向需要使用[[左手定则]]决定,与右手坐标系中的方向相反。
这样就会带来一个问题:[[参照系]]的变换不应该影响 <math>\mathbf{n}</math> 的方向(例如从右手坐标系到左手坐标系的镜像变换)。因此,两个向量的外积并不是(真)向量,而是[[伪向量]]。
这样就会带来一个问题:[[参照系]]的变换不应该影响<math>\mathbf{n}</math>的方向(例如从右手坐标系到左手坐标系的镜像变换)。因此,两个向量的外积并不是(真)向量,而是[[贗 向量]]。
== 计算 ==
== 计算 ==
第37行:
第39行:
=== 坐标表示 ===
=== 坐标表示 ===
[[File:3D Vector.svg|300px|thumb|right|[[基向量]]('''i'''、'''j'''、'''k''',也记作 '''e'''<sub>1</sub>、'''e'''<sub>2</sub>、'''e'''<sub>3</sub>)和[[向量]] '''a''' 的分解('''a'''<sub>x</sub>、'''a'''<sub>y</sub>、'''a'''<sub>z</sub>,也记作 '''a'''<sub>1</sub>、'''a'''<sub>2</sub>、'''a'''<sub>3</sub>)]]
[[File:3D Vector.svg|300px|thumb|right|[[基向量]]('''i'''、'''j'''、'''k''',也记作'''e'''<sub>1</sub>、'''e'''<sub>2</sub>、'''e'''<sub>3</sub>)和[[向量]]'''a'''的分解('''a'''<sub>x</sub>、'''a'''<sub>y</sub>、'''a'''<sub>z</sub>,也记作'''a'''<sub>1</sub>、'''a'''<sub>2</sub>、'''a'''<sub>3</sub>)]]
右手坐标系中,[[基向量]] <math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math> 满足以下等式:
右手坐标系中,[[基向量]]<math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math>满足以下等式:
:<math>\begin{align}
:<math>\begin{align}
\mathbf{i}\times\mathbf{j} &= \mathbf{k}\\
\mathbf{i}\times\mathbf{j} &= \mathbf{k}\\
第58行:
第60行:
根据以上等式,结合外积的[[分配律]]和[[线性关系]],就可以确定任意向量的外积。
根据以上等式,结合外积的[[分配律]]和[[线性关系]],就可以确定任意向量的外积。
向量 <math>\mathbf{u}</math> 和 <math>\mathbf{v}</math> 可以定义为平行于[[基向量]]的三个正交元素之和:
向量<math>\mathbf{u}</math>和<math>\mathbf{v}</math>可以定义为平行于[[基向量]]的三个正交元素之和:
:<math>\begin{align}
:<math>\begin{align}
\mathbf{u} &= u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k} \\
\mathbf{u} &= u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k} \\
第64行:
第66行:
\end{align}</math>
\end{align}</math>
两者的外积 <math>\mathbf{u} \times \mathbf{v}</math> 可以根据[[分配律]]展开:
两者的外积<math>\mathbf{u} \times \mathbf{v}</math>可以根据[[分配律]]展开:
:<math> \begin{align}
:<math> \begin{align}
\mathbf{u}\times\mathbf{v} = {} &(u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k}) \times (v_1\mathbf{i} + v_2\mathbf{j} + v_3\mathbf{k})\\
\mathbf{u}\times\mathbf{v} = {} &(u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k}) \times (v_1\mathbf{i} + v_2\mathbf{j} + v_3\mathbf{k})\\
第72行:
第74行:
\end{align}</math>
\end{align}</math>
即把 <math>\mathbf{u} \times \mathbf{v}</math> 分解为九个仅涉及 <math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math> 的简单外积之和。九个外积各自所涉及的向量,要么相互平行、要么相互正交。将最前面所述的几个等式带入其中,然后合并同类项,可以得到:
即把<math>\mathbf{u} \times \mathbf{v}</math>分解为九个仅涉及<math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math>的简单外积之和。九个外积各自所涉及的向量,要么相互平行、要么相互正交。将最前面所述的几个等式带入其中,然后合并同类项,可以得到:
:<math>\begin{align}
:<math>\begin{align}
\mathbf{u}\times\mathbf{v} = {} &- u_1v_1\mathbf{0} + u_1v_2\mathbf{k} - u_1v_3\mathbf{j} \\
\mathbf{u}\times\mathbf{v} = {} &- u_1v_1\mathbf{0} + u_1v_2\mathbf{k} - u_1v_3\mathbf{j} \\
第80行:
第82行:
\end{align}</math>
\end{align}</math>
即结果向量 <math>\mathbf{s} = s_1\mathbf{i} + s_2\mathbf{j} + s_3\mathbf{k} = \mathbf{u} \times \mathbf{v} </math> 的三个[[标量]]元素为:
即结果向量<math>\mathbf{s} = s_1\mathbf{i} + s_2\mathbf{j} + s_3\mathbf{k} = \mathbf{u} \times \mathbf{v} </math>的三个[[标量 (数学)| 标量]]元素为:
:<math>\begin{align}
:<math>\begin{align}
s_1 &= u_2v_3-u_3v_2\\
s_1 &= u_2v_3-u_3v_2\\
第88行:
第90行:
也可以记作[[列向量]]的形式:
也可以记作[[列向量]]的形式:
:<math>\begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix}=\begin{pmatrix}u_2v_3-u_3v_2\\u_3v_1-u_1v_3\\u_1v_2-u_2v_1\end{pmatrix}</math>
:<math>\begin{pmatrix}s_1, s_2, s_3\end{pmatrix}=\begin{pmatrix}u_2v_3-u_3v_2, u_3v_1-u_1v_3, u_1v_2-u_2v_1\end{pmatrix}</math>
=== 矩阵表示 ===
=== 矩阵表示 ===
[[File:Sarrus rule cross product.svg|thumb|根据[[萨吕法则]]确定 '''u''' 和 '''v''' 的外积]]
[[File:Sarrus rule cross product.svg|thumb|根据[[萨吕法则]]确定'''u'''和'''v'''的外积]]
外积可以表达为这样的[[行列式]]:
外积可以表达为这样的[[行列式]]:
第99行:
第101行:
u_1&u_2&u_3\\
u_1&u_2&u_3\\
v_1&v_2&v_3\\
v_1&v_2&v_3\\
\end{vmatrix}</math><ref>{{cite book|author=[[鄭鈞 (物理學家)|David K. Cheng]]|title=''Field and Wave Electromagnetics''|year=2014|publisher=|isbn=9781292026565|pages=第21頁}}</ref>
\end{vmatrix}</math>
这个行列式可以使用[[萨吕法则]]或[[拉普拉斯展开]]计算。使用萨吕法则可以展开为:
这个行列式可以使用[[萨吕法则]]或[[拉普拉斯展开]]计算。使用萨吕法则可以展开为:
第107行:
第109行:
\end{align}</math>
\end{align}</math>
使用拉普拉斯展开可以沿第一行展开为:<ref name=Cullen2>{{cite book |title=''cited work'' |url=https://books.google.com/?id=x7uWk8lxVNYC&pg=PA321 |page=321 |chapter= Equation 7: '''a''' × '''b''' as sum of determinants |isbn=0-7637-4591-X |author1=Dennis G. Zill |author2=Michael R. Cullen |publisher=Jones & Bartlett Learning |year=2006}}</ref>
使用[[ 拉普拉斯展开]] 可以沿第一行展开为:<ref name=Cullen2>{{cite book |title=''cited work'' |url=https://books.google.com/?id=x7uWk8lxVNYC&pg=PA321 |page=321 |chapter= Equation 7: '''a''' × '''b''' as sum of determinants |isbn=0-7637-4591-X |author1=Dennis G. Zill |author2=Michael R. Cullen |publisher=Jones & Bartlett Learning |year=2006}}</ref>
:<math>\begin{align}
:<math>\begin{align}
\mathbf{u\times v} &=
\mathbf{u\times v} &=
第130行:
第132行:
===代数性质 ===
===代数性质 ===
對於任意三個向量 <math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math>,
對於任意三個向量<math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math>,
*<math>\mathbf{a} \times \mathbf{a} = \mathbf{0}</math>
*<math>\mathbf{a} \times \mathbf{a} = \mathbf{0}</math>
*<math>\mathbf{a} \times \mathbf{0} = \mathbf{0}</math>
*<math>\mathbf{a} \times \mathbf{0} = \mathbf{0}</math>
第144行:
第146行:
\end{vmatrix}</math>([[拉格朗日恆等式]])
\end{vmatrix}</math>([[拉格朗日恆等式]])
一般來說,向量外積不遵守[[約簡律]],即 <math>\mathbf{a} \times \mathbf{b} = \mathbf{a} \times \mathbf{c}</math> 不表示 <math>\mathbf{b} = \mathbf{c}</math>。此外,<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math> 不表示 <math>\mathbf{a} = \mathbf{0}</math> 或 <math>\mathbf{b} = \mathbf{0}</math>。
一般來說,向量外積不遵守[[約簡律]],即<math>\mathbf{a} \times \mathbf{b} = \mathbf{a} \times \mathbf{c}</math>不表示<math>\mathbf{b} = \mathbf{c}</math>。此外,<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math>不表示<math>\mathbf{a} = \mathbf{0}</math>或<math>\mathbf{b} = \mathbf{0}</math>。
但對於两个非零向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math>,
但對於两个非零向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>,
*<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math> [[當且僅當]] <math>\mathbf{a}</math> 平行於 <math>\mathbf{b}</math>
*<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math>[[當且僅當]] <math>\mathbf{a}</math>平行於<math>\mathbf{b}</math>
=== 几何意义 ===
=== 几何意义 ===
第154行:
第156行:
[[File:Parallelepiped volume.svg|right|thumb|240px|图2:三个向量定义平行六面体]]
[[File:Parallelepiped volume.svg|right|thumb|240px|图2:三个向量定义平行六面体]]
如果以向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 为边构成一个[[平行四边形]],那么这两个向量外积的[[模长]]与这个平行四边形的正[[面积]]相等(如图1):
如果以向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>为边构成一个[[平行四边形]],那么这两个向量外积的[[范数 ]]与这个平行四边形的正[[面积]]相等(如图1):
:<math> \left\| \mathbf{a} \times \mathbf{b} \right\| = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin \theta .</math>
:<math> \left\| \mathbf{a} \times \mathbf{b} \right\| = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin \theta .</math>
同时,如果以向量 <math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math> 为棱构成一个[[平行六面体]],那么这个平行六面体的[[体积]] <math>\mathbf{V}</math> 也可以通过外积和点积的组合得到,这种积称作[[三重积#标量三重积|标量三重积]](如图2):
同时,如果以向量<math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math>为棱构成一个[[平行六面体]],那么这个平行六面体的[[体积]]<math>\mathbf{V}</math>也可以通过外积和点积的组合得到,这种积称作[[三重积#标量三重积|标量三重积]](如图2):
:<math>
:<math>
\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=
\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=
第172行:
第174行:
===向量微分===
===向量微分===
對於實數 <math>t</math> 和兩個向量值函數 <math>\mathbf{a}(t)</math>、<math>\mathbf{b}(t)</math>,[[乘積法則]]成立:
對於實數<math>t</math>和兩個向量值函數<math>\mathbf{a}(t)</math>、<math>\mathbf{b}(t)</math>,[[乘積法則]]成立:
*<math>\frac{d}{dt}(\mathbf{a} \times \mathbf{b}) = \frac{d\mathbf{a}}{dt} \times \mathbf{b} + \mathbf{a} \times \frac{d\mathbf{b}}{dt}</math>
*<math>\frac{d}{dt}(\mathbf{a} \times \mathbf{b}) = \frac{d\mathbf{a}}{dt} \times \mathbf{b} + \mathbf{a} \times \frac{d\mathbf{b}}{dt}</math>
第197行:
第199行:
\end{align}</math>
\end{align}</math>
外积也可以用[[四元数]]来表示。注意到上述 <math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math> 之间的外积满足四元数的乘法。一般而言,若将向量[''a''<sub>1</sub>, ''a''<sub>2</sub>, ''a''<sub>3</sub>]表示成四元数''a''<sub>1</sub>''i'' + ''a''<sub>2</sub>''j'' + ''a''<sub>3</sub>''k'',两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见[[四元数与空间旋转]]。
外积也可以用[[四元数]]来表示。注意到上述<math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math>之间的外积满足四元数的乘法。一般而言,若将向量[''a''<sub>1</sub>, ''a''<sub>2</sub>, ''a''<sub>3</sub>]表示成四元数''a''<sub>1</sub>''i'' + ''a''<sub>2</sub>''j'' + ''a''<sub>3</sub>''k'',两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见[[四元数与空间旋转]]。
== 高维情形 ==
== 高维情形 ==
第210行:
第212行:
:<math>\mathbf{x} \times \mathbf{y} + \mathbf{y} \times \mathbf{x} = \mathbf{0}</math>
:<math>\mathbf{x} \times \mathbf{y} + \mathbf{y} \times \mathbf{x} = \mathbf{0}</math>
*<math>\mathbf{x} \times \mathbf{y}</math> 同时与 <math>\mathbf{x}</math> 和 <math>\mathbf{y}</math> 垂直:
*<math>\mathbf{x} \times \mathbf{y}</math>同时与<math>\mathbf{x}</math>和<math>\mathbf{y}</math>垂直:
:<math>\mathbf{x} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{y} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{0}</math>
:<math>\mathbf{x} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{y} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{0}</math>
第222行:
第224行:
另外,在物理学[[力学]]、[[电磁学]]、[[光学]]和[[计算机图形学]]等理工学科中,外积应用十分广泛。例如[[力矩]]、[[角动量]]、[[洛伦兹力]]等矢量都可以由向量的外积求解。在进行这些物理量的计算时,往往可以借助[[右手定则]]辅助判断方向。
另外,在物理学[[力学]]、[[电磁学]]、[[光学]]和[[计算机图形学]]等理工学科中,外积应用十分广泛。例如[[力矩]]、[[角动量]]、[[洛伦兹力]]等矢量都可以由向量的外积求解。在进行这些物理量的计算时,往往可以借助[[右手定则]]辅助判断方向。
== 历史 ==
== 历史 ==
{{Rough translation|||章節|time=2021-06-09}}
在1773年,[[约瑟夫·拉格朗日]]介绍了点积和叉积的概念来学习三维空间中的[[四面体]]。在1843年,[[威廉·哈密顿]]介绍了四元数乘积,并使用了术语“向量”和“标量”。给定两个四元数[0,'''u''']和[0,'''v'''],其中u和v是<math>R^3</math>空间中的向量,它们四元数乘积可以被总结为<math>[-\mathbf{u} \cdot \mathbf{v},\mathbf{u}\times\mathbf{v}]</math>。[[詹姆斯·克拉克·麦克斯韦]]使用了[[威廉·哈密顿]]的四元数工具发展了著名的[[麦克斯韦方程组]],因为各种原因,四元数在很长的一段时间内是物理教育中一个必要的部分。<br>
1773年,[[约瑟夫·拉格朗日]]引入 了点积和叉积的概念来研究 三维空间中的[[四面体]]。1843年,[[威廉·哈密顿]]引入 了四元数乘法 ,同时区分 了“向(矢) 量”和“标量”的概念 。给定两个四元数[0,'''u''']和[0,'''v'''],其中u和v是<math>R^3</math>空间中的向量,使得其 乘积可以写成 为<math>[-\mathbf{u} \cdot \mathbf{v},\mathbf{u}\times\mathbf{v}]</math>的形式 。[[詹姆斯·克拉克·麦克斯韦]]在 四元数的基础建立 了著名的[[麦克斯韦方程组]]。四元数因此(同时也 因为其他方面的)应用 ,在很长一段时间内都 是物理学 教育的 必备内容 。
⚫ 在1878年[[威廉·金顿·克利福德]]发表
了他的《
[[Elements of Dynamic
]]》
,这在当时是很先进的文本。他定义了两个向量的叉积
在大小上等于以这两个向量为边的平行四边形的面积,方向上垂直于它们的平面。
<br>
⚫ [[奥利弗·亥维赛]]和[[乔赛亚·威拉德·吉布斯]]都
觉得四元数方法太麻烦,通常需要提取结果中的标量和矢量部分。
因此在四元数乘
积被引入
的四十年后,点积和叉积
也同样被引入-以
激烈反对。
(最终)接受的关键是新方法
的效率,使得[[亥维赛]]可以将麦克斯韦方程组由最初的20个减为今天常见的4个。
<br>
⚫ 在1878年[[威廉·金顿·克利福德]]
在 发表的《
{{link-en| Elements of Dynamic
}} 》
中将 两个向量的叉积
的范数定义为 以这两个向量为边的平行四边形的面积,
且在在 方向上垂直于它们
所确定 的平面。
⚫ 在很大程度上独立于这种发展,而且当时基本上不受欢迎,[[赫尔曼·格拉斯曼]]发明了一种
几何代数,与二维和三维空间无关,在其中
外积起着中心作用。在1853年,[[奥古斯丁·路易·柯西]]
,与Grassmann同时代的人,在algebraic keys上发表了一篇文章
,用于求解方程,
并且和叉积有着相同的乘法特性。
Clifford将
Hamilton和
Grassmann的代数结合起来创建了[[克利福德代数]]
,在三维矢量的情况下,由两个矢量产生的双向量二重化为一个矢量,从而产生叉积。
<br>
⚫ 交叉符号和“叉积”这个名字是从
Gibbs开始的,它们最初出现在1881年给他的学生的私人出版笔记中,叫做《向量分析的元素》。
[[Aleksandr Kotelnikov]]指出了它在力学中的实用性。Gibbs的符号
和“叉乘”这个名字后来通过他以前的学生
[[Edwin Bidwell Wilson
]]编写的
一本《向量分析》(
[[Vector Analysis
]])
教科书获得了广泛的读者。
Wilson从
Gibbs的课件中重新组织了材料,以及
Heaviside,Föpps和Hamilton出版的材料。他把向量分析分为下列三个部分:
<br>
⚫ 四元数方法通常需要提取结果中的标量和矢量部分的信息,因此 [[奥利弗·亥维赛]]和[[乔赛亚·威拉德·吉布斯]]都
认为其过于冗长 。
于是 在四元数乘
法 被引入
约 四十年后,
他们在激烈的反对声中引入了 点积和叉积以
作为替代方案 。新方法
在 效率
上的便捷最终得到了一致认可 ,使得[[亥维赛]]可以将麦克斯韦方程组由最初的20个减为今天常见的4个。
⚫ 在很大程度上独立于这种发展,而且当时基本上不受欢迎,[[赫尔曼·格拉斯曼]]发明了一种与二维和三维空间无关
几何代数 ,
外积 在其中起着中心作用。在1853年,
与格拉斯曼同时代的人 [[奥古斯丁·路易·柯西]]发表了一篇
关于代数键的 文章
。代数键可 用于求解方程,且和叉积有着相同的乘法特性。
克利福德 将
哈密顿 和
格拉斯曼 的代数结合起来
, 创建了[[克利福德代数]]
。 在三维矢量的情况下,由两个矢量产生的双向量二重化为一个矢量,从而产生叉积。
⚫ 交叉符号和“叉积”这个名字是从
[[乔赛亚·威拉德·吉布斯]] 开始的,它们最初出现在1881年给他的学生的私人出版笔记中,叫做《向量分析的元素》。
吉布斯 的符号
以及 “叉乘”这个名字后来通过他以前的学生
{{link-en|埃德温·B·威尔逊| Edwin Bidwell Wilson
}} 编写的
教科书 《向量分析》(
{{link-en| Vector Analysis
}} )获得了广泛的读者。
威尔逊 从
吉布斯 的课件中重新组织了材料,以及
Heaviside,Föpps 和Hamilton出版的材料。他把向量分析分为下列三个部分:
{{quote|第一,关于向量的加法和标量与向量的乘积。第二,关于微分和积分与标量函数和向量函数的关系。第三,包含了线性向量函数的理论。}}
{{quote|第一,关于向量的加法和标量与向量的乘积。第二,关于微分和积分与标量函数和向量函数的关系。第三,包含了线性向量函数的理论。}}
定义了两个主要的向量乘法,称为:
定义了两个主要的向量乘法,称为:
* 两个向量的'''直接乘''','''标量乘'''或者'''点乘'''。
* 两个向量的'''直接乘''','''标量乘'''或者'''点乘'''。
* 两个向量的'''斜乘''','''向量乘'''或'''叉乘'''。<br>
* 两个向量的'''斜乘''','''向量乘'''或'''叉乘'''。
还研究了几种三重积和三重以上向量的乘积。还包括上述的三重积扩展。
还研究了几种三重积和三重以上向量的乘积。还包括上述的三重积扩展。
第238行:
第248行:
* [[右手定则]]
* [[右手定则]]
* [[外代数]]:外乘的实质,赝矢量与赝标量
* [[外代数]]:外乘的实质,赝矢量与赝标量
== 参考文献 ==
{{Reflist}}
[[Category:向量]]
[[Category:向量]]
本文介绍向量的向量积。關於常稱作
外積 的相關二元運算,参见
外积 。
线性代数
A
=
[
1
2
3
4
]
{\displaystyle \mathbf {A} ={\begin{bmatrix}1&2\\3&4\end{bmatrix}}}
向量 · 向量空间 · 基底 · 行列式 · 矩阵
在数学 和向量代数 领域,外積 (英語:external product )又称叉积 (cross product )、叉乘 、向量积 (vector product ),是对三维空间 中的两个向量 的二元运算 ,使用符号
×
{\displaystyle \times }
点积 不同,它的运算结果是向量 。对于线性无关 的两个向量
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
法线 向量,与
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
垂直 。外积被广泛运用于数学、物理 、工程学 、计算机科学 领域。
如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零。推广开来,外积的模长 和以这两个向量为边的平行四边形 的面积相等;如果两个向量成直角,它们外积的模长即为两者长度的乘积。
外积和点积 一样依赖于欧几里德空间 的度量 ,但与点积之不同的是,外积还依赖于定向 或右手定則 。
叉积 的名称源自表示叉积运算的叉乘号 (
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
a cross b,向量积 的叫法则是在强调其运算结果为向量 而非标量 。向量的另一种乘法是点积
a
⋅
b
{\displaystyle \mathbf {a} \cdot \mathbf {b} }
a dot b,其结果为标量 ,称为点积 数量积 或标量积 。
在右手坐标系中的向量积 使用右手定則 确定外积的方向 两个向量
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
三维空间 中有定义,写作
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
物理学 中,外积有时也被写成
a
∧
b
{\displaystyle \mathbf {a} \wedge \mathbf {b} }
a
∧
b
{\displaystyle \mathbf {a} \wedge \mathbf {b} }
外代数 中的外积。
外积
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
c
{\displaystyle \mathbf {c} }
右手定則 决定,范数 等于以两个向量为边的平行四边形 的面积 。
外积可以定义为:
a
×
b
=
‖
a
‖
‖
b
‖
sin
(
θ
)
n
{\displaystyle \mathbf {a} \times \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\sin(\theta )\ \mathbf {n} }
其中
θ
{\displaystyle \theta }
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
夹角 (
0
∘
≤
θ
≤
180
∘
{\displaystyle 0^{\circ }\leq \theta \leq 180^{\circ }}
‖
a
‖
{\displaystyle \|\mathbf {a} \|}
‖
b
‖
{\displaystyle \|\mathbf {b} \|}
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
模长 ,而
n
{\displaystyle \mathbf {n} }
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
垂直 的单位向量 ,方向由右手定則 决定。根据上述公式,当
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
θ
{\displaystyle \theta }
零向量
0
{\displaystyle \mathbf {0} }
外积a × b a (蓝色)和b (红色)的夹角变化。外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖a ‖‖b ‖。 按照惯例,向量
n
{\displaystyle \mathbf {n} }
右手定則 决定:将右手食指 指向
a
{\displaystyle \mathbf {a} }
中指 指向
b
{\displaystyle \mathbf {b} }
拇指 的方向即为
n
{\displaystyle \mathbf {n} }
反交换律 ,
a
×
b
=
−
(
b
×
a
)
{\displaystyle \mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} )}
b
{\displaystyle \mathbf {b} }
a
{\displaystyle \mathbf {a} }
由此可以看出,使用外积需要考虑坐标系的利手性(英語:Handedness ),如果使用的是左手坐标系 ,向量
n
{\displaystyle \mathbf {n} }
左手定则 决定,与右手坐标系中的方向相反。
这样就会带来一个问题:参照系 的变换不应该影响
n
{\displaystyle \mathbf {n} }
贗向量 。
基向量 (i 、j 、k ,也记作e 1 、e 2 、e 3 )和向量 a 的分解(a x 、a y 、a z ,也记作a 1 、a 2 、a 3 )右手坐标系中,基向量
i
{\displaystyle \mathbf {i} }
j
{\displaystyle \mathbf {j} }
k
{\displaystyle \mathbf {k} }
i
×
j
=
k
j
×
k
=
i
k
×
i
=
j
{\displaystyle {\begin{aligned}\mathbf {i} \times \mathbf {j} &=\mathbf {k} \\\mathbf {j} \times \mathbf {k} &=\mathbf {i} \\\mathbf {k} \times \mathbf {i} &=\mathbf {j} \end{aligned}}}
根据反交换律 可以得出:
j
×
i
=
−
k
k
×
j
=
−
i
i
×
k
=
−
j
{\displaystyle {\begin{aligned}\mathbf {j\times i} &=-\mathbf {k} \\\mathbf {k\times j} &=-\mathbf {i} \\\mathbf {i\times k} &=-\mathbf {j} \end{aligned}}}
根据外积的定义可以得出:
i
×
i
=
j
×
j
=
k
×
k
=
0
{\displaystyle \mathbf {i} \times \mathbf {i} =\mathbf {j} \times \mathbf {j} =\mathbf {k} \times \mathbf {k} =\mathbf {0} }
零向量 )。根据以上等式,结合外积的分配律 和线性关系 ,就可以确定任意向量的外积。
向量
u
{\displaystyle \mathbf {u} }
v
{\displaystyle \mathbf {v} }
基向量 的三个正交元素之和:
u
=
u
1
i
+
u
2
j
+
u
3
k
v
=
v
1
i
+
v
2
j
+
v
3
k
{\displaystyle {\begin{aligned}\mathbf {u} &=u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} \\\mathbf {v} &=v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} \end{aligned}}}
两者的外积
u
×
v
{\displaystyle \mathbf {u} \times \mathbf {v} }
分配律 展开:
u
×
v
=
(
u
1
i
+
u
2
j
+
u
3
k
)
×
(
v
1
i
+
v
2
j
+
v
3
k
)
=
u
1
v
1
(
i
×
i
)
+
u
1
v
2
(
i
×
j
)
+
u
1
v
3
(
i
×
k
)
+
u
2
v
1
(
j
×
i
)
+
u
2
v
2
(
j
×
j
)
+
u
2
v
3
(
j
×
k
)
+
u
3
v
1
(
k
×
i
)
+
u
3
v
2
(
k
×
j
)
+
u
3
v
3
(
k
×
k
)
{\displaystyle {\begin{aligned}\mathbf {u} \times \mathbf {v} ={}&(u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} )\times (v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} )\\={}&u_{1}v_{1}(\mathbf {i} \times \mathbf {i} )+u_{1}v_{2}(\mathbf {i} \times \mathbf {j} )+u_{1}v_{3}(\mathbf {i} \times \mathbf {k} )+{}\\&u_{2}v_{1}(\mathbf {j} \times \mathbf {i} )+u_{2}v_{2}(\mathbf {j} \times \mathbf {j} )+u_{2}v_{3}(\mathbf {j} \times \mathbf {k} )+{}\\&u_{3}v_{1}(\mathbf {k} \times \mathbf {i} )+u_{3}v_{2}(\mathbf {k} \times \mathbf {j} )+u_{3}v_{3}(\mathbf {k} \times \mathbf {k} )\\\end{aligned}}}
即把
u
×
v
{\displaystyle \mathbf {u} \times \mathbf {v} }
i
{\displaystyle \mathbf {i} }
j
{\displaystyle \mathbf {j} }
k
{\displaystyle \mathbf {k} }
u
×
v
=
−
u
1
v
1
0
+
u
1
v
2
k
−
u
1
v
3
j
−
u
2
v
1
k
−
u
2
v
2
0
+
u
2
v
3
i
+
u
3
v
1
j
−
u
3
v
2
i
−
u
3
v
3
0
=
(
u
2
v
3
−
u
3
v
2
)
i
+
(
u
3
v
1
−
u
1
v
3
)
j
+
(
u
1
v
2
−
u
2
v
1
)
k
{\displaystyle {\begin{aligned}\mathbf {u} \times \mathbf {v} ={}&-u_{1}v_{1}\mathbf {0} +u_{1}v_{2}\mathbf {k} -u_{1}v_{3}\mathbf {j} \\&-u_{2}v_{1}\mathbf {k} -u_{2}v_{2}\mathbf {0} +u_{2}v_{3}\mathbf {i} \\&+u_{3}v_{1}\mathbf {j} -u_{3}v_{2}\mathbf {i} -u_{3}v_{3}\mathbf {0} \\={}&(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \\\end{aligned}}}
即结果向量
s
=
s
1
i
+
s
2
j
+
s
3
k
=
u
×
v
{\displaystyle \mathbf {s} =s_{1}\mathbf {i} +s_{2}\mathbf {j} +s_{3}\mathbf {k} =\mathbf {u} \times \mathbf {v} }
标量 元素为:
s
1
=
u
2
v
3
−
u
3
v
2
s
2
=
u
3
v
1
−
u
1
v
3
s
3
=
u
1
v
2
−
u
2
v
1
{\displaystyle {\begin{aligned}s_{1}&=u_{2}v_{3}-u_{3}v_{2}\\s_{2}&=u_{3}v_{1}-u_{1}v_{3}\\s_{3}&=u_{1}v_{2}-u_{2}v_{1}\end{aligned}}}
也可以记作列向量 的形式:
(
s
1
,
s
2
,
s
3
)
=
(
u
2
v
3
−
u
3
v
2
,
u
3
v
1
−
u
1
v
3
,
u
1
v
2
−
u
2
v
1
)
{\displaystyle {\begin{pmatrix}s_{1},s_{2},s_{3}\end{pmatrix}}={\begin{pmatrix}u_{2}v_{3}-u_{3}v_{2},u_{3}v_{1}-u_{1}v_{3},u_{1}v_{2}-u_{2}v_{1}\end{pmatrix}}}
根据萨吕法则 确定u 和v 的外积 外积可以表达为这样的行列式 :
u
×
v
=
|
i
j
k
u
1
u
2
u
3
v
1
v
2
v
3
|
{\displaystyle \mathbf {u\times v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\\end{vmatrix}}}
[ 1] 这个行列式可以使用萨吕法则 或拉普拉斯展开 计算。使用萨吕法则可以展开为:
u
×
v
=
(
u
2
v
3
i
+
u
3
v
1
j
+
u
1
v
2
k
)
−
(
u
3
v
2
i
+
u
1
v
3
j
+
u
2
v
1
k
)
=
(
u
2
v
3
−
u
3
v
2
)
i
+
(
u
3
v
1
−
u
1
v
3
)
j
+
(
u
1
v
2
−
u
2
v
1
)
k
{\displaystyle {\begin{aligned}\mathbf {u\times v} &=(u_{2}v_{3}\mathbf {i} +u_{3}v_{1}\mathbf {j} +u_{1}v_{2}\mathbf {k} )-(u_{3}v_{2}\mathbf {i} +u_{1}v_{3}\mathbf {j} +u_{2}v_{1}\mathbf {k} )\\&=(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}}
使用拉普拉斯展开 可以沿第一行展开为:[ 2]
u
×
v
=
|
u
2
u
3
v
2
v
3
|
i
−
|
u
1
u
3
v
1
v
3
|
j
+
|
u
1
u
2
v
1
v
2
|
k
=
(
u
2
v
3
−
u
3
v
2
)
i
−
(
u
1
v
3
−
u
3
v
1
)
j
+
(
u
1
v
2
−
u
2
v
1
)
k
{\displaystyle {\begin{aligned}\mathbf {u\times v} &={\begin{vmatrix}u_{2}&u_{3}\\v_{2}&v_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}u_{1}&u_{3}\\v_{1}&v_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}u_{1}&u_{2}\\v_{1}&v_{2}\end{vmatrix}}\mathbf {k} \\&=(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} -(u_{1}v_{3}-u_{3}v_{1})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \end{aligned}}}
都可以直接得到结果向量。
對於任意三個向量
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
c
{\displaystyle \mathbf {c} }
a
×
a
=
0
{\displaystyle \mathbf {a} \times \mathbf {a} =\mathbf {0} }
a
×
0
=
0
{\displaystyle \mathbf {a} \times \mathbf {0} =\mathbf {0} }
a
×
b
=
−
b
×
a
{\displaystyle \mathbf {a} \times \mathbf {b} =-\mathbf {b} \times \mathbf {a} }
反交换律 )
a
×
(
b
+
c
)
=
a
×
b
+
a
×
c
{\displaystyle \mathbf {a} \times (\mathbf {b} +\mathbf {c} )=\mathbf {a} \times \mathbf {b} +\mathbf {a} \times \mathbf {c} }
分配律 )
(
a
+
b
)
×
c
=
a
×
c
+
b
×
c
{\displaystyle (\mathbf {a} +\mathbf {b} )\times \mathbf {c} =\mathbf {a} \times \mathbf {c} +\mathbf {b} \times \mathbf {c} }
分配律 )
(
λ
a
)
×
b
=
λ
(
a
×
b
)
=
a
×
(
λ
b
)
{\displaystyle (\lambda \mathbf {a} )\times \mathbf {b} =\lambda (\mathbf {a} \times \mathbf {b} )=\mathbf {a} \times (\lambda \mathbf {b} )}
a
×
b
+
c
×
d
=
(
a
−
c
)
×
(
b
−
d
)
+
a
×
d
+
c
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} }
|
a
×
b
|
=
|
b
×
a
|
{\displaystyle |\mathbf {a} \times \mathbf {b} |=|\mathbf {b} \times \mathbf {a} |}
|
a
×
b
|
2
=
|
a
|
2
|
b
|
2
−
(
a
⋅
b
)
2
=
|
a
⋅
a
a
⋅
b
a
⋅
b
b
⋅
b
|
{\displaystyle |\mathbf {a} \times \mathbf {b} |^{2}=|\mathbf {a} |^{2}|\mathbf {b} |^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}={\begin{vmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{vmatrix}}}
拉格朗日恆等式 )一般來說,向量外積不遵守約簡律 ,即
a
×
b
=
a
×
c
{\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {a} \times \mathbf {c} }
b
=
c
{\displaystyle \mathbf {b} =\mathbf {c} }
a
×
b
=
0
{\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {0} }
a
=
0
{\displaystyle \mathbf {a} =\mathbf {0} }
b
=
0
{\displaystyle \mathbf {b} =\mathbf {0} }
但對於两个非零向量
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
a
×
b
=
0
{\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {0} }
當且僅當
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
图1:平行四边形面积即外积的模长 图2:三个向量定义平行六面体 如果以向量
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
平行四边形 ,那么这两个向量外积的范数 与这个平行四边形的正面积 相等(如图1):
‖
a
×
b
‖
=
‖
a
‖
‖
b
‖
sin
θ
.
{\displaystyle \left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\sin \theta .}
同时,如果以向量
a
{\displaystyle \mathbf {a} }
b
{\displaystyle \mathbf {b} }
c
{\displaystyle \mathbf {c} }
平行六面体 ,那么这个平行六面体的体积
V
{\displaystyle \mathbf {V} }
标量三重积 (如图2):
a
⋅
(
b
×
c
)
=
b
⋅
(
c
×
a
)
=
c
⋅
(
a
×
b
)
.
{\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).}
因为标量三重积可能为负,平行六面体的体积需要取其绝对值:
V
=
|
a
⋅
(
b
×
c
)
|
{\displaystyle V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}
因为外积的模长与其参数夹角的正弦有关,可以认为外积是「垂直度」的度量,正如点积 是「平行度」的度量一样。对于任意两个单位向量 ,外积为1意味着它们互相垂直,外积为0意味着它们互相平行。点积则相反:点积为0意味着它们互相垂直。
单位向量还能带来两个特性:两个单位向量的点积是它们夹角的余弦(可正可负);它们外积的模长则为夹角的正弦(始终为正)。
對於實數
t
{\displaystyle t}
a
(
t
)
{\displaystyle \mathbf {a} (t)}
b
(
t
)
{\displaystyle \mathbf {b} (t)}
乘積法則 成立:
d
d
t
(
a
×
b
)
=
d
a
d
t
×
b
+
a
×
d
b
d
t
{\displaystyle {\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}}}
给定直角坐标系的单位向量
i
{\displaystyle \mathbf {i} }
j
{\displaystyle \mathbf {j} }
k
{\displaystyle \mathbf {k} }
i
×
j
=
k
{\displaystyle \mathbf {i} \times \mathbf {j} =\mathbf {k} }
j
×
k
=
i
{\displaystyle \mathbf {j} \times \mathbf {k} =\mathbf {i} }
k
×
i
=
j
{\displaystyle \mathbf {k} \times \mathbf {i} =\mathbf {j} }
通过这些规则,两个向量的外积的坐标可以方便地计算出来,不需要考虑任何角度:设
a
=
a
1
i
+
a
2
j
+
a
3
k
{\displaystyle \mathbf {a} =a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k} }
b
=
b
1
i
+
b
2
j
+
b
3
k
{\displaystyle \mathbf {b} =b_{1}\mathbf {i} +b_{2}\mathbf {j} +b_{3}\mathbf {k} }
则
a
×
b
=
(
a
2
b
3
−
a
3
b
2
)
i
+
(
a
3
b
1
−
a
1
b
3
)
j
+
(
a
1
b
2
−
a
2
b
1
)
k
=
|
i
j
k
a
1
a
2
a
3
b
1
b
2
b
3
|
{\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} \\&={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}\end{aligned}}}
外积也可以用四元数 来表示。注意到上述
i
{\displaystyle \mathbf {i} }
j
{\displaystyle \mathbf {j} }
k
{\displaystyle \mathbf {k} }
a 1 , a 2 , a 3 ]表示成四元数a 1 i + a 2 j + a 3 k ,两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转 。
七维向量的外积可以通过八元数 得到,与上述的四元数方法相同。
七维外积具有与三维外积相似的性质:
x
×
(
a
y
+
b
z
)
=
a
x
×
y
+
b
x
×
z
{\displaystyle \mathbf {x} \times (a\mathbf {y} +b\mathbf {z} )=a\mathbf {x} \times \mathbf {y} +b\mathbf {x} \times \mathbf {z} }
(
a
y
+
b
z
)
×
x
=
a
y
×
x
+
b
z
×
x
{\displaystyle (a\mathbf {y} +b\mathbf {z} )\times \mathbf {x} =a\mathbf {y} \times \mathbf {x} +b\mathbf {z} \times \mathbf {x} }
x
×
y
+
y
×
x
=
0
{\displaystyle \mathbf {x} \times \mathbf {y} +\mathbf {y} \times \mathbf {x} =\mathbf {0} }
x
×
y
{\displaystyle \mathbf {x} \times \mathbf {y} }
x
{\displaystyle \mathbf {x} }
y
{\displaystyle \mathbf {y} }
x
⋅
(
x
×
y
)
=
y
⋅
(
x
×
y
)
=
0
{\displaystyle \mathbf {x} \cdot (\mathbf {x} \times \mathbf {y} )=\mathbf {y} \cdot (\mathbf {x} \times \mathbf {y} )=\mathbf {0} }
|
x
×
y
|
2
=
|
x
|
2
|
y
|
2
−
(
x
⋅
y
)
2
{\displaystyle |\mathbf {x} \times \mathbf {y} |^{2}=|\mathbf {x} |^{2}|\mathbf {y} |^{2}-(\mathbf {x} \cdot \mathbf {y} )^{2}}
x
×
(
y
×
z
)
+
y
×
(
z
×
x
)
+
z
×
(
x
×
y
)
≠
0
{\displaystyle \mathbf {x} \times (\mathbf {y} \times \mathbf {z} )\;+\mathbf {y} \times (\mathbf {z} \times \mathbf {x} )\;+\mathbf {z} \times (\mathbf {x} \times \mathbf {y} )\neq \mathbf {0} }
另外,在物理学力学 、电磁学 、光学 和计算机图形学 等理工学科中,外积应用十分广泛。例如力矩 、角动量 、洛伦兹力 等矢量都可以由向量的外积求解。在进行这些物理量的计算时,往往可以借助右手定则 辅助判断方向。
1773年,约瑟夫·拉格朗日 引入了点积和叉积的概念来研究三维空间中的四面体 。1843年,威廉·哈密顿 引入了四元数乘法,同时区分了“向(矢)量”和“标量”的概念。给定两个四元数[0,u ]和[0,v ],其中u和v是
R
3
{\displaystyle R^{3}}
[
−
u
⋅
v
,
u
×
v
]
{\displaystyle [-\mathbf {u} \cdot \mathbf {v} ,\mathbf {u} \times \mathbf {v} ]}
詹姆斯·克拉克·麦克斯韦 在四元数的基础建立了著名的麦克斯韦方程组 。四元数因此(同时也因为其他方面的)应用,在很长一段时间内都是物理学教育的必备内容。
在1878年威廉·金顿·克利福德 在发表的《Elements of Dynamic
四元数方法通常需要提取结果中的标量和矢量部分的信息,因此奥利弗·亥维赛 和乔赛亚·威拉德·吉布斯 都认为其过于冗长。于是在四元数乘法被引入约四十年后,他们在激烈的反对声中引入了点积和叉积以作为替代方案。新方法在效率上的便捷最终得到了一致认可,使得亥维赛 可以将麦克斯韦方程组由最初的20个减为今天常见的4个。
在很大程度上独立于这种发展,而且当时基本上不受欢迎,赫尔曼·格拉斯曼 发明了一种与二维和三维空间无关几何代数,外积在其中起着中心作用。在1853年,与格拉斯曼同时代的人奥古斯丁·路易·柯西 发表了一篇关于代数键的文章。代数键可用于求解方程,且和叉积有着相同的乘法特性。克利福德将哈密顿和格拉斯曼的代数结合起来,创建了克利福德代数 。在三维矢量的情况下,由两个矢量产生的双向量二重化为一个矢量,从而产生叉积。
交叉符号和“叉积”这个名字是从乔赛亚·威拉德·吉布斯 开始的,它们最初出现在1881年给他的学生的私人出版笔记中,叫做《向量分析的元素》。吉布斯的符号以及“叉乘”这个名字后来通过他以前的学生埃德温·B·威尔逊 Vector Analysis
第一,关于向量的加法和标量与向量的乘积。第二,关于微分和积分与标量函数和向量函数的关系。第三,包含了线性向量函数的理论。
定义了两个主要的向量乘法,称为:
两个向量的直接乘 ,标量乘 或者点乘 。
两个向量的斜乘 ,向量乘 或叉乘 。 还研究了几种三重积和三重以上向量的乘积。还包括上述的三重积扩展。















































































![{\displaystyle [-\mathbf {u} \cdot \mathbf {v} ,\mathbf {u} \times \mathbf {v} ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c9591e0498cf2afe14892668652ca0a1b38b4ece)