|
|
| (未显示2个用户的2个中间版本) |
| 第1行: |
第1行: |
|
{{NoteTA |
|
{{NoteTA |
|
|T=zh-cn:叉积;zh-hant:外積; |
|
| T = zh-cn:叉积;zh-hant:外積; |
|
|G1 = Math |
|
| G1 = Math|zh-hans:点积;zh-hant:內積; |
|
}} |
|
}} |
|
{{dablink|本文介绍向量的向量积。關於常稱作'''外積'''的相關二元運算,参见[[外积]]。}} |
|
{{dablink|本文介绍向量的向量积。關於常稱作'''外積'''的相關二元運算,参见[[外积]]。}} |
|
{{Linear algebra}} |
|
{{Linear algebra}} |
|
在[[数学]]和[[向量代数]]领域,'''外積'''({{lang-en|external product}})又称'''叉积'''({{lang|en|cross product}})、'''叉乘'''、'''向量积'''({{lang|en|vector product}}),是对[[三维空间]]中的两个[[向量]]的[[二元运算]],使用符号 <math>\times</math>。与[[点积]]不同,它的运算结果是[[向量]]。对于[[线性无关]]的两个向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math>,它们的外积写作 <math>\mathbf{a} \times \mathbf{b}</math>,是 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 所在平面的[[法线]]向量,与 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 都[[垂直]]。外积被广泛运用于数学、[[物理]]、[[工程学]]、[[计算机科学]]领域。 |
|
在[[数学]]和[[向量代数]]领域,'''外積'''({{lang-en|external product}})又称'''叉积'''({{lang|en|cross product}})、'''叉乘'''、'''向量积'''({{lang|en|vector product}}),是对[[三维空间]]中的两个[[向量]]的[[二元运算]],使用符号<math>\times</math>。与[[点积]]不同,它的运算结果是[[向量]]。对于[[线性无关]]的两个向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>,它们的外积写作<math>\mathbf{a} \times \mathbf{b}</math>,是<math>\mathbf{a}</math>和<math>\mathbf{b}</math>所在平面的[[法线]]向量,与<math>\mathbf{a}</math>和<math>\mathbf{b}</math>都[[垂直]]。外积被广泛运用于数学、[[物理]]、[[工程学]]、[[计算机科学]]领域。 |
|
|
|
|
|
如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零。推广开来,外积的[[模长]]和以这两个向量为边的[[平行四边形]]的面积相等;如果两个向量成直角,它们外积的模长即为两者长度的乘积。 |
|
如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零。推广开来,外积的[[模长]]和以这两个向量为边的[[平行四边形]]的面积相等;如果两个向量成直角,它们外积的模长即为两者长度的乘积。 |
| 第17行: |
第17行: |
|
== 定义 == |
|
== 定义 == |
|
[[File:Right hand rule cross product.svg|thumb|使用[[右手定則]]确定外积的方向]] |
|
[[File:Right hand rule cross product.svg|thumb|使用[[右手定則]]确定外积的方向]] |
|
两个向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 的外积仅在[[三维空间]]中有定义,写作 <math>\mathbf{a} \times \mathbf{b}</math>。在[[物理学]]中,外积有时也被写成<math>\mathbf{a} \wedge \mathbf{b}</math>,但在数学中 <math>\mathbf{a} \wedge \mathbf{b}</math> 是[[外代数]]中的外积。 |
|
两个向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>的外积仅在[[三维空间]]中有定义,写作<math>\mathbf{a} \times \mathbf{b}</math>。在[[物理学]]中,外积有时也被写成<math>\mathbf{a} \wedge \mathbf{b}</math>,但在数学中<math>\mathbf{a} \wedge \mathbf{b}</math>是[[外代数]]中的外积。 |
|
|
|
|
|
外积 <math>\mathbf{a} \times \mathbf{b}</math> 是与 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 都垂直的向量 <math>\mathbf{c}</math>。其方向由[[右手定則]]决定,[[范数]]等于以两个向量为边的[[平行四边形]]的[[面积]]。 |
|
外积<math>\mathbf{a} \times \mathbf{b}</math>是与<math>\mathbf{a}</math>和<math>\mathbf{b}</math>都垂直的向量<math>\mathbf{c}</math>。其方向由[[右手定則]]决定,[[范数]]等于以两个向量为边的[[平行四边形]]的[[面积]]。 |
|
|
|
|
|
外积可以定义为: |
|
外积可以定义为: |
| 第25行: |
第25行: |
|
:<math>\mathbf{a} \times \mathbf{b} = \| \mathbf{a} \| \| \mathbf{b} \| \sin(\theta) \ \mathbf{n}</math> |
|
:<math>\mathbf{a} \times \mathbf{b} = \| \mathbf{a} \| \| \mathbf{b} \| \sin(\theta) \ \mathbf{n}</math> |
|
|
|
|
|
其中 <math>\theta</math> 表示 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 在它们所定义的平面上的[[角度|夹角]](<math>0^\circ \le \theta \le 180^\circ</math>)。<math>\| \mathbf{a} \|</math> 和 <math>\| \mathbf{b} \|</math> 是向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 的[[模长]],而 <math>\mathbf{n}</math> 则是一个与 <math>\mathbf{a}</math>、<math>\mathbf{b}</math> 所构成的平面[[垂直]]的[[单位向量]],方向由[[右手定則]]决定。根据上述公式,当 <math>\mathbf{a}</math> 与 <math>\mathbf{b}</math> 平行(即 <math>\theta</math> 为 0° 或 180°)时,它们的外积为[[零向量]] <math>\mathbf{0}</math>。 |
|
其中<math>\theta</math>表示<math>\mathbf{a}</math>和<math>\mathbf{b}</math>在它们所定义的平面上的[[角度|夹角]](<math>0^\circ \le \theta \le 180^\circ</math>)。<math>\| \mathbf{a} \|</math>和<math>\| \mathbf{b} \|</math>是向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>的[[模长]],而<math>\mathbf{n}</math>则是一个与<math>\mathbf{a}</math>、<math>\mathbf{b}</math>所构成的平面[[垂直]]的[[单位向量]],方向由[[右手定則]]决定。根据上述公式,当<math>\mathbf{a}</math>与<math>\mathbf{b}</math>平行(即<math>\theta</math>为0°或180°)时,它们的外积为[[零向量]]<math>\mathbf{0}</math>。 |
|
|
|
|
|
[[File:Cross product.gif|thumb|外积{{nowrap|'''a''' × '''b'''}}(垂直方向、紫色)随着向量 '''a'''(蓝色)和 '''b'''(红色)的夹角变化。 外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖'''a'''‖‖'''b'''‖。]] |
|
[[File:Cross product.gif|thumb|外积{{nowrap|'''a''' × '''b'''}}(垂直方向、紫色)随着向量'''a'''(蓝色)和'''b'''(红色)的夹角变化。外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖'''a'''‖‖'''b'''‖。]] |
|
|
|
|
|
按照惯例,向量 <math>\mathbf{n}</math> 的方向由[[右手定則]]决定:将右手[[食指]]指向 <math>\mathbf{a}</math> 的方向、[[中指]]指向 <math>\mathbf{b}</math> 的方向,则此时[[拇指]]的方向即为 <math>\mathbf{n}</math> 的方向。使用这一定则意味着外积满足[[反交换律]],<math>\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})</math>:将右手食指指向 <math>\mathbf{b}</math>、中指指向 <math>\mathbf{a}</math>,那么拇指就必定指向相反方向,即翻转了外积的符号。 |
|
按照惯例,向量<math>\mathbf{n}</math>的方向由[[右手定則]]决定:将右手[[食指]]指向<math>\mathbf{a}</math>的方向、[[中指]]指向<math>\mathbf{b}</math>的方向,则此时[[拇指]]的方向即为<math>\mathbf{n}</math>的方向。使用这一定则意味着外积满足[[反交换律]],<math>\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})</math>:将右手食指指向<math>\mathbf{b}</math>、中指指向<math>\mathbf{a}</math>,那么拇指就必定指向相反方向,即翻转了外积的符号。 |
|
|
|
|
|
由此可以看出,使用外积需要考虑坐标系的利手性({{lang-en|Handedness}}),如果使用的是[[笛卡尔坐标系#三維空間|左手坐标系]],向量 <math>\mathbf{n}</math> 的方向需要使用[[左手定则]]决定,与右手坐标系中的方向相反。 |
|
由此可以看出,使用外积需要考虑坐标系的利手性({{lang-en|Handedness}}),如果使用的是[[笛卡尔坐标系#三維空間|左手坐标系]],向量<math>\mathbf{n}</math>的方向需要使用[[左手定则]]决定,与右手坐标系中的方向相反。 |
|
|
|
|
|
这样就会带来一个问题:[[参照系]]的变换不应该影响 <math>\mathbf{n}</math> 的方向(例如从右手坐标系到左手坐标系的镜像变换)。因此,两个向量的外积并不是(真)向量,而是[[贗向量]]。 |
|
这样就会带来一个问题:[[参照系]]的变换不应该影响<math>\mathbf{n}</math>的方向(例如从右手坐标系到左手坐标系的镜像变换)。因此,两个向量的外积并不是(真)向量,而是[[贗向量]]。 |
|
|
|
|
|
== 计算 == |
|
== 计算 == |
| 第39行: |
第39行: |
|
=== 坐标表示 === |
|
=== 坐标表示 === |
|
|
|
|
|
[[File:3D Vector.svg|300px|thumb|right|[[基向量]]('''i'''、'''j'''、'''k''',也记作 '''e'''<sub>1</sub>、'''e'''<sub>2</sub>、'''e'''<sub>3</sub>)和[[向量]] '''a''' 的分解('''a'''<sub>x</sub>、'''a'''<sub>y</sub>、'''a'''<sub>z</sub>,也记作 '''a'''<sub>1</sub>、'''a'''<sub>2</sub>、'''a'''<sub>3</sub>)]] |
|
[[File:3D Vector.svg|300px|thumb|right|[[基向量]]('''i'''、'''j'''、'''k''',也记作'''e'''<sub>1</sub>、'''e'''<sub>2</sub>、'''e'''<sub>3</sub>)和[[向量]]'''a'''的分解('''a'''<sub>x</sub>、'''a'''<sub>y</sub>、'''a'''<sub>z</sub>,也记作'''a'''<sub>1</sub>、'''a'''<sub>2</sub>、'''a'''<sub>3</sub>)]] |
|
|
|
|
|
右手坐标系中,[[基向量]] <math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math> 满足以下等式: |
|
右手坐标系中,[[基向量]]<math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math>满足以下等式: |
|
:<math>\begin{align} |
|
:<math>\begin{align} |
|
\mathbf{i}\times\mathbf{j} &= \mathbf{k}\\ |
|
\mathbf{i}\times\mathbf{j} &= \mathbf{k}\\ |
| 第60行: |
第60行: |
|
根据以上等式,结合外积的[[分配律]]和[[线性关系]],就可以确定任意向量的外积。 |
|
根据以上等式,结合外积的[[分配律]]和[[线性关系]],就可以确定任意向量的外积。 |
|
|
|
|
|
向量 <math>\mathbf{u}</math> 和 <math>\mathbf{v}</math> 可以定义为平行于[[基向量]]的三个正交元素之和: |
|
向量<math>\mathbf{u}</math>和<math>\mathbf{v}</math>可以定义为平行于[[基向量]]的三个正交元素之和: |
|
:<math>\begin{align} |
|
:<math>\begin{align} |
|
\mathbf{u} &= u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k} \\ |
|
\mathbf{u} &= u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k} \\ |
| 第66行: |
第66行: |
|
\end{align}</math> |
|
\end{align}</math> |
|
|
|
|
|
两者的外积 <math>\mathbf{u} \times \mathbf{v}</math> 可以根据[[分配律]]展开: |
|
两者的外积<math>\mathbf{u} \times \mathbf{v}</math>可以根据[[分配律]]展开: |
|
:<math> \begin{align} |
|
:<math> \begin{align} |
|
\mathbf{u}\times\mathbf{v} = {} &(u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k}) \times (v_1\mathbf{i} + v_2\mathbf{j} + v_3\mathbf{k})\\ |
|
\mathbf{u}\times\mathbf{v} = {} &(u_1\mathbf{i} + u_2\mathbf{j} + u_3\mathbf{k}) \times (v_1\mathbf{i} + v_2\mathbf{j} + v_3\mathbf{k})\\ |
| 第74行: |
第74行: |
|
\end{align}</math> |
|
\end{align}</math> |
|
|
|
|
|
即把 <math>\mathbf{u} \times \mathbf{v}</math> 分解为九个仅涉及 <math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math> 的简单外积之和。九个外积各自所涉及的向量,要么相互平行、要么相互正交。将最前面所述的几个等式带入其中,然后合并同类项,可以得到: |
|
即把<math>\mathbf{u} \times \mathbf{v}</math>分解为九个仅涉及<math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math>的简单外积之和。九个外积各自所涉及的向量,要么相互平行、要么相互正交。将最前面所述的几个等式带入其中,然后合并同类项,可以得到: |
|
:<math>\begin{align} |
|
:<math>\begin{align} |
|
\mathbf{u}\times\mathbf{v} = {} &- u_1v_1\mathbf{0} + u_1v_2\mathbf{k} - u_1v_3\mathbf{j} \\ |
|
\mathbf{u}\times\mathbf{v} = {} &- u_1v_1\mathbf{0} + u_1v_2\mathbf{k} - u_1v_3\mathbf{j} \\ |
| 第82行: |
第82行: |
|
\end{align}</math> |
|
\end{align}</math> |
|
|
|
|
|
即结果向量 <math>\mathbf{s} = s_1\mathbf{i} + s_2\mathbf{j} + s_3\mathbf{k} = \mathbf{u} \times \mathbf{v} </math> 的三个[[标量 (数学)|标量]]元素为: |
|
即结果向量<math>\mathbf{s} = s_1\mathbf{i} + s_2\mathbf{j} + s_3\mathbf{k} = \mathbf{u} \times \mathbf{v} </math>的三个[[标量 (数学)|标量]]元素为: |
|
:<math>\begin{align} |
|
:<math>\begin{align} |
|
s_1 &= u_2v_3-u_3v_2\\ |
|
s_1 &= u_2v_3-u_3v_2\\ |
| 第90行: |
第90行: |
|
|
|
|
|
也可以记作[[列向量]]的形式: |
|
也可以记作[[列向量]]的形式: |
|
:<math>\begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix}=\begin{pmatrix}u_2v_3-u_3v_2\\u_3v_1-u_1v_3\\u_1v_2-u_2v_1\end{pmatrix}</math> |
|
:<math>\begin{pmatrix}s_1,s_2,s_3\end{pmatrix}=\begin{pmatrix}u_2v_3-u_3v_2,u_3v_1-u_1v_3,u_1v_2-u_2v_1\end{pmatrix}</math> |
|
|
|
|
|
=== 矩阵表示 === |
|
=== 矩阵表示 === |
|
|
|
|
|
[[File:Sarrus rule cross product.svg|thumb|根据[[萨吕法则]]确定 '''u''' 和 '''v''' 的外积]] |
|
[[File:Sarrus rule cross product.svg|thumb|根据[[萨吕法则]]确定'''u'''和'''v'''的外积]] |
|
|
|
|
|
外积可以表达为这样的[[行列式]]: |
|
外积可以表达为这样的[[行列式]]: |
| 第132行: |
第132行: |
|
===代数性质 === |
|
===代数性质 === |
|
|
|
|
|
對於任意三個向量 <math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math>, |
|
對於任意三個向量<math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math>, |
|
*<math>\mathbf{a} \times \mathbf{a} = \mathbf{0}</math> |
|
*<math>\mathbf{a} \times \mathbf{a} = \mathbf{0}</math> |
|
*<math>\mathbf{a} \times \mathbf{0} = \mathbf{0}</math> |
|
*<math>\mathbf{a} \times \mathbf{0} = \mathbf{0}</math> |
| 第146行: |
第146行: |
|
\end{vmatrix}</math>([[拉格朗日恆等式]]) |
|
\end{vmatrix}</math>([[拉格朗日恆等式]]) |
|
|
|
|
|
一般來說,向量外積不遵守[[約簡律]],即 <math>\mathbf{a} \times \mathbf{b} = \mathbf{a} \times \mathbf{c}</math> 不表示 <math>\mathbf{b} = \mathbf{c}</math>。此外,<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math> 不表示 <math>\mathbf{a} = \mathbf{0}</math> 或 <math>\mathbf{b} = \mathbf{0}</math>。 |
|
一般來說,向量外積不遵守[[約簡律]],即<math>\mathbf{a} \times \mathbf{b} = \mathbf{a} \times \mathbf{c}</math>不表示<math>\mathbf{b} = \mathbf{c}</math>。此外,<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math>不表示<math>\mathbf{a} = \mathbf{0}</math>或<math>\mathbf{b} = \mathbf{0}</math>。 |
|
|
|
|
|
但對於两个非零向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math>, |
|
但對於两个非零向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>, |
|
*<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math> [[當且僅當]] <math>\mathbf{a}</math> 平行於 <math>\mathbf{b}</math> |
|
*<math>\mathbf{a} \times \mathbf{b} = \mathbf{0}</math>[[當且僅當]] <math>\mathbf{a}</math>平行於<math>\mathbf{b}</math> |
|
|
|
|
|
=== 几何意义 === |
|
=== 几何意义 === |
| 第156行: |
第156行: |
|
[[File:Parallelepiped volume.svg|right|thumb|240px|图2:三个向量定义平行六面体]] |
|
[[File:Parallelepiped volume.svg|right|thumb|240px|图2:三个向量定义平行六面体]] |
|
|
|
|
|
如果以向量 <math>\mathbf{a}</math> 和 <math>\mathbf{b}</math> 为边构成一个[[平行四边形]],那么这两个向量外积的[[模长]]与这个平行四边形的正[[面积]]相等(如图1): |
|
如果以向量<math>\mathbf{a}</math>和<math>\mathbf{b}</math>为边构成一个[[平行四边形]],那么这两个向量外积的[[范数]]与这个平行四边形的正[[面积]]相等(如图1): |
|
:<math> \left\| \mathbf{a} \times \mathbf{b} \right\| = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin \theta .</math> |
|
:<math> \left\| \mathbf{a} \times \mathbf{b} \right\| = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin \theta .</math> |
|
|
|
|
|
同时,如果以向量 <math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math> 为棱构成一个[[平行六面体]],那么这个平行六面体的[[体积]] <math>\mathbf{V}</math> 也可以通过外积和点积的组合得到,这种积称作[[三重积#标量三重积|标量三重积]](如图2): |
|
同时,如果以向量<math>\mathbf{a}</math>、<math>\mathbf{b}</math>、<math>\mathbf{c}</math>为棱构成一个[[平行六面体]],那么这个平行六面体的[[体积]]<math>\mathbf{V}</math>也可以通过外积和点积的组合得到,这种积称作[[三重积#标量三重积|标量三重积]](如图2): |
|
:<math> |
|
:<math> |
|
\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})= |
|
\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})= |
| 第174行: |
第174行: |
|
|
|
|
|
===向量微分=== |
|
===向量微分=== |
|
對於實數 <math>t</math> 和兩個向量值函數 <math>\mathbf{a}(t)</math>、<math>\mathbf{b}(t)</math>,[[乘積法則]]成立: |
|
對於實數<math>t</math>和兩個向量值函數<math>\mathbf{a}(t)</math>、<math>\mathbf{b}(t)</math>,[[乘積法則]]成立: |
|
*<math>\frac{d}{dt}(\mathbf{a} \times \mathbf{b}) = \frac{d\mathbf{a}}{dt} \times \mathbf{b} + \mathbf{a} \times \frac{d\mathbf{b}}{dt}</math> |
|
*<math>\frac{d}{dt}(\mathbf{a} \times \mathbf{b}) = \frac{d\mathbf{a}}{dt} \times \mathbf{b} + \mathbf{a} \times \frac{d\mathbf{b}}{dt}</math> |
|
|
|
|
| 第199行: |
第199行: |
|
\end{align}</math> |
|
\end{align}</math> |
|
|
|
|
|
外积也可以用[[四元数]]来表示。注意到上述 <math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math> 之间的外积满足四元数的乘法。一般而言,若将向量[''a''<sub>1</sub>, ''a''<sub>2</sub>, ''a''<sub>3</sub>]表示成四元数''a''<sub>1</sub>''i'' + ''a''<sub>2</sub>''j'' + ''a''<sub>3</sub>''k'',两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见[[四元数与空间旋转]]。 |
|
外积也可以用[[四元数]]来表示。注意到上述<math>\mathbf{i}</math>、<math>\mathbf{j}</math>、<math>\mathbf{k}</math>之间的外积满足四元数的乘法。一般而言,若将向量[''a''<sub>1</sub>, ''a''<sub>2</sub>, ''a''<sub>3</sub>]表示成四元数''a''<sub>1</sub>''i'' + ''a''<sub>2</sub>''j'' + ''a''<sub>3</sub>''k'',两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见[[四元数与空间旋转]]。 |
|
|
|
|
|
== 高维情形 == |
|
== 高维情形 == |
| 第212行: |
第212行: |
|
:<math>\mathbf{x} \times \mathbf{y} + \mathbf{y} \times \mathbf{x} = \mathbf{0}</math> |
|
:<math>\mathbf{x} \times \mathbf{y} + \mathbf{y} \times \mathbf{x} = \mathbf{0}</math> |
|
|
|
|
|
*<math>\mathbf{x} \times \mathbf{y}</math> 同时与 <math>\mathbf{x}</math> 和 <math>\mathbf{y}</math> 垂直: |
|
*<math>\mathbf{x} \times \mathbf{y}</math>同时与<math>\mathbf{x}</math>和<math>\mathbf{y}</math>垂直: |
|
:<math>\mathbf{x} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{y} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{0}</math> |
|
:<math>\mathbf{x} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{y} \cdot (\mathbf{x} \times \mathbf{y}) = \mathbf{0}</math> |
|
|
|
|

本文介绍向量的向量积。關於常稱作
外積的相關二元運算,参见
外积。
| 线性代数
|
 |
| 向量 · 向量空间 · 基底 · 行列式 · 矩阵
|
|
|
|
|
在数学和向量代数领域,外積(英語:external product)又称叉积(cross product)、叉乘、向量积(vector product),是对三维空间中的两个向量的二元运算,使用符号 。与点积不同,它的运算结果是向量。对于线性无关的两个向量
。与点积不同,它的运算结果是向量。对于线性无关的两个向量 和
和 ,它们的外积写作
,它们的外积写作 ,是
,是 和
和 所在平面的法线向量,与
所在平面的法线向量,与 和
和 都垂直。外积被广泛运用于数学、物理、工程学、计算机科学领域。
都垂直。外积被广泛运用于数学、物理、工程学、计算机科学领域。
如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零。推广开来,外积的模长和以这两个向量为边的平行四边形的面积相等;如果两个向量成直角,它们外积的模长即为两者长度的乘积。
外积和点积一样依赖于欧几里德空间的度量,但与点积之不同的是,外积还依赖于定向或右手定則。
叉积的名称源自表示叉积运算的叉乘号( ),讀作
),讀作a cross b,向量积的叫法则是在强调其运算结果为向量而非标量。向量的另一种乘法是点积( ),讀作
),讀作a dot b,其结果为标量,称为点积或数量积或标量积。
 在右手坐标系中的向量积
在右手坐标系中的向量积
 使用右手定則确定外积的方向
使用右手定則确定外积的方向
两个向量 和
和 的外积仅在三维空间中有定义,写作
的外积仅在三维空间中有定义,写作 。在物理学中,外积有时也被写成
。在物理学中,外积有时也被写成 ,但在数学中
,但在数学中 是外代数中的外积。
是外代数中的外积。
外积 是与
是与 和
和 都垂直的向量
都垂直的向量 。其方向由右手定則决定,范数等于以两个向量为边的平行四边形的面积。
。其方向由右手定則决定,范数等于以两个向量为边的平行四边形的面积。
外积可以定义为:

其中 表示
表示 和
和 在它们所定义的平面上的夹角(
在它们所定义的平面上的夹角( )。
)。 和
和 是向量
是向量 和
和 的模长,而
的模长,而 则是一个与
则是一个与 、
、 所构成的平面垂直的单位向量,方向由右手定則决定。根据上述公式,当
所构成的平面垂直的单位向量,方向由右手定則决定。根据上述公式,当 与
与 平行(即
平行(即 为0°或180°)时,它们的外积为零向量
为0°或180°)时,它们的外积为零向量 。
。
 外积a × b(垂直方向、紫色)随着向量a(蓝色)和b(红色)的夹角变化。外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖a‖‖b‖。
外积a × b(垂直方向、紫色)随着向量a(蓝色)和b(红色)的夹角变化。外积垂直于两个向量,模长在两者平行时为零、在两者垂直时达到最大值‖a‖‖b‖。
按照惯例,向量 的方向由右手定則决定:将右手食指指向
的方向由右手定則决定:将右手食指指向 的方向、中指指向
的方向、中指指向 的方向,则此时拇指的方向即为
的方向,则此时拇指的方向即为 的方向。使用这一定则意味着外积满足反交换律,
的方向。使用这一定则意味着外积满足反交换律, :将右手食指指向
:将右手食指指向 、中指指向
、中指指向 ,那么拇指就必定指向相反方向,即翻转了外积的符号。
,那么拇指就必定指向相反方向,即翻转了外积的符号。
由此可以看出,使用外积需要考虑坐标系的利手性(英語:Handedness),如果使用的是左手坐标系,向量 的方向需要使用左手定则决定,与右手坐标系中的方向相反。
的方向需要使用左手定则决定,与右手坐标系中的方向相反。
这样就会带来一个问题:参照系的变换不应该影响 的方向(例如从右手坐标系到左手坐标系的镜像变换)。因此,两个向量的外积并不是(真)向量,而是贗向量。
的方向(例如从右手坐标系到左手坐标系的镜像变换)。因此,两个向量的外积并不是(真)向量,而是贗向量。
 基向量(i、j、k,也记作e1、e2、e3)和向量a的分解(ax、ay、az,也记作a1、a2、a3)
基向量(i、j、k,也记作e1、e2、e3)和向量a的分解(ax、ay、az,也记作a1、a2、a3)
右手坐标系中,基向量 、
、 、
、 满足以下等式:
满足以下等式:

根据反交换律可以得出:

根据外积的定义可以得出:
 (零向量)。
(零向量)。
根据以上等式,结合外积的分配律和线性关系,就可以确定任意向量的外积。
向量 和
和 可以定义为平行于基向量的三个正交元素之和:
可以定义为平行于基向量的三个正交元素之和:

两者的外积 可以根据分配律展开:
可以根据分配律展开:

即把 分解为九个仅涉及
分解为九个仅涉及 、
、 、
、 的简单外积之和。九个外积各自所涉及的向量,要么相互平行、要么相互正交。将最前面所述的几个等式带入其中,然后合并同类项,可以得到:
的简单外积之和。九个外积各自所涉及的向量,要么相互平行、要么相互正交。将最前面所述的几个等式带入其中,然后合并同类项,可以得到:

即结果向量 的三个标量元素为:
的三个标量元素为:

也可以记作列向量的形式:

 根据萨吕法则确定u和v的外积
根据萨吕法则确定u和v的外积
外积可以表达为这样的行列式:
 [1]
[1]
这个行列式可以使用萨吕法则或拉普拉斯展开计算。使用萨吕法则可以展开为:

使用拉普拉斯展开可以沿第一行展开为:[2]

都可以直接得到结果向量。
對於任意三個向量 、
、 、
、 ,
,


 (反交换律)
(反交换律) (加法的左分配律)
(加法的左分配律) (加法的右分配律)
(加法的右分配律)


 (拉格朗日恆等式)
(拉格朗日恆等式)
一般來說,向量外積不遵守約簡律,即 不表示
不表示 。此外,
。此外, 不表示
不表示 或
或 。
。
但對於两个非零向量 和
和 ,
,
 當且僅當
當且僅當  平行於
平行於
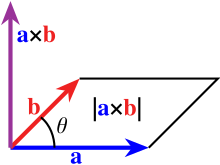 图1:平行四边形面积即外积的模长
图1:平行四边形面积即外积的模长
 图2:三个向量定义平行六面体
图2:三个向量定义平行六面体
如果以向量 和
和 为边构成一个平行四边形,那么这两个向量外积的范数与这个平行四边形的正面积相等(如图1):
为边构成一个平行四边形,那么这两个向量外积的范数与这个平行四边形的正面积相等(如图1):

同时,如果以向量 、
、 、
、 为棱构成一个平行六面体,那么这个平行六面体的体积
为棱构成一个平行六面体,那么这个平行六面体的体积 也可以通过外积和点积的组合得到,这种积称作标量三重积(如图2):
也可以通过外积和点积的组合得到,这种积称作标量三重积(如图2):

因为标量三重积可能为负,平行六面体的体积需要取其绝对值:

因为外积的模长与其参数夹角的正弦有关,可以认为外积是「垂直度」的度量,正如点积是「平行度」的度量一样。对于任意两个单位向量,外积为1意味着它们互相垂直,外积为0意味着它们互相平行。点积则相反:点积为0意味着它们互相垂直。
单位向量还能带来两个特性:两个单位向量的点积是它们夹角的余弦(可正可负);它们外积的模长则为夹角的正弦(始终为正)。
對於實數 和兩個向量值函數
和兩個向量值函數 、
、 ,乘積法則成立:
,乘積法則成立:

给定直角坐标系的单位向量 ,
, ,
, 满足下列等式:
满足下列等式:
 、
、 、
、
通过这些规则,两个向量的外积的坐标可以方便地计算出来,不需要考虑任何角度:设


则

外积也可以用四元数来表示。注意到上述 、
、 、
、 之间的外积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
之间的外积满足四元数的乘法。一般而言,若将向量[a1, a2, a3]表示成四元数a1i + a2j + a3k,两个向量的外积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
七维向量的外积可以通过八元数得到,与上述的四元数方法相同。
七维外积具有与三维外积相似的性质:



 同时与
同时与 和
和 垂直:
垂直:



另外,在物理学力学、电磁学、光学和计算机图形学等理工学科中,外积应用十分广泛。例如力矩、角动量、洛伦兹力等矢量都可以由向量的外积求解。在进行这些物理量的计算时,往往可以借助右手定则辅助判断方向。
1773年,约瑟夫·拉格朗日引入了点积和叉积的概念来研究三维空间中的四面体。1843年,威廉·哈密顿引入了四元数乘法,同时区分了“向(矢)量”和“标量”的概念。给定两个四元数[0,u]和[0,v],其中u和v是 空间中的向量,使得其乘积可以写成为
空间中的向量,使得其乘积可以写成为![{\displaystyle [-\mathbf {u} \cdot \mathbf {v} ,\mathbf {u} \times \mathbf {v} ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c9591e0498cf2afe14892668652ca0a1b38b4ece) 的形式。詹姆斯·克拉克·麦克斯韦在四元数的基础建立了著名的麦克斯韦方程组。四元数因此(同时也因为其他方面的)应用,在很长一段时间内都是物理学教育的必备内容。
的形式。詹姆斯·克拉克·麦克斯韦在四元数的基础建立了著名的麦克斯韦方程组。四元数因此(同时也因为其他方面的)应用,在很长一段时间内都是物理学教育的必备内容。
在1878年威廉·金顿·克利福德在发表的《Elements of Dynamic》中将两个向量的叉积的范数定义为以这两个向量为边的平行四边形的面积,且在在方向上垂直于它们所确定的平面。
四元数方法通常需要提取结果中的标量和矢量部分的信息,因此奥利弗·亥维赛和乔赛亚·威拉德·吉布斯都认为其过于冗长。于是在四元数乘法被引入约四十年后,他们在激烈的反对声中引入了点积和叉积以作为替代方案。新方法在效率上的便捷最终得到了一致认可,使得亥维赛可以将麦克斯韦方程组由最初的20个减为今天常见的4个。
在很大程度上独立于这种发展,而且当时基本上不受欢迎,赫尔曼·格拉斯曼发明了一种与二维和三维空间无关几何代数,外积在其中起着中心作用。在1853年,与格拉斯曼同时代的人奥古斯丁·路易·柯西发表了一篇关于代数键的文章。代数键可用于求解方程,且和叉积有着相同的乘法特性。克利福德将哈密顿和格拉斯曼的代数结合起来,创建了克利福德代数。在三维矢量的情况下,由两个矢量产生的双向量二重化为一个矢量,从而产生叉积。
交叉符号和“叉积”这个名字是从乔赛亚·威拉德·吉布斯开始的,它们最初出现在1881年给他的学生的私人出版笔记中,叫做《向量分析的元素》。吉布斯的符号以及“叉乘”这个名字后来通过他以前的学生埃德温·B·威尔逊编写的教科书《向量分析》(Vector Analysis)获得了广泛的读者。威尔逊从吉布斯的课件中重新组织了材料,以及Heaviside,Föpps和Hamilton出版的材料。他把向量分析分为下列三个部分:
第一,关于向量的加法和标量与向量的乘积。第二,关于微分和积分与标量函数和向量函数的关系。第三,包含了线性向量函数的理论。
定义了两个主要的向量乘法,称为:
- 两个向量的直接乘,标量乘或者点乘。
- 两个向量的斜乘,向量乘或叉乘。
还研究了几种三重积和三重以上向量的乘积。还包括上述的三重积扩展。
















































































![{\displaystyle [-\mathbf {u} \cdot \mathbf {v} ,\mathbf {u} \times \mathbf {v} ]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c9591e0498cf2afe14892668652ca0a1b38b4ece)