拋物線座標系:修订间差异
Stuntaling(留言 | 贡献) 无编辑摘要 |
小 →top |
||
| (未显示12个用户的16个中间版本) | |||
| 第1行: | 第1行: | ||
[[File:Parabolic_coords.svg|thumb| |
[[File:Parabolic_coords.svg|thumb|right|400px|拋物線坐標系的綠色的 <math>\sigma</math> 等值曲線和紅色的 <math>\tau</math> 等值曲線。横軸與縱軸分別為 x-軸與 y-軸。]] |
||
'''拋物線坐標系'''({{lang-en|Parabolic coordinates}})是一種二維[[正交坐標系]],兩個坐標的等值曲線都是共焦的[[拋物線]]。將二維的拋物線坐標系繞著[[拋物線]]的對稱軸旋轉,則可以得到三維的拋物線坐標系。 |
'''拋物線坐標系'''({{lang-en|Parabolic coordinates}})是一種二維[[正交坐標系]],兩個坐標的等值曲線都是共焦的[[拋物線]]。將二維的拋物線坐標系繞著[[拋物線]]的對稱軸旋轉,則可以得到三維的拋物線坐標系。 |
||
| 第6行: | 第6行: | ||
==二維拋物線坐標系== |
==二維拋物線坐標系== |
||
直角坐標<math>(x,\ y)</math>可以用二維拋物線坐標<math>(\sigma,\ \tau)</math>表示為 |
直角坐標 <math>(x,\ y)</math> 可以用二維拋物線坐標 <math>(\sigma,\ \tau)</math> 表示為 |
||
:<math>x = \pm\,\sigma \tau</math>、 |
:<math>x = \pm\,\sigma \tau</math> 、 |
||
:<math>y = \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right)</math>; |
:<math>y = \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right)</math> ; |
||
其中,<math>\sigma\ge 0</math>,<math>\tau\ge 0</math>。 |
其中,<math>\sigma\ge 0</math> ,<math>\tau\ge 0</math> 。 |
||
反算回來,二維拋物線坐標<math>(\sigma,\ \tau)</math>可以用直角坐標<math>(x,\ y)</math>表示為 |
反算回來,二維拋物線坐標 <math>(\sigma,\ \tau)</math> 可以用直角坐標 <math>(x,\ y)</math> 表示為 |
||
:<math>\sigma=\sqrt{ - y +\sqrt{x^2+y^2}}</math>、 |
:<math>\sigma=\sqrt{ - y +\sqrt{x^2+y^2}}</math> 、 |
||
:<math>\tau=\sqrt{y +\sqrt{x^2+y^2}}</math>。 |
:<math>\tau=\sqrt{y +\sqrt{x^2+y^2}}</math> 。 |
||
坐標<math>\sigma</math>為常數的曲線形成共焦的,[[凸集|凹性]]向上的(往 +y-軸)[[拋物線]]: |
坐標 <math>\sigma</math> 為常數的曲線形成共焦的,[[凸集|凹性]]向上的(往 +y-軸)[[拋物線]]: |
||
:<math>2y = \frac{x^{2}}{\sigma^{2}} - \sigma^{2}</math>, |
:<math>2y = \frac{x^{2}}{\sigma^{2}} - \sigma^{2}</math> , |
||
而坐標<math>\tau</math> 為常數的曲線形成共焦的,[[凸集|凹性]]向下的(往 -y-軸)[[拋物線]]: |
而坐標 <math>\tau</math> 為常數的曲線形成共焦的,[[凸集|凹性]]向下的(往 -y-軸)[[拋物線]]: |
||
:<math>2y = - \frac{x^{2}}{\tau^{2}} + \tau^{2}</math>。 |
:<math>2y = - \frac{x^{2}}{\tau^{2}} + \tau^{2}</math> 。 |
||
這些拋物線的焦點的位置都在原點。 |
這些拋物線的焦點的位置都在原點。 |
||
| 第26行: | 第26行: | ||
==二維標度因子== |
==二維標度因子== |
||
拋物線坐標<math>(\sigma,\ \tau)</math>的標度因子相等: |
拋物線坐標 <math>(\sigma,\ \tau)</math> 的標度因子相等: |
||
:<math>h_{\sigma} = h_{\tau} = \sqrt{\sigma^{2} + \tau^{2}}</math>。 |
:<math>h_{\sigma} = h_{\tau} = \sqrt{\sigma^{2} + \tau^{2}}</math> 。 |
||
因此,面積的無窮小元素是 |
因此,面積的無窮小元素是 |
||
:<math>dA = \left( \sigma^{2} + \tau^{2} \right) d\sigma d\tau</math>。 |
:<math>dA = \left( \sigma^{2} + \tau^{2} \right) d\sigma d\tau</math> 。 |
||
[[拉普拉斯算子]]是 |
[[拉普拉斯算子]]是 |
||
:<math>\nabla^{2} \Phi = \frac{1}{\sigma^{2} + \tau^{2}} |
:<math>\nabla^{2} \Phi = \frac{1}{\sigma^{2} + \tau^{2}} |
||
\left( \frac{\partial^{2} \Phi}{\partial \sigma^{2}} + |
\left( \frac{\partial^{2} \Phi}{\partial \sigma^{2}} + |
||
\frac{\partial^{2} \Phi}{\partial \tau^{2}} \right)</math>。 |
\frac{\partial^{2} \Phi}{\partial \tau^{2}} \right)</math> 。 |
||
其它微分算子,像<math>\nabla \cdot \mathbf{F}</math>,<math>\nabla \times \mathbf{F}</math>,都可以用<math>(\sigma,\ \tau)</math>坐標表示,只要將標度因子代入在[[正交坐標系]]條目內的一般公式。 |
其它微分算子,像 <math>\nabla \cdot \mathbf{F}</math> , <math>\nabla \times \mathbf{F}</math> ,都可以用 <math>(\sigma,\ \tau)</math> 坐標表示,只要將標度因子代入在[[正交坐標系]]條目內的一般公式。 |
||
==三維拋物線坐標系== |
==三維拋物線坐標系== |
||
[[File:Parabolic_coordinates_3D.png|thumb|200px|三維拋物線坐標的[[坐標曲面]]。紅色的拋物曲面的坐標<math>\tau=2</math>。藍色的拋物曲面的坐標<math>\sigma=1</math>。黃色的半平面的坐標<math>\phi= - 60^\circ</math>。三個面相交於點<math>\mathbf{P}= (1.0, -1.732, 1.5)</math>(以黑色小球表示)。]] |
[[File:Parabolic_coordinates_3D.png|thumb|right|200px|三維拋物線坐標的[[坐標曲面]]。紅色的拋物曲面的坐標 <math>\tau=2</math> 。藍色的拋物曲面的坐標 <math>\sigma=1</math> 。黃色的半平面的坐標 <math>\phi= - 60^\circ</math> 。三個面相交於點 <math>\mathbf{P}= (1.0, -1.732, 1.5)</math> (以黑色小球表示)。]] |
||
將二維的拋物線坐標系繞著[[拋物線]]的對稱軸旋轉,則可以得到三維的拋物線坐標系,又稱為'''旋轉拋物線坐標系'''。將對稱軸與z-軸排列成同直線;而拋物線坐標系的共焦點與直角坐標系的原點同地點。直角坐標<math>(x,\ y,\ z)</math>可以用三維拋物線坐標<math>(\sigma,\ \tau,\ \phi)</math>表示為 |
將二維的拋物線坐標系繞著[[拋物線]]的對稱軸旋轉,則可以得到三維的拋物線坐標系,又稱為'''旋轉拋物線坐標系'''。將對稱軸與 z-軸排列成同直線;而拋物線坐標系的共焦點與直角坐標系的原點同地點。直角坐標 <math>(x,\ y,\ z)</math> 可以用三維拋物線坐標 <math>(\sigma,\ \tau,\ \phi)</math> 表示為 |
||
:<math>x=\sigma\tau\cos\phi</math>、 |
:<math>x=\sigma\tau\cos\phi</math> 、 |
||
:<math>y=\sigma\tau\sin\phi</math>、 |
:<math>y=\sigma\tau\sin\phi</math> 、 |
||
:<math>z=\frac{1}{2}\left(\tau^{2} - \sigma^{2}\right)</math>; |
:<math>z=\frac{1}{2}\left(\tau^{2} - \sigma^{2}\right)</math> ; |
||
其中,<math>\sigma\ge 0</math>,<math>\tau\ge 0</math>,方位角<math>\phi</math>定義為 |
其中,<math>\sigma\ge 0</math> ,<math>\tau\ge 0</math> ,方位角 <math>\phi</math> 定義為 |
||
:<math>\tan \phi = \frac{y}{x},\qquad 0\le \phi\le 2\pi</math>。 |
:<math>\tan \phi = \frac{y}{x},\qquad 0\le \phi\le 2\pi</math> 。 |
||
反算回來,三維拋物線坐標<math>(\sigma,\ \tau,\ \phi)</math>可以用直角坐標<math>(x,\ y,\ z)</math>表示為 |
反算回來,三維拋物線坐標 <math>(\sigma,\ \tau,\ \phi)</math> 可以用直角坐標 <math>(x,\ y,\ z)</math> 表示為 |
||
:<math>\sigma=\sqrt{ - z +\sqrt{x^2+y^2+z^2}}</math>、 |
:<math>\sigma=\sqrt{ - z +\sqrt{x^2+y^2+z^2}}</math> 、 |
||
:<math>\tau=\sqrt{z +\sqrt{x^2+y^2+z^2}}</math>、 |
:<math>\tau=\sqrt{z +\sqrt{x^2+y^2+z^2}}</math> 、 |
||
:<math>\phi =\tan^{ - 1}\frac{y}{x}</math>。 |
:<math>\phi =\tan^{ - 1}\frac{y}{x}</math> 。 |
||
每一個<math>\sigma</math>-坐標曲面都是共焦的,凹性向上的(往 +z-軸)'''拋物曲面''': |
每一個 <math>\sigma</math>-坐標曲面都是共焦的,凹性向上的(往 +z-軸)'''拋物曲面''': |
||
:<math>2z = \frac{x^{2} + y^{2}}{\sigma^{2}} - \sigma^{2}</math>, |
:<math>2z = \frac{x^{2} + y^{2}}{\sigma^{2}} - \sigma^{2}</math> , |
||
而每一個<math>\tau</math>>-坐標曲面都是共焦的,凹性向下的(往 -z-軸)'''拋物曲面''': |
而每一個 <math>\tau</math>>-坐標曲面都是共焦的,凹性向下的(往 -z-軸)'''拋物曲面''': |
||
:<math>2z = - \frac{x^{2} + y^{2}}{\tau^{2}} + \tau^{2}</math>。 |
:<math>2z = - \frac{x^{2} + y^{2}}{\tau^{2}} + \tau^{2}</math> 。 |
||
這些拋物曲面的焦點的位置都在原點。 |
這些拋物曲面的焦點的位置都在原點。 |
||
| 第66行: | 第66行: | ||
==三維標度因子== |
==三維標度因子== |
||
三維標度因子為: |
三維標度因子為: |
||
:<math>h_{\sigma} = \sqrt{\sigma^2+\tau^2}</math>、 |
:<math>h_{\sigma} = \sqrt{\sigma^2+\tau^2}</math> 、 |
||
:<math>h_{\tau} = \sqrt{\sigma^2+\tau^2}</math>、 |
:<math>h_{\tau} = \sqrt{\sigma^2+\tau^2}</math> 、 |
||
:<math>h_{\phi} = \sigma\tau\,</math>。 |
:<math>h_{\phi} = \sigma\tau\,</math> 。 |
||
我們可以觀察出,標度因子<math>h_{\sigma}</math>,<math>h_{\tau}</math>與二維標度因子相同。因此,體積的無窮小元素是 |
我們可以觀察出,標度因子 <math>h_{\sigma}</math> , <math>h_{\tau}</math> 與二維標度因子相同。因此,體積的無窮小元素是 |
||
:<math>dV = h_\sigma h_\tau h_\phi = \sigma\tau \left( \sigma^{2} + \tau^{2} \right)\,d\sigma\,d\tau\,d\phi</math>。 |
:<math>dV = h_\sigma h_\tau h_\phi = \sigma\tau \left( \sigma^{2} + \tau^{2} \right)\,d\sigma\,d\tau\,d\phi</math> 。 |
||
[[拉普拉斯算子]]是 |
[[拉普拉斯算子]]是 |
||
| 第80行: | 第80行: | ||
\left( \tau \frac{\partial \Phi}{\partial \tau} \right)\right] + |
\left( \tau \frac{\partial \Phi}{\partial \tau} \right)\right] + |
||
\frac{1}{\sigma^2\tau^2}\frac{\partial^2 \Phi}{\partial \phi^2} |
\frac{1}{\sigma^2\tau^2}\frac{\partial^2 \Phi}{\partial \phi^2} |
||
</math>。 |
</math> 。 |
||
其它微分算子,像<math>\nabla \cdot \mathbf{F}</math>,<math>\nabla \times \mathbf{F}</math>,都可以用<math>(\sigma,\ \tau,\ \phi)</math>坐標表示,只要將標度因子代入在[[正交坐標系]]條目內的一般公式。 |
其它微分算子,像 <math>\nabla \cdot \mathbf{F}</math> , <math>\nabla \times \mathbf{F}</math> ,都可以用 <math>(\sigma,\ \tau,\ \phi)</math> 坐標表示,只要將標度因子代入在[[正交坐標系]] 條目內的一般公式。 |
||
==第二種表述== |
==第二種表述== |
||
另外還有一種拋物線坐標系的表述,專門用於[[哈密頓-亞可比方程式]]。假若使用此種表述的公式,則哈密頓-亞可比方程式可以很容易的分解出來。應用此方法,可以導引出[[拉普拉斯-龍格-冷次向量#哈密頓- |
另外還有一種拋物線坐標系的表述,專門用於[[哈密頓-亞可比方程式]]。假若使用此種表述的公式,則哈密頓-亞可比方程式可以很容易的分解出來。應用此方法,可以導引出[[拉普拉斯-龍格-冷次向量#哈密頓-雅可比方程式|拉普拉斯-龍格-冷次向量]]的恆定性. |
||
採用下述從拋物線坐標變換至直角坐標的公式: |
採用下述從拋物線坐標變換至直角坐標的公式: |
||
:<math> \eta ={ - z+\sqrt{x^2+y^2+z^2}}</math>、 |
:<math> \eta ={ - z+\sqrt{x^2+y^2+z^2}}</math> 、 |
||
:<math> \xi ={z+\sqrt{x^2+y^2+z^2}}</math>、 |
:<math> \xi ={z+\sqrt{x^2+y^2+z^2}}</math> 、 |
||
:<math> \phi =\arctan {y \over x}</math>。 |
:<math> \phi =\arctan {y \over x}</math> 。 |
||
假若<math>\phi=0</math>,則可得到一片截面;其坐標被限制於<math>x\ge 0</math>的 +xz-半平面: |
假若 <math>\phi=0</math> ,則可得到一片截面;其坐標被限制於 <math>x\ge 0</math> 的 +xz-半平面: |
||
:<math> \eta = - z + \sqrt{ x^2 + z^2}</math>、 |
:<math> \eta = - z + \sqrt{ x^2 + z^2}</math> 、 |
||
:<math> \xi =z + \sqrt{ x^2 + z^2}</math>。 |
:<math> \xi =z + \sqrt{ x^2 + z^2}</math> 。 |
||
假若包含於一條曲線的每一點的坐標<math>\eta</math>是一個常數,<math>\eta=c</math>,則 |
假若包含於一條曲線的每一點的坐標 <math>\eta</math> 是一個常數,<math>\eta=c</math> ,則 |
||
:<math> \left. z \right|_{\eta = c} = {x^2 \over 2 c} - {c \over 2}</math>。 |
:<math> \left. z \right|_{\eta = c} = {x^2 \over 2 c} - {c \over 2}</math> 。 |
||
這是一個共焦點在原點的拋物線;對稱軸與z-軸同軸;凹性向上。 |
這是一個共焦點在原點的拋物線;對稱軸與 z-軸同軸;凹性向上。 |
||
假若包含於一條曲線的每一點的坐標<math>\xi</math>是一個常數,<math>\xi=b</math>,則 |
假若包含於一條曲線的每一點的坐標 <math>\xi</math> 是一個常數,<math>\xi=b</math> ,則 |
||
:<math> \left. z \right|_{\xi = b} = {b \over 2} - {x^2 \over 2 b}</math>。 |
:<math> \left. z \right|_{\xi = b} = {b \over 2} - {x^2 \over 2 b}</math> 。 |
||
這也是一個共焦點在原點的拋物線;對稱軸與z-軸同軸;凹性向下。 |
這也是一個共焦點在原點的拋物線;對稱軸與 z-軸同軸;凹性向下。 |
||
思考任何一條向上的拋物線<math>\eta=c</math>與任何一條向下的拋物線<math>\xi=b</math>,我們想要求得兩條曲線的相交點: |
思考任何一條向上的拋物線 <math>\eta=c</math> 與任何一條向下的拋物線 <math>\xi=b</math> ,我們想要求得兩條曲線的相交點: |
||
:<math> {x^2 \over 2 c} - {c \over 2} = {b \over 2} - {x^2 \over 2 b}</math>。 |
:<math> {x^2 \over 2 c} - {c \over 2} = {b \over 2} - {x^2 \over 2 b}</math> 。 |
||
稍微計算,可得 |
稍微計算,可得 |
||
:<math>x=\sqrt{bc}</math>。 |
:<math>x=\sqrt{bc}</math> 。 |
||
將相交點的横坐標<math>x</math>代入向上的拋物線的公式, |
將相交點的横坐標 <math>x</math> 代入向上的拋物線的公式, |
||
:<math>z_c= {bc\over 2 c} - {c \over 2} = {b - c \over 2}</math>。 |
:<math>z_c= {bc\over 2 c} - {c \over 2} = {b - c \over 2}</math> 。 |
||
所以,相交點P坐標為<math>\left(\sqrt{bc},\ {b - c \over 2}\right)</math>。 |
所以,相交點 P 坐標為 <math>\left(\sqrt{bc},\ {b - c \over 2}\right)</math> 。 |
||
思考正切這兩條拋物線於點P的一對切線。向上的拋物線的切線的斜率為 |
思考正切這兩條拋物線於點 P 的一對切線。向上的拋物線的切線的斜率為 |
||
:<math>\frac{dz_c}{dx}=\frac{x}{c}=\sqrt{\frac{b}{c}}=s_c</math>。 |
:<math>\frac{dz_c}{dx}=\frac{x}{c}=\sqrt{\frac{b}{c}}=s_c</math> 。 |
||
向下的拋物線的切線的斜率為 |
向下的拋物線的切線的斜率為 |
||
:<math>{dz_b\over dx}= - {x \over b}= - \sqrt{c\over b}= s_b</math>。 |
:<math>{dz_b\over dx}= - {x \over b}= - \sqrt{c\over b}= s_b</math> 。 |
||
兩個斜率的乘積為 |
兩個斜率的乘積為 |
||
:<math>s_c s_b= - 1</math>。 |
:<math>s_c s_b= - 1</math> 。 |
||
所以,兩條切線相垂直。對於任何兩條凹性相反的拋物線,都會有同樣的結果。 |
所以,兩條切線相垂直。對於任何兩條凹性相反的拋物線,都會有同樣的結果。 |
||
假設<math>\phi\ne 0</math>。讓<math>\phi</math>值從<math>0</math>緩慢增值,這半平面會相應地繞著z-軸按照[[右手定則]]旋轉;拋物線坐標為常數的拋物線形成了拋物曲面。一對相反的拋物曲面的相交設定了一個圓圈。而<math>\phi</math>值設定的半平面,切過這圓圈於一個唯一點。這唯一點的直角坐標是<ref name="Menzel">{{cite book |last=Menzel|first=Donald H.|title=Mathematical Physics|year=1961| location=United States of America | publisher=Dover Publications| isbn=978-0486600567 | language=en| pages=pp. 139}}</ref>: |
假設 <math>\phi\ne 0</math> 。讓 <math>\phi</math> 值從 <math>0</math> 緩慢增值,這半平面會相應地繞著 z-軸按照[[右手定則]]旋轉;拋物線坐標為常數的拋物線 形成了拋物曲面。一對相反的拋物曲面的相交 設定了一個圓圈。而 <math>\phi</math> 值設定的半平面,切過這圓圈於一個唯一點。這唯一點的直角坐標是<ref name="Menzel">{{cite book |last=Menzel|first=Donald H.|title=Mathematical Physics|url=https://archive.org/details/mathematicalphys0000menz|year=1961| location=United States of America | publisher=Dover Publications| isbn=978-0486600567 | language=en| pages=pp. 139}}</ref>: |
||
:<math> x = \sqrt{\eta\xi}\ \cos \phi</math>、 |
:<math> x = \sqrt{\eta\xi}\ \cos \phi</math> 、 |
||
:<math> y = \sqrt{\eta\xi}\ \sin \phi</math>、 |
:<math> y = \sqrt{\eta\xi}\ \sin \phi</math> 、 |
||
:<math> z =\frac{1}{2}(\xi - \eta)</math>。 |
:<math> z =\frac{1}{2}(\xi - \eta)</math> 。 |
||
{{正交坐標系}} |
{{正交坐標系}} |
||
2023年12月25日 (一) 08:35的最新版本

拋物線坐標系(英語:Parabolic coordinates)是一種二維正交坐標系,兩個坐標的等值曲線都是共焦的拋物線。將二維的拋物線坐標系繞著拋物線的對稱軸旋轉,則可以得到三維的拋物線坐標系。
實際上,拋物線坐標可以應用在許多物理問題。例如,斯塔克效應(Stark effect),物體邊緣的位勢論,以及拉普拉斯-龍格-冷次向量的保守性。
二維拋物線坐標系
[编辑]直角坐標 可以用二維拋物線坐標 表示為
- 、
- ;
其中, , 。
反算回來,二維拋物線坐標 可以用直角坐標 表示為
- 、
- 。
坐標 為常數的曲線形成共焦的,凹性向上的(往 +y-軸)拋物線:
- ,
而坐標 為常數的曲線形成共焦的,凹性向下的(往 -y-軸)拋物線:
- 。
這些拋物線的焦點的位置都在原點。
二維標度因子
[编辑]拋物線坐標 的標度因子相等:
- 。
因此,面積的無窮小元素是
- 。
- 。
其它微分算子,像 , ,都可以用 坐標表示,只要將標度因子代入在正交坐標系條目內的一般公式。
三維拋物線坐標系
[编辑]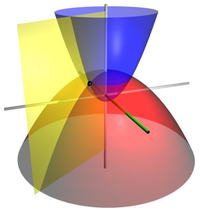
將二維的拋物線坐標系繞著拋物線的對稱軸旋轉,則可以得到三維的拋物線坐標系,又稱為旋轉拋物線坐標系。將對稱軸與 z-軸排列成同直線;而拋物線坐標系的共焦點與直角坐標系的原點同地點。直角坐標 可以用三維拋物線坐標 表示為
- 、
- 、
- ;
其中, , ,方位角 定義為
- 。
反算回來,三維拋物線坐標 可以用直角坐標 表示為
- 、
- 、
- 。
每一個 -坐標曲面都是共焦的,凹性向上的(往 +z-軸)拋物曲面:
- ,
而每一個 >-坐標曲面都是共焦的,凹性向下的(往 -z-軸)拋物曲面:
- 。
這些拋物曲面的焦點的位置都在原點。
三維標度因子
[编辑]三維標度因子為:
- 、
- 、
- 。
我們可以觀察出,標度因子 , 與二維標度因子相同。因此,體積的無窮小元素是
- 。
- 。
其它微分算子,像 , ,都可以用 坐標表示,只要將標度因子代入在正交坐標系 條目內的一般公式。
第二種表述
[编辑]另外還有一種拋物線坐標系的表述,專門用於哈密頓-亞可比方程式。假若使用此種表述的公式,則哈密頓-亞可比方程式可以很容易的分解出來。應用此方法,可以導引出拉普拉斯-龍格-冷次向量的恆定性.
採用下述從拋物線坐標變換至直角坐標的公式:
- 、
- 、
- 。
假若 ,則可得到一片截面;其坐標被限制於 的 +xz-半平面:
- 、
- 。
假若包含於一條曲線的每一點的坐標 是一個常數, ,則
- 。
這是一個共焦點在原點的拋物線;對稱軸與 z-軸同軸;凹性向上。
假若包含於一條曲線的每一點的坐標 是一個常數, ,則
- 。
這也是一個共焦點在原點的拋物線;對稱軸與 z-軸同軸;凹性向下。
思考任何一條向上的拋物線 與任何一條向下的拋物線 ,我們想要求得兩條曲線的相交點:
- 。
稍微計算,可得
- 。
將相交點的横坐標 代入向上的拋物線的公式,
- 。
所以,相交點 P 坐標為 。
思考正切這兩條拋物線於點 P 的一對切線。向上的拋物線的切線的斜率為
- 。
向下的拋物線的切線的斜率為
- 。
兩個斜率的乘積為
- 。
所以,兩條切線相垂直。對於任何兩條凹性相反的拋物線,都會有同樣的結果。
假設 。讓 值從 緩慢增值,這半平面會相應地繞著 z-軸按照右手定則旋轉;拋物線坐標為常數的拋物線 形成了拋物曲面。一對相反的拋物曲面的相交 設定了一個圓圈。而 值設定的半平面,切過這圓圈於一個唯一點。這唯一點的直角坐標是[1]:
- 、
- 、
- 。
參考文獻
[编辑]- Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 660. ISBN 0-07-043316-X.
- Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 185–186.
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 180.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 96.
- Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9.
- Moon P, Spencer DE. Parabolic Coordinates (μ, ν, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 34–36 (Table 1.08). ISBN 978-0387184302.
- ^ Menzel, Donald H. Mathematical Physics. United States of America: Dover Publications. 1961: pp. 139. ISBN 978-0486600567 (英语).








































![{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/0de55bf6476e43e24c58491488f09964454617bd)

























