(未显示5个用户的5个中间版本)
第12行:
第12行:
[[負數]]的平方根在[[複數 (數學)|複數系]]中有定義。而實際上,對任何定義了開平方運算的[[數學物件]]都可考慮其“平方根”(例如[[矩陣的平方根]])。
[[負數]]的平方根在[[複數 (數學)|複數系]]中有定義。而實際上,對任何定義了開平方運算的[[數學物件]]都可考慮其“平方根”(例如[[矩陣的平方根]])。
*MS的Excel中和大部分程式語言以 "sqrt()"表示。
*在MicroSoft 的試算表軟體 Excel與 大部分程式語言中 以 "sqrt()"表示求主平方根 。
== 历史 ==
== 历史 ==
耶鲁大学的巴比伦藏品[[YBC 7289]]是一块泥板,制作于[[前1800年]]到[[前1600年]]之间。泥板上是一个画了两条对角线正方形,标注了<math>\sqrt 2</math>的[[六十进制]]数字 1;24,51,10。<ref>{{cite web|url=http://www.math.ubc.ca/~cass/Euclid/ybc/analysis.html|title=Analysis of YBC 7289|work=ubc.ca|accessdate=19 January 2015|archive-date=2020-03-12|archive-url=https://web.archive.org/web/20200312005425/http://www.math.ubc.ca/~cass/Euclid/ybc/analysis.html|dead-url=yes}}</ref>十六进制的 1;24,51,10 即十进制的 1.41421296,精确到了小数点后5位(1.41421356...)。
耶鲁大学的巴比伦藏品[[YBC 7289]]是一块泥板,制作于[[前1800年]]到[[前1600年]]之间。泥板上是一个画了两条对角线正方形,标注了<math>\sqrt 2</math>的[[六十进制]]数字 1;24,51,10。<ref>{{cite web|url=http://www.math.ubc.ca/~cass/Euclid/ybc/analysis.html|title=Analysis of YBC 7289|work=ubc.ca|accessdate=19 January 2015|archive-date=2020-03-12|archive-url=https://web.archive.org/web/20200312005425/http://www.math.ubc.ca/~cass/Euclid/ybc/analysis.html|dead-url=yes}}</ref>六十 进制的 1;24,51,10 即十进制的 1.41421296,精确到了小数点后5位(1.41421356...)。
[[莱因德数学纸草书]]大约成书于[[前1650年]],内容抄写自更早年代的教科书。书中展示了埃及人使用反比法求平方根的过程。<ref>Anglin, W.S. (1994). ''Mathematics: A Concise History and Philosophy''. New York: Springer-Verlag.</ref>
[[莱因德数学纸草书]]大约成书于[[前1650年]],内容抄写自更早年代的教科书。书中展示了埃及人使用反比法求平方根的过程。<ref>Anglin, W.S. (1994). ''Mathematics: A Concise History and Philosophy''. New York: Springer-Verlag.</ref>
第41行:
第41行:
最有影響的是拉丁語的{{Lang-la|radix|label=none}}(平方根),1220年Leconardo在《''{{Lang-la|Practica geometriae|label=none}}''》中使用℞(R右下角的有一斜劃,像P和x的合體);⎷(沒有上面的橫劃)是由[[克里斯多福·魯登道夫]]在1525年的書''Coss''首次使用,據說是小寫r的變型;后来数学家[[笛卡尔]]给其加上线括号,但与前面的方根符号是分开的(即“⎷‾”),因此在复杂的式子中它显得很乱。直至18世纪中叶,数学家卢贝将前面的方根符号与线括号一笔写成,并将[[根指数]]写在[[根号]]的左上角,以表示高次方根(当根指数为2时,省略不写),从而形成了现在人們熟知的[[开方]][[运算]]符号<math>\sqrt[n]{\,\,}</math>。
最有影響的是拉丁語的{{Lang-la|radix|label=none}}(平方根),1220年Leconardo在《''{{Lang-la|Practica geometriae|label=none}}''》中使用℞(R右下角的有一斜劃,像P和x的合體);⎷(沒有上面的橫劃)是由[[克里斯多福·魯登道夫]]在1525年的書''Coss''首次使用,據說是小寫r的變型;后来数学家[[笛卡尔]]给其加上线括号,但与前面的方根符号是分开的(即“⎷‾”),因此在复杂的式子中它显得很乱。直至18世纪中叶,数学家卢贝将前面的方根符号与线括号一笔写成,并将[[根指数]]写在[[根号]]的左上角,以表示高次方根(当根指数为2时,省略不写),从而形成了现在人們熟知的[[开方]][[运算]]符号<math>\sqrt[n]{\,\,}</math>。
== 實數 ==
== 正 數 ==
⚫ [[File:Square root 0 25.svg|thumb|400px|函數<math>f(x) = \sqrt x</math>圖,半[[拋物線]]與垂直準線。]]
<math>x</math>的平方根亦可用[[指數]]表示,如:
<math>x</math>的平方根亦可用[[指數]]表示,如:
:<math>x^\frac 1 2 = \sqrt x</math>
:<math>x^\frac 1 2 = \sqrt x</math>
第51行:
第53行:
\end{cases}\right)</math>
\end{cases}\right)</math>
=== 正數 ===
⚫ [[File:Square root 0 25.svg|thumb|400px|函數<math>f(x) = \sqrt x</math>圖,半[[拋物線]]與垂直準線。]]
若正[[整數]]<math>x</math>是[[平方數]],則其平方根是整數。若正整數<math>x</math>不是平方數,則其平方根是[[無理數]]。
若正[[整數]]<math>x</math>是[[平方數]],則其平方根是整數。若正整數<math>x</math>不是平方數,則其平方根是[[無理數]]。
第62行:
第62行:
\end{align}</math>
\end{align}</math>
=== 負數 ===
== 负数与複 數 ==
⚫ 正数和负数的平方都是正数,0的平方是0,因此负数没有[[实数]]平方根。然而,我们可以把我们所使用的数字集合扩大,加入负数的平方根,这样的集合就是[[複數 (數學)|複數]]。首先需要引入一个实数集之外的新数字,记作<math>i</math>(也可以记作<math>j</math>,比如[[电学]]场景中<math>i</math>一般表示电流),称之为[[虚数单位]],定义即为<math>i^2 = -1</math>,故<math>i</math>是-1的平方根,而且<math>(-i)^2 = i^2 = -1</math>,所以<math>-i</math>也是-1的平方根。通常称-1的算术平方根是<math>i</math>,如果<math>x</math>是任意非负实数,则<math>-x</math>的算术平方根就是:
[[負數]]的平方根在[[複數 (數學)|複數]]範圍内同樣有定義。
⚫ :<math>\sqrt{-x} = i \sqrt{x}</math>
负数有兩個平方根,它们为一对[[共軛複數|共轭]]的[[虚数|纯虚数]]。
例如-5的 平方根有两个 ,它们分别 为<math>\sqrt{5}i</math>和<math>-\sqrt{5}i</math> 。
以[[虛數單位]]<math>i=\sqrt{-1}</math>可將負數<math>x</math>的平方根表示為
之所 以等式右侧(包括其对应的负值)是 <math>-x</math>的算术 平方根,是因为:
⚫ :<math>(i\sqrt{x})^2 = i^2(\sqrt{x})^2 = (-1)x = -x</math>
负数的兩個平方根为一对[[共軛複數|共轭]]的[[虚数|纯虚数]]。
:<math>\pm \sqrt{-x}i</math>,其中<math>\sqrt{-x}i = \sqrt x</math>。
例如-5的平方根有两个,它们分别为<math>\sqrt{5}i</math>和<math>-\sqrt{5}i</math>。
對於負數<math>x</math>、<math>y</math>,以下式成立:
對於負數<math>x</math>、<math>y</math>,以下式成立:
第79行:
第79行:
\frac{\sqrt{x}}{\sqrt{y}} &= \frac{\sqrt{-x}i}{\sqrt{-y}i} = \sqrt{\frac{-x}{-y}} = \sqrt{\frac{x}{y}}
\frac{\sqrt{x}}{\sqrt{y}} &= \frac{\sqrt{-x}i}{\sqrt{-y}i} = \sqrt{\frac{-x}{-y}} = \sqrt{\frac{x}{y}}
\end{align}</math>
\end{align}</math>
== 负数与複數 ==
⚫ 正数和负数的平方都是正数,0的平方是0,因此负数没有[[实数]]平方根。然而,我们可以把我们所使用的数字集合扩大,加入负数的平方根,这样的集合就是[[複數 (數學)|複數]]。首先需要引入一个实数集之外的新数字,记作<math>i</math>(也可以记作<math>j</math>,比如[[电学]]场景中<math>i</math>一般表示电流),称之为[[虚数单位]],定义即为<math>i^2 = -1</math>,故<math>i</math>是-1的平方根,而且<math>(-i)^2 = i^2 = -1</math>,所以<math>-i</math>也是-1的平方根。通常称-1的算术平方根是<math>i</math>,如果<math>x</math>是任意非负实数,则<math>-x</math>的算术平方根就是:
⚫ :<math>\sqrt{-x} = i \sqrt{x}</math>
之所以等式右侧(包括其对应的负值)是<math>-x</math>的算术平方根,是因为:
⚫ :<math>(i\sqrt{x})^2 = i^2(\sqrt{x})^2 = (-1)x = -x</math>
⚫ 对于任何一个非零的复数<math>z</math>都存在两个複数<math>w</math>使得<math>w^2 = z</math>。
=== 虚数的算术平方根 ===
=== 虚数的算术平方根 ===
第132行:
第123行:
=== 复数的算术平方根 ===
=== 复数的算术平方根 ===
[[Image:Visualisation_complex_number_roots.svg|right|thumb|极坐标下,复数<math>z</math>的几个方根]]
[[Image:Visualisation_complex_number_roots.svg|right|thumb|极坐标下,复数<math>z</math>的几个方根]]
⚫ 对于任何一个非零的复数<math>z</math>都存在两个複数<math>w</math>使得<math>w^2 = z</math>。
首先,我们将复数<math>x + iy</math> 看作是平面上的点,即[[笛卡尔坐标系]]中的<math>(x, y)</math>点。这个点也可以写作[[极坐标]]的<math>(r, \varphi)</math>,其中<math>r \geq 0</math>,是该点到坐标原点的距离,<math>\varphi</math>则是从原点到该点的直线与实数坐标轴(<math>x</math>轴)的夹角。[[复分析]]中,通常把该点记作<math>re^{i \varphi}</math>。如果
首先,我们将复数<math>x + iy</math> 看作是平面上的点,即[[笛卡尔坐标系]]中的<math>(x, y)</math>点。这个点也可以写作[[极坐标]]的<math>(r, \varphi)</math>,其中<math>r \geq 0</math>,是该点到坐标原点的距离,<math>\varphi</math>则是从原点到该点的直线与实数坐标轴(<math>x</math>轴)的夹角。[[复分析]]中,通常把该点记作<math>re^{i \varphi}</math>。如果
第339行:
第332行:
===巴比倫方法===
===巴比倫方法===
<div class="rellink<nowiki> </nowiki>noprint relarticle mainarticle">主条目:{{link-en|巴比倫方法|Babylonian method}}</div>
{{main| {{link-en|巴比倫方法|Babylonian method}}}}
巴比伦求平方根的算法实际上很简单:(假设要求一个数N的平方根)
巴比伦求平方根的算法实际上很简单:(假设要求一个数N的平方根)
算术平方根的數學表示式 在數學 中,一個數
x
{\displaystyle x}
平方根
y
{\displaystyle y}
y
2
=
x
{\displaystyle y^{2}=x}
平方 結果等於
x
{\displaystyle x}
4
2
=
(
−
4
)
2
=
16
{\displaystyle 4^{2}=(-4)^{2}=16}
任意非負實數
x
{\displaystyle x}
算术平方根 或主平方根 (英語:principal square root ),記為
x
{\displaystyle {\sqrt {x}}}
{\displaystyle {\sqrt {\quad }}}
根号 。例如,9的算术平方根为3,记作
9
=
3
{\displaystyle {\sqrt {9}}=3}
3
2
=
3
×
3
=
9
{\displaystyle 3^{2}=3\times 3=9}
被开方数 (英語:radicand ),是根号下的数字或者表达式,即例子中的数字9。
正数
x
{\displaystyle x}
相反数 的平方根:正数
x
{\displaystyle {\sqrt {x}}}
−
x
{\displaystyle -{\sqrt {x}}}
±
x
{\displaystyle \pm {\sqrt {x}}}
負數 的平方根在複數系 中有定義。而實際上,對任何定義了開平方運算的數學物件 都可考慮其“平方根”(例如矩陣的平方根 )。
在MicroSoft的試算表軟體Excel與大部分程式語言中以 "sqrt()"表示求主平方根。 耶鲁大学的巴比伦藏品YBC 7289 是一块泥板,制作于前1800年 到前1600年 之间。泥板上是一个画了两条对角线正方形,标注了
2
{\displaystyle {\sqrt {2}}}
六十进制 数字 1;24,51,10。[ 1]
莱因德数学纸草书 大约成书于前1650年 ,内容抄写自更早年代的教科书。书中展示了埃及人使用反比法求平方根的过程。[ 2]
古印度 的《绳法经 》大约成书于前800年 到前500年 之间,书中记载了将2的平方根的计算精确到小数点后5位的方法。
古希腊的《几何原本 》大约成书于前380年 ,书中还阐述了如果正整数 不是完全平方数 ,那么它的平方根就一定是无理数 ——一种无法以两个整数的比值 表示的数(无法写作m/n ,其中m 和n 是整数)。[ 3]
中国的《书 》成书于汉朝 (约前202年 到前186年 之间),书中介绍了使用盈不足术 求平方根的方法。
古代未有劃一的平方根符號時,人們通常使用他們語言內開方這個字的首個字母的變型作為開方號。
中世紀時,拉丁語 中的latus (正方形邊)的首個字母“L”被不少歐洲人採用;亨利·布里格斯 在其著作《Arithmetica Logarithmica 》中則用橫線當成latus 的簡寫,在被開方的數下畫一線。
最有影響的是拉丁語的radix (平方根),1220年Leconardo在《Practica geometriae 克里斯多福·魯登道夫 在1525年的書Coss 首次使用,據說是小寫r的變型;后来数学家笛卡尔 给其加上线括号,但与前面的方根符号是分开的(即“⎷‾”),因此在复杂的式子中它显得很乱。直至18世纪中叶,数学家卢贝将前面的方根符号与线括号一笔写成,并将根指数 写在根号 的左上角,以表示高次方根(当根指数为2时,省略不写),从而形成了现在人們熟知的开方 运算 符号
n
{\displaystyle {\sqrt[{n}]{\,\,}}}
函數
f
(
x
)
=
x
{\displaystyle f(x)={\sqrt {x}}}
拋物線 與垂直準線。
x
{\displaystyle x}
指數 表示,如:
x
1
2
=
x
{\displaystyle x^{\frac {1}{2}}={\sqrt {x}}}
x
{\displaystyle x}
絕對值 可用
x
2
{\displaystyle x^{2}}
|
x
|
=
x
2
(
=
{
x
(
x
≥
0
)
−
x
(
x
<
0
)
)
{\displaystyle |x|={\sqrt {x^{2}}}\left(={\begin{cases}x&(x\geq 0)\\-x&(x<0)\end{cases}}\right)}
若正整數
x
{\displaystyle x}
平方數 ,則其平方根是整數。若正整數
x
{\displaystyle x}
無理數 。
對於正數
x
{\displaystyle x}
y
{\displaystyle y}
x
y
=
x
y
x
y
=
x
y
{\displaystyle {\begin{aligned}{\sqrt {x}}{\sqrt {y}}&={\sqrt {xy}}\\{\frac {\sqrt {x}}{\sqrt {y}}}&={\sqrt {\frac {x}{y}}}\end{aligned}}}
正数和负数的平方都是正数,0的平方是0,因此负数没有实数 平方根。然而,我们可以把我们所使用的数字集合扩大,加入负数的平方根,这样的集合就是複數 。首先需要引入一个实数集之外的新数字,记作
i
{\displaystyle i}
j
{\displaystyle j}
电学 场景中
i
{\displaystyle i}
虚数单位 ,定义即为
i
2
=
−
1
{\displaystyle i^{2}=-1}
i
{\displaystyle i}
(
−
i
)
2
=
i
2
=
−
1
{\displaystyle (-i)^{2}=i^{2}=-1}
−
i
{\displaystyle -i}
i
{\displaystyle i}
x
{\displaystyle x}
−
x
{\displaystyle -x}
−
x
=
i
x
{\displaystyle {\sqrt {-x}}=i{\sqrt {x}}}
例如-5的平方根有两个,它们分别为
5
i
{\displaystyle {\sqrt {5}}i}
−
5
i
{\displaystyle -{\sqrt {5}}i}
之所以等式右侧(包括其对应的负值)是
−
x
{\displaystyle -x}
(
i
x
)
2
=
i
2
(
x
)
2
=
(
−
1
)
x
=
−
x
{\displaystyle (i{\sqrt {x}})^{2}=i^{2}({\sqrt {x}})^{2}=(-1)x=-x}
负数的兩個平方根为一对共轭 的纯虚数 。
對於負數
x
{\displaystyle x}
y
{\displaystyle y}
x
y
=
−
x
i
×
−
y
i
=
x
y
i
2
=
−
x
y
x
y
=
−
x
i
−
y
i
=
−
x
−
y
=
x
y
{\displaystyle {\begin{aligned}{\sqrt {x}}{\sqrt {y}}&={\sqrt {-x}}\,i\times {\sqrt {-y}}\,i={\sqrt {xy}}\,i^{2}=-{\sqrt {xy}}\\{\frac {\sqrt {x}}{\sqrt {y}}}&={\frac {{\sqrt {-x}}i}{{\sqrt {-y}}i}}={\sqrt {\frac {-x}{-y}}}={\sqrt {\frac {x}{y}}}\end{aligned}}}
复数平面中,
i
{\displaystyle i}
虚数
i
{\displaystyle i}
i
=
2
2
+
i
2
2
=
2
2
(
1
+
i
)
{\displaystyle {\sqrt {i}}={\frac {\sqrt {2}}{2}}+i{\frac {\sqrt {2}}{2}}={\frac {\sqrt {2}}{2}}(1+i)}
这个公式可以通过用代数 方法推导,只需找到特定的实数
a
{\displaystyle a}
b
{\displaystyle b}
i
=
(
a
+
b
i
)
2
=
a
2
+
2
a
b
i
−
b
2
{\displaystyle {\begin{aligned}i&=(a+bi)^{2}\\&=a^{2}+2abi-b^{2}\end{aligned}}}
就可以得到方程组
{
2
a
b
=
1
a
2
−
b
2
=
0
{\displaystyle {\begin{cases}2ab=1\\a^{2}-b^{2}=0\end{cases}}}
的解:
a
=
b
=
±
2
2
{\displaystyle a=b=\pm {\frac {\sqrt {2}}{2}}}
其中,算术平方根即为
a
=
b
=
2
2
{\displaystyle a=b={\frac {\sqrt {2}}{2}}}
这个公式还可以通过棣莫弗公式 得到,设
i
=
cos
(
π
2
)
+
i
sin
(
π
2
)
{\displaystyle i=\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)}
就可以推出
i
=
[
cos
(
π
2
)
+
i
sin
(
π
2
)
]
1
2
=
cos
(
π
4
)
+
i
sin
(
π
4
)
=
2
2
+
i
2
2
=
2
2
(
1
+
i
)
{\displaystyle {\begin{aligned}{\sqrt {i}}&=\left[\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)\right]^{\frac {1}{2}}\\&=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)\\&={\frac {\sqrt {2}}{2}}+i{\frac {\sqrt {2}}{2}}\\&={\frac {\sqrt {2}}{2}}(1+i)\end{aligned}}}
极坐标下,复数
z
{\displaystyle z}
对于任何一个非零的复数
z
{\displaystyle z}
w
{\displaystyle w}
w
2
=
z
{\displaystyle w^{2}=z}
首先,我们将复数
x
+
i
y
{\displaystyle x+iy}
笛卡尔坐标系 中的
(
x
,
y
)
{\displaystyle (x,y)}
极坐标 的
(
r
,
φ
)
{\displaystyle (r,\varphi )}
r
≥
0
{\displaystyle r\geq 0}
φ
{\displaystyle \varphi }
x
{\displaystyle x}
复分析 中,通常把该点记作
r
e
i
φ
{\displaystyle re^{i\varphi }}
z
=
r
e
i
φ
,
−
π
<
φ
≤
π
{\displaystyle z=re^{i\varphi },-\pi <\varphi \leq \pi }
那么我们将
z
{\displaystyle z}
z
=
r
e
i
φ
2
{\displaystyle {\sqrt {z}}={\sqrt {r}}e^{\frac {i\varphi }{2}}}
因此,平方根函数除了在非正实数轴上以外是处处全纯 的。
1
+
x
{\displaystyle {\sqrt {1+x}}}
x
(
|
x
|
<
1
)
{\displaystyle x(\left\vert x\right\vert <1)}
上面的公式还可以用三角函数 的形式表达:
r
(
cos
φ
+
i
sin
φ
)
=
r
(
cos
φ
2
+
i
sin
φ
2
)
{\displaystyle {\sqrt {r\left(\cos \varphi +i\sin \varphi \right)}}={\sqrt {r}}\left(\cos {\frac {\varphi }{2}}+i\sin {\frac {\varphi }{2}}\right)}
如果使用笛卡尔坐标的形式表达复数 z ,其算术平方根可以使用如下公式:[ 4] [ 5]
z
=
|
z
|
+
ℜ
(
z
)
2
±
i
|
z
|
−
ℜ
(
z
)
2
{\displaystyle {\sqrt {z}}={\sqrt {\frac {|z|+\Re (z)}{2}}}\pm i{\sqrt {\frac {|z|-\Re (z)}{2}}}}
其中,方根虚部的符号 与被开方数虚部的符号相同(为0时取正);主值
在虛數裡,平方根函數的值不是連續的,以下等式不一定成立:
z
w
=
z
w
{\displaystyle {\sqrt {zw}}={\sqrt {z}}{\sqrt {w}}}
w
z
=
w
z
{\displaystyle {\frac {\sqrt {w}}{\sqrt {z}}}={\sqrt {\frac {w}{z}}}}
z
∗
=
(
z
)
∗
{\displaystyle {\sqrt {z^{*}}}=\left({\sqrt {z}}\right)^{*}}
所以這是錯誤的:
−
1
=
i
⋅
i
=
−
1
⋅
−
1
=
(
−
1
)
⋅
(
−
1
)
=
1
=
1
{\displaystyle -1=i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)\cdot (-1)}}={\sqrt {1}}=1}
例:若
x
∈
R
{\displaystyle x\in \mathbb {R} }
x
4
+
2
x
2
+
1
=
(
x
2
+
1
)
2
=
|
x
2
+
1
|
=
x
2
+
1
{\displaystyle {\sqrt {x^{4}+2x^{2}+1}}={\sqrt {(x^{2}+1)^{2}}}=|x^{2}+1|=x^{2}+1\,\!}
數學史中,最重要的平方根可以說是
2
{\displaystyle {\sqrt {2}}}
正方形 的對角線 長,是第一個公認的無理數 ,也叫毕达哥拉斯常数 ,其值到小數點14位約為1.4142135623731。
2
{\displaystyle {\sqrt {2}}}
歸謬法 證明:
設
2
{\displaystyle {\sqrt {2}}}
有理數 ,可表示為
p
q
{\displaystyle {\frac {p}{q}}}
p
{\displaystyle p}
q
{\displaystyle q}
互質 之正整數。
因為
(
2
)
2
=
p
2
q
2
=
2
{\displaystyle \left({\sqrt {2}}\right)^{2}={\frac {p^{2}}{q^{2}}}=2}
p
2
{\displaystyle p^{2}}
p
{\displaystyle p}
2
k
{\displaystyle 2k}
k
{\displaystyle k}
但是
2
q
2
=
p
2
=
4
k
2
{\displaystyle 2q^{2}=p^{2}=4k^{2}}
q
2
=
2
k
2
{\displaystyle q^{2}=2k^{2}}
q
2
{\displaystyle q^{2}}
q
{\displaystyle q}
依上兩式,
p
{\displaystyle p}
q
{\displaystyle q}
p
{\displaystyle p}
q
{\displaystyle q}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle {\sqrt {2}}}
24
=
2
2
⋅
6
=
2
2
6
=
2
6
{\displaystyle {\sqrt {24}}={\sqrt {2^{2}\cdot 6}}={\sqrt {2^{2}}}{\sqrt {6}}=2{\sqrt {6}}}
注意,6 的质因数分解为 2 × 3,不能写成某个数的平方,因此
2
6
{\displaystyle 2{\sqrt {6}}}
北宋贾宪增乘开平方法 《九章算术 》和《孙子算经 》都有筹算 的开方法。宋代 数学家贾宪 发明释锁开平方法 、增乘开平方法 ;明代 数学家王素文 ,程大位 发明珠算开平方法 ,而朱载堉 《算学新说 》首创用81位算盘 开方,精确到25位数字[ 6]
長除式算平方根的方式也稱為直式開方法,原理是
.
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
=
a
2
+
(
2
a
+
b
)
b
{\displaystyle .(a+b)^{2}=a^{2}+2ab+b^{2}=a^{2}+(2a+b)b}
首先將要開平方根的數從小數點分別向右及向左每兩個位一組分開,如98765.432內小數點前的65是一組,87是一組,9是一組,小數點後的43是一組,之後是單獨一個2,要補一個0而得20是一組。如1 04.85 73得四組,順序為1' 04. 85' 73'。
將最左的一組的數減去最接近又少於它的平方數,並將該平方數的開方(應該是個位數)記下。
將上一步所得之差乘100,和下一組數加起來。
將記下的數乘20,然後將它加上某個個位數,再乘以該個個位數,令這個積不大於但最接近上一步所得之差,並將該個個位數記下,且將上一步所得之差減去所得之積。
記下的數一次隔兩位記下。
重覆第3步,直到找到答案。
可以在數字的最右補上多組的00'以求得理想的精確度為止。 下面以
200
{\displaystyle {\sqrt {200}}}
1
4
.
1
4
2
2
|
00.00
|
00
|
00
1
_
1
×
1
≤
2
1
00
a
=
1
0
,
b
=
4
96
_
⇒
(
2
a
+
b
)
b
=
2
4
×
4
=
96
≤
100
4
00
a
=
1
4
0
,
b
=
1
2
81
_
⇒
(
2
a
+
b
)
b
=
28
1
×
1
=
281
≤
400
1
19
00
a
=
1
4
1
0
,
b
=
4
1
12
96
_
⇒
(
2
a
+
b
)
b
=
282
4
×
4
=
11296
≤
11900
6
04
00
a
=
1
4
1
4
0
,
b
=
2
5
65
64
_
⇒
(
2
a
+
b
)
b
=
2828
2
×
2
=
56564
≤
60400
38
36
{\displaystyle {\begin{array}{ll}\quad {\color {Red}1}~~{\color {Green}4}.~~{\color {Blue}1}~~{\color {Purple}4}~~{\color {Orange}2}\\{\sqrt {2|00.00|00|00}}\\\quad {\underline {1\quad ~}}&\quad {\color {Red}1}\times {\color {Red}1}\leq 2\\\quad 1~00&a={\color {Red}1}0,b={\color {Green}4}\\\quad {\underline {~~\,96\quad ~}}&\quad \Rightarrow (2a+b)b=2{\color {Green}4}\times {\color {Green}4}=96\leq 100\\\qquad ~4~00&a={\color {Red}1}{\color {Green}4}0,b={\color {Blue}1}\\\qquad ~{\underline {2~81\quad ~}}&\quad \Rightarrow (2a+b)b=28{\color {Blue}1}\times {\color {Blue}1}=281\leq 400\\\qquad ~1~19~00&a={\color {Red}1}{\color {Green}4}{\color {Blue}1}0,b={\color {Purple}4}\\\qquad ~{\underline {1~12~96\quad ~}}&\quad \Rightarrow (2a+b)b=282{\color {Purple}4}\times {\color {Purple}4}=11296\leq 11900\\\qquad \quad ~~6~04~00&a={\color {Red}1}{\color {Green}4}{\color {Blue}1}{\color {Purple}4}0,b={\color {Orange}2}\\\qquad \quad ~~{\underline {5~65~64}}&\quad \Rightarrow (2a+b)b=2828{\color {Orange}2}\times {\color {Orange}2}=56564\leq 60400\\\qquad \quad \quad ~\,38~36\\\end{array}}}
200
≈
14.14213562373095048801668872421
{\displaystyle {\sqrt {200}}\approx 14.14213562373095048801668872421}
四捨五入 得答案為14.14。
事實上,將算法稍作改動,可以開任何次方的根,詳見n次方算法 。
利用高精度长式除法可以计算出1至20的平方根如下:
1
{\displaystyle {\sqrt {1}}}
=
{\displaystyle =\,}
1
2
{\displaystyle {\sqrt {2}}}
≈
{\displaystyle \approx }
1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462
3
{\displaystyle {\sqrt {3}}}
≈
{\displaystyle \approx }
1.7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909
4
{\displaystyle {\sqrt {4}}}
=
{\displaystyle =\,}
2
5
{\displaystyle {\sqrt {5}}}
≈
{\displaystyle \approx }
2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638
6
{\displaystyle {\sqrt {6}}}
≈
{\displaystyle \approx }
2.4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457
7
{\displaystyle {\sqrt {7}}}
≈
{\displaystyle \approx }
2.6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230
8
{\displaystyle {\sqrt {8}}}
≈
{\displaystyle \approx }
2.8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924
9
{\displaystyle {\sqrt {9}}}
=
{\displaystyle =\,}
3
10
{\displaystyle {\sqrt {10}}}
≈
{\displaystyle \approx }
3.1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639
11
{\displaystyle {\sqrt {11}}}
≈
{\displaystyle \approx }
3.3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609
12
{\displaystyle {\sqrt {12}}}
≈
{\displaystyle \approx }
3.4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818
13
{\displaystyle {\sqrt {13}}}
≈
{\displaystyle \approx }
3.6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293
14
{\displaystyle {\sqrt {14}}}
≈
{\displaystyle \approx }
3.7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307
15
{\displaystyle {\sqrt {15}}}
≈
{\displaystyle \approx }
3.8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937
16
{\displaystyle {\sqrt {16}}}
=
{\displaystyle =\,}
4
17
{\displaystyle {\sqrt {17}}}
≈
{\displaystyle \approx }
4.1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338
18
{\displaystyle {\sqrt {18}}}
≈
{\displaystyle \approx }
4.2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386
19
{\displaystyle {\sqrt {19}}}
≈
{\displaystyle \approx }
4.3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203
20
{\displaystyle {\sqrt {20}}}
≈
{\displaystyle \approx }
4.4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276
如果要求
S
(
S
>
1
)
{\displaystyle S\,(S>1)}
1
<
x
0
<
S
{\displaystyle 1\,<\,x_{0}\,<\,S}
x
n
+
1
=
1
2
(
x
n
+
S
x
n
)
{\displaystyle x_{n+1}={\frac {1}{2}}\left(x_{n}+{\frac {S}{x_{n}}}\right)}
例子:求
125348
{\displaystyle {\sqrt {125348}}}
有效數字 。
x
0
=
3
6
=
729.000
{\displaystyle x_{0}=3^{6}=729.000\,\!}
x
1
=
1
2
(
x
0
+
S
x
0
)
=
1
2
(
729.000
+
125348
729.000
)
=
450.472
{\displaystyle x_{1}={\frac {1}{2}}\left(x_{0}+{\frac {S}{x_{0}}}\right)={\frac {1}{2}}\left(729.000+{\frac {125348}{729.000}}\right)=450.472}
x
2
=
1
2
(
x
1
+
S
x
1
)
=
1
2
(
450.472
+
125348
450.472
)
=
364.365
{\displaystyle x_{2}={\frac {1}{2}}\left(x_{1}+{\frac {S}{x_{1}}}\right)={\frac {1}{2}}\left(450.472+{\frac {125348}{450.472}}\right)=364.365}
x
3
=
1
2
(
x
2
+
S
x
2
)
=
1
2
(
364.365
+
125348
364.365
)
=
354.191
{\displaystyle x_{3}={\frac {1}{2}}\left(x_{2}+{\frac {S}{x_{2}}}\right)={\frac {1}{2}}\left(364.365+{\frac {125348}{364.365}}\right)=354.191}
x
4
=
1
2
(
x
3
+
S
x
3
)
=
1
2
(
354.191
+
125348
354.191
)
=
354.045
{\displaystyle x_{4}={\frac {1}{2}}\left(x_{3}+{\frac {S}{x_{3}}}\right)={\frac {1}{2}}\left(354.191+{\frac {125348}{354.191}}\right)=354.045}
x
5
=
1
2
(
x
4
+
S
x
4
)
=
1
2
(
354.045
+
125348
354.045
)
=
354.045
{\displaystyle x_{5}={\frac {1}{2}}\left(x_{4}+{\frac {S}{x_{4}}}\right)={\frac {1}{2}}\left(354.045+{\frac {125348}{354.045}}\right)=354.045}
因此
125348
≈
354.045
{\displaystyle {\sqrt {125348}}\approx 354.045}
平方根可以简便地用连分数的形式表示,关于连分数请见连分数 ,其中1至20的算术平方根分别可用连分数表示为:
1
=
1
{\displaystyle {\sqrt {1}}=1}
2
=
[
1
;
2
,
2
,
2
,
2...
]
{\displaystyle {\sqrt {2}}=[1;2,2,2,2...]}
3
=
[
1
;
1
,
2
,
1
,
2...
]
{\displaystyle {\sqrt {3}}=[1;1,2,1,2...]}
4
=
2
{\displaystyle {\sqrt {4}}=2}
5
=
[
2
;
4
,
4
,
4
,
4...
]
{\displaystyle {\sqrt {5}}=[2;4,4,4,4...]}
6
=
[
2
;
2
,
4
,
2
,
4...
]
{\displaystyle {\sqrt {6}}=[2;2,4,2,4...]}
7
=
[
2
;
1
,
1
,
1
,
4
,
1
,
1
,
1
,
4...
]
{\displaystyle {\sqrt {7}}=[2;1,1,1,4,1,1,1,4...]}
8
=
[
2
;
1
,
4
,
1
,
4...
]
{\displaystyle {\sqrt {8}}=[2;1,4,1,4...]}
9
=
3
{\displaystyle {\sqrt {9}}=3}
10
=
[
3
;
6
,
6
,
6
,
6...
]
{\displaystyle {\sqrt {10}}=[3;6,6,6,6...]}
11
=
[
3
;
3
,
6
,
3
,
6...
]
{\displaystyle {\sqrt {11}}=[3;3,6,3,6...]}
12
=
[
3
;
2
,
6
,
2
,
6...
]
{\displaystyle {\sqrt {12}}=[3;2,6,2,6...]}
13
=
[
3
;
1
,
1
,
1
,
1
,
6
,
1
,
1
,
1
,
1
,
6...
]
{\displaystyle {\sqrt {13}}=[3;1,1,1,1,6,1,1,1,1,6...]}
14
=
[
3
;
1
,
2
,
1
,
6
,
1
,
2
,
1
,
6...
]
{\displaystyle {\sqrt {14}}=[3;1,2,1,6,1,2,1,6...]}
15
=
[
3
;
1
,
6
,
1
,
6...
]
{\displaystyle {\sqrt {15}}=[3;1,6,1,6...]}
16
=
4
{\displaystyle {\sqrt {16}}=4}
17
=
[
4
;
8
,
8
,
8
,
8...
]
{\displaystyle {\sqrt {17}}=[4;8,8,8,8...]}
18
=
[
4
;
4
,
8
,
4
,
8...
]
{\displaystyle {\sqrt {18}}=[4;4,8,4,8...]}
19
=
[
4
;
2
,
1
,
3
,
1
,
2
,
8
,
2
,
1
,
3
,
1
,
2
,
8...
]
{\displaystyle {\sqrt {19}}=[4;2,1,3,1,2,8,2,1,3,1,2,8...]}
20
=
[
4
;
2
,
8
,
2
,
8...
]
{\displaystyle {\sqrt {20}}=[4;2,8,2,8...]}
连分数部分均循环,省略号前为2或4个循环节。
巴比伦求平方根的算法实际上很简单:(假设要求一个数N的平方根)
预测一个平方根
x
{\displaystyle x}
y
{\displaystyle y}
x
y
=
N
{\displaystyle xy=N}
求预测值与初始值的均值:
x
=
x
+
y
2
{\displaystyle x={\frac {x+y}{2}}}
y
=
N
x
{\displaystyle y={\frac {N}{x}}}
比较
x
{\displaystyle x}
y
{\displaystyle y}
這個方法是從佩爾方程 演變過來的,它通過不斷減去奇數來求得答案。
給定線段AB 和1,求一條長為
A
B
{\displaystyle {\sqrt {AB}}}
畫線AB ,延長BA 至C 使
A
C
=
1
{\displaystyle AC=1}
以BC 的中點為圓心,OC 為半徑畫圓
過A 畫BC 的垂直線,垂直線和圓弧交於D ,AD 即為所求之長度 將整個過程搬到直角座標 上,已知AC =1,設
O =
(
0
,
0
)
{\displaystyle (0,0)}
AB =
n
{\displaystyle n}
直徑為BC 的圓就是
x
2
+
y
2
=
(
n
+
1
2
)
2
{\displaystyle x^{2}+y^{2}=\left({\frac {n+1}{2}}\right)^{2}}
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
r
{\displaystyle r}
將
(
n
+
1
2
−
1
)
{\displaystyle \left({\frac {n+1}{2}}-1\right)}
A ,D 所在的x 座標)代入上面的方程式
(
n
+
1
2
−
1
)
2
+
y
2
=
(
n
+
1
2
)
2
{\displaystyle \left({\frac {n+1}{2}}-1\right)^{2}+y^{2}=\left({\frac {n+1}{2}}\right)^{2}}
解方程,得
y
=
n
{\displaystyle y={\sqrt {n}}}
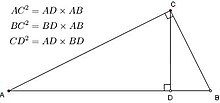
另也可参见射影定理 。
射影定理(图)
^ Analysis of YBC 7289 . ubc.ca. [19 January 2015] . (原始内容 存档于2020-03-12). ^ Anglin, W.S. (1994). Mathematics: A Concise History and Philosophy . New York: Springer-Verlag.
^ Heath, Sir Thomas L. The Thirteen Books of The Elements, Vol. 3 . Cambridge University Press. 1908: 3. ^ Abramowitz, Milton; Stegun, Irene A. Handbook of mathematical functions with formulas, graphs, and mathematical tables . Courier Dover Publications. 1964: 17. ISBN 0-486-61272-4存档 于2016-04-23). Section 3.7.27, p. 17 互联网档案馆 的存檔 ,存档日期2009-09-10.^ Cooke, Roger. Classical algebra: its nature, origins, and uses . John Wiley and Sons. 2008: 59. ISBN 0-470-25952-3存档 于2016-04-23). ^ 劳汉生《珠算与实用算术》ISBN 7-5375-1891-2 /O


















![{\displaystyle {\sqrt[{n}]{\,\,}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/ddcb8a480722f2e988fb8ebe5dfd905140a9a52a)
























![{\displaystyle {\begin{aligned}{\sqrt {i}}&=\left[\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)\right]^{\frac {1}{2}}\\&=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)\\&={\frac {\sqrt {2}}{2}}+i{\frac {\sqrt {2}}{2}}\\&={\frac {\sqrt {2}}{2}}(1+i)\end{aligned}}}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/1f86b3b7203a50d96454199f6b6b0ca30d029303)






































































![{\displaystyle {\sqrt {2}}=[1;2,2,2,2...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/5fc9b02798ffa8c81bf9bdcbc2f09e1e0aee4422)
![{\displaystyle {\sqrt {3}}=[1;1,2,1,2...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/df0c6eb26d9a8ea8fc7536e85d506c3970d25d3b)

![{\displaystyle {\sqrt {5}}=[2;4,4,4,4...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/3db0b9a3b70d460c26600c2a48038f4044f30bf2)
![{\displaystyle {\sqrt {6}}=[2;2,4,2,4...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/0a77c30771fc26826e8d2c5e7bed3f3a41850f47)
![{\displaystyle {\sqrt {7}}=[2;1,1,1,4,1,1,1,4...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/07f8ee5f5ca1b5e7fef75103bacd0ffbc18ab597)
![{\displaystyle {\sqrt {8}}=[2;1,4,1,4...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/f94114159ad39146dbee0db04f66f5fc6c5e15ed)
![{\displaystyle {\sqrt {10}}=[3;6,6,6,6...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/849b4bef93de145e137f648999d6d3c3fab2db5e)
![{\displaystyle {\sqrt {11}}=[3;3,6,3,6...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/bf1bddf4ae2a7b8fa8a47e8996cd6f109ddeb0ab)
![{\displaystyle {\sqrt {12}}=[3;2,6,2,6...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/d7f86b2454a2b20534e09dbe888b7228db1d8a44)
![{\displaystyle {\sqrt {13}}=[3;1,1,1,1,6,1,1,1,1,6...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/1270c1d403e3d9059ab4cf2c146ecb36c3dc08b0)
![{\displaystyle {\sqrt {14}}=[3;1,2,1,6,1,2,1,6...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/3d9a7e23c50b6c14119333421f27b7381250c7fe)
![{\displaystyle {\sqrt {15}}=[3;1,6,1,6...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/1883e99932565fc6b8e5a86a3934b130d3cb09be)

![{\displaystyle {\sqrt {17}}=[4;8,8,8,8...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/099316b44578e9592e1425571402bb24e76664fe)
![{\displaystyle {\sqrt {18}}=[4;4,8,4,8...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/d4a789b740adf75a585e1a4e3bb5d85a2fc23056)
![{\displaystyle {\sqrt {19}}=[4;2,1,3,1,2,8,2,1,3,1,2,8...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/c7cd3c48024a8f78a4b7ce606d442893d273e665)
![{\displaystyle {\sqrt {20}}=[4;2,8,2,8...]}](https://wikimedia.org/zhwiki/api/rest_v1/media/math/render/svg/d8ab7596515455a8476ccbcd6827283d0eab5ed0)












