叉积

關於其他常稱作外積的相關二元運算，參閱外積 (消歧義)。

叉積（英語：Cross product）是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。两个向量的叉积写作$\mathbf {a} \times \mathbf {b}$，也称作外积（英語：Outer product）或向量积（英語：Vector product）。叉积与原来的两个向量都垂直。

定义

在右手坐标系中的向量积

两个向量$\mathbf {a}$和$\mathbf {b}$的叉积写作 $\mathbf {a} \times \mathbf {b}$（有时也被写成$\mathbf {a} \wedge \mathbf {b}$，避免和字母x混淆）。叉积可以定义为：

$\mathbf {a} \times \mathbf {b} =\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin \theta \;{\hat {\mathbf {n} }}$

在这里$\theta$表示$\mathbf {a}$和$\mathbf {b}$之间的角度（$0^{\circ }\leq \theta \leq 180^{\circ }$），它位于这两个向量所定义的平面上。而${\hat {\mathbf {n} }}$是一个与$\mathbf {a}$、$\mathbf {b}$所构成的平面垂直的单位向量。

这个定义有个问题，就是同时有两个单位向量都垂直于$\mathbf {a}$和$\mathbf {b}$：若${\hat {\mathbf {n} }}$满足垂直的条件，那么$-{\hat {\mathbf {n} }}$也满足。

“正确”的向量由向量空间的方向确定，即按照给定直角坐标系的左右手定则。若（$\mathbf {i}$、$\mathbf {j}$、$\mathbf {k}$）满足右手定则，则（$\mathbf {a}$、$\mathbf {b}$、$\mathbf {a} \times \mathbf {b}$）也满足右手定则；或者两者同时满足左手定则。

一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系满足右手定则，当右手的四指从$\mathbf {a}$以不超过180°的转角转向$\mathbf {b}$时，竖起的大拇指指向是$\mathbf {a} \times \mathbf {b}$的方向。由于向量的叉积由坐标系确定，所以其结果被称为「伪向量」。

性质

代数性质

對於任意三個向量$\mathbf {a}$、$\mathbf {b}$、$\mathbf {c}$，

• $\mathbf {a} \times \mathbf {a} =\mathbf {0}$
• $\mathbf {a} \times \mathbf {0} =\mathbf {0}$
• $\mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} )$（反交换律）
• $\mathbf {a} \times (\mathbf {b} +\mathbf {c} )=\mathbf {a} \times \mathbf {b} +\mathbf {a} \times \mathbf {c}$（加法的左分配律）
• $(\mathbf {a} +\mathbf {b} )\times \mathbf {c} =\mathbf {a} \times \mathbf {c} +\mathbf {b} \times \mathbf {c}$（加法的右分配律）
• $(\lambda \mathbf {a} )\times \mathbf {b} =\lambda (\mathbf {a} \times \mathbf {b} )=\mathbf {a} \times (\lambda \mathbf {b} )$
• $\mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b}$
• $|\mathbf {a} \times \mathbf {b} |=|\mathbf {b} \times \mathbf {a} |$
• $|\mathbf {a} \times \mathbf {b} |^{2}=|\mathbf {a} |^{2}|\mathbf {b} |^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}={\begin{vmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{vmatrix}}$（拉格朗日恆等式）

一般來說，向量叉積不遵守約簡律，即$\mathbf {a} \times \mathbf {b} =\mathbf {a} \times \mathbf {c}$不表示$\mathbf {b} =\mathbf {c}$。此外，$\mathbf {a} \times \mathbf {b} =\mathbf {0}$不表示$\mathbf {a} =\mathbf {0}$或$\mathbf {b} =\mathbf {0}$。

但對於两个非零向量$\mathbf {a}$和$\mathbf {b}$，

• $\mathbf {a} \times \mathbf {b} =\mathbf {0}$當且僅當$\mathbf {a}$平行於$\mathbf {b}$

三重積

主条目：三重積

純量三重積满足以下特殊的结合律：

• $\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=(\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c}$

向量三重積不满足结合律，但满足以下恆等式：

• $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )\;+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )\;+\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0}$（雅可比恆等式）

向量三重積亦可以點積展開：

• $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$（拉格朗日公式）

向量微分

對於實數$t$和兩個向量值函數$\mathbf {a} (t)$、$\mathbf {b} (t)$，乘積法則成立：

• ${\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}}$

三維坐標

给定直角坐标系的单位向量$\mathbf {i}$，$\mathbf {j}$，$\mathbf {k}$满足下列等式：

$\mathbf {i} \times \mathbf {j} =\mathbf {k}$、$\mathbf {j} \times \mathbf {k} =\mathbf {i}$、$\mathbf {k} \times \mathbf {i} =\mathbf {j}$

通过这些规则，两个向量的叉积的坐标可以方便地计算出来，不需要考虑任何角度：设

$\mathbf {a} =a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k}$

$\mathbf {b} =b_{1}\mathbf {i} +b_{2}\mathbf {j} +b_{3}\mathbf {k}$

则

${\begin{aligned}\mathbf {a} \times \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} \\&={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}\end{aligned}}$

叉积也可以用四元数来表示。注意到上述$\mathbf {i}$、$\mathbf {j}$、$\mathbf {k}$之间的叉积满足四元数的乘法。一般而言，若将向量[a₁, a₂, a₃]表示成四元数a₁i + a₂j + a₃k，两个向量的叉积可以这样计算：计算两个四元数的乘积得到一个四元数，并将这个四元数的实部去掉，即为结果。更多关于四元数乘法，向量运算及其几何意义请参见四元数与空间旋转。

几何意义

以向量定義的平行四边形。

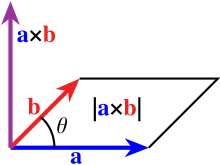
由向量$\mathbf {a}$和$\mathbf {b}$定義兩條鄰邊的平行四边形，其面積$A$為

$A=|\mathbf {a} ||\mathbf {b} |\sin \theta$

因此兩支向量叉積的模長可視作平行四边形其面積：

• $A=|\mathbf {a} \times \mathbf {b} |$

高维情形

七维向量的叉积可以通过八元数得到，与上述的四元数方法相同。

七维叉积具有与三维叉积相似的性质：

• 双线性性：

$\mathbf {x} \times (a\mathbf {y} +b\mathbf {z} )=a\mathbf {x} \times \mathbf {y} +b\mathbf {x} \times \mathbf {z}$

$(a\mathbf {y} +b\mathbf {z} )\times \mathbf {x} =a\mathbf {y} \times \mathbf {x} +b\mathbf {z} \times \mathbf {x}$

• 反交换律：

$\mathbf {x} \times \mathbf {y} +\mathbf {y} \times \mathbf {x} =\mathbf {0}$

• $\mathbf {x} \times \mathbf {y}$同时与$\mathbf {x}$和$\mathbf {y}$垂直：

$\mathbf {x} \cdot (\mathbf {x} \times \mathbf {y} )=\mathbf {y} \cdot (\mathbf {x} \times \mathbf {y} )=\mathbf {0}$

• 拉格朗日恒等式

$|\mathbf {x} \times \mathbf {y} |^{2}=|\mathbf {x} |^{2}|\mathbf {y} |^{2}-(\mathbf {x} \cdot \mathbf {y} )^{2}$

• 不同于三维情形，它并不满足雅可比恒等式：

$\mathbf {x} \times (\mathbf {y} \times \mathbf {z} )\;+\mathbf {y} \times (\mathbf {z} \times \mathbf {x} )\;+\mathbf {z} \times (\mathbf {x} \times \mathbf {y} )\neq \mathbf {0}$

应用

另外，在物理学力学、电磁学、光学和计算机图形学等理工学科中，叉积应用十分广泛。例如力矩、角动量、洛伦兹力等矢量都可以由向量的叉积求解。在进行这些物理量的计算时，往往可以借助右手定则辅助判断方向。

参见

• 純量积
• 三重積
• 右手定则
• 外代数：叉乘的实质，赝矢量与赝标量