蒸氣壓:修订间差异
外观
删除的内容 添加的内容
修飾語句 |
|||
| 第2行: | 第2行: | ||
{{NoteTA|G1=Chemistry}} |
{{NoteTA|G1=Chemistry}} |
||
{{Unreferenced|time=2014-07-18T00:40:49+00:00}} |
{{Unreferenced|time=2014-07-18T00:40:49+00:00}} |
||
一种物质的'''蒸气压'''也称作'''[[饱和蒸气压]]''',指的是这种物质的[[气相]]与其非气相达到平衡状态时的[[压强]]。任何物质(包括液态与固态)都有挥发成为气态的趋势,其气态也同样具有[[凝結]]为液态或者[[凝华]]为固态的趋势。在给定的温度下,一种物质的气态与其[[凝聚态]](固态或液态)之间会在某一个压强下存在动态平衡。此时单位时间内由气态转变为凝聚态的[[分子]]数与由凝聚态转变为气态的分子数相等。这个压强就是此物质在此温度下的饱和蒸气压 |
一种物质的'''蒸气压'''也称作'''[[饱和蒸气压]]''',指的是这种物质的[[气相]]与其非气相达到平衡状态时的[[压强]]。任何物质(包括液态与固态)都有挥发成为气态的趋势,其气态也同样具有[[凝結]]为液态或者[[凝华]]为固态的趋势。在给定的温度下,一种物质的气态与其[[凝聚态]](固态或液态)之间会在某一个压强下存在动态平衡。此时单位时间内由气态转变为凝聚态的[[分子]]数与由凝聚态转变为气态的分子数相等。这个压强就是此物质在此温度下的饱和蒸气压。 |
||
它们之间的关系可以用[[克劳修斯-克拉佩龙方程]](Clausius–Clapeyron relation)描述。随着温度的升高,物质蒸气压随之升高直到足以克服周围大气的压强从而在物质本体内的任何位置发生气化而产生大量气泡。这一现象叫做[[沸腾]],而这个温度叫做此压强下的[[沸点]]。物质的常压沸点就是此物质的饱和蒸气压等于一个[[标准大气压]]时候的温度。需要注意的是在较深液体中发生的沸腾所需温度会高于较浅液体中的沸腾,因为除了大气压强外还需要克服液体自身深度所造成的压强。對於[[溶液]],計算需用[[拉午耳定律]]。 |
|||
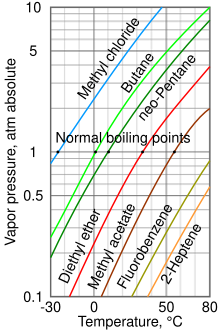
[[Image:vapor_pressure_chart.svg|thumb|right|數種不同的液體的[[蒸氣壓|蒸氣壓力]]對比。]] |
[[Image:vapor_pressure_chart.svg|thumb|right|數種不同的液體的[[蒸氣壓|蒸氣壓力]]對比。]] |
||
==使用安托萬方程計算蒸氣壓== |
==使用安托萬方程計算蒸氣壓== |
||
2019年10月6日 (日) 17:44的版本
此條目可参照外語維基百科相應條目来扩充。 (2017年5月21日) |
此條目没有列出任何参考或来源。 (2014年7月18日) |
一种物质的蒸气压也称作饱和蒸气压,指的是这种物质的气相与其非气相达到平衡状态时的压强。任何物质(包括液态与固态)都有挥发成为气态的趋势,其气态也同样具有凝結为液态或者凝华为固态的趋势。在给定的温度下,一种物质的气态与其凝聚态(固态或液态)之间会在某一个压强下存在动态平衡。此时单位时间内由气态转变为凝聚态的分子数与由凝聚态转变为气态的分子数相等。这个压强就是此物质在此温度下的饱和蒸气压。
它们之间的关系可以用克劳修斯-克拉佩龙方程(Clausius–Clapeyron relation)描述。随着温度的升高,物质蒸气压随之升高直到足以克服周围大气的压强从而在物质本体内的任何位置发生气化而产生大量气泡。这一现象叫做沸腾,而这个温度叫做此压强下的沸点。物质的常压沸点就是此物质的饱和蒸气压等于一个标准大气压时候的温度。需要注意的是在较深液体中发生的沸腾所需温度会高于较浅液体中的沸腾,因为除了大气压强外还需要克服液体自身深度所造成的压强。對於溶液,計算需用拉午耳定律。
使用安托萬方程計算蒸氣壓
安托萬方程是一個用來描述液體或固體的蒸氣壓與溫度的經驗表達式。安托萬方程的原始表達式如下:
將溫度項單獨移至等號左邊後可得:
其中:
- 為該物質的蒸氣壓。
- 為該物質的溫度。
- , 與 為與物質相關的係數 (可為常數或變數),每組, , 值只適用於特定物質的特定溫度範圍。
而上式在某些情況項又可以被化簡為如下:
總體來說,安托萬方程的使用上有許多限制。例如,該方程無法找出一組可適用於熔點與臨界溫度的範圍內的, 與 。另外,在建表當時的儀器導致該表於10托下的低壓環境也相當不精準。








