橢圓偏振技術:修订间差异
Pang-hung.liu(留言 | 贡献) 小 →基本原理 |
Pang-hung.liu(留言 | 贡献) |
||
| 第15行: | 第15行: | ||
===實驗裝置=== |
===實驗裝置=== |
||
[[Image:Ellipsometry.svg|thumb|right|400px|橢圓偏振實驗之裝置示意圖]] |
[[Image:Ellipsometry.svg|thumb|right|400px|橢圓偏振實驗之裝置示意圖]] |
||
[[光源]](Light Source)所放射出之[[電磁波]](Electromagnetic radiation)經過[[偏光鏡]](Polarizer)後,[[極化]]為[[線性偏振光]],可選擇是否通過補償鏡片(Compensator,[[延相器]]或[[四分之一波片]]),之後打在薄膜樣品上。電磁波被[[反射]]後同樣可選擇是否再通過補償鏡片,然後穿過第二片通常稱為分析鏡的偏光鏡,進入[[偵檢器]]。 有些橢圓儀不使用補償片,而在入射光束的路徑採用相位調變器。橢圓偏振是一種光學鏡面反射技術([[入射角]]等於[[反射角]]),入射光與反射光路徑在同一平面上(稱為入射平面),而被偏振為與此平面平行及垂直的光,則分別稱之為p或s偏振光。 |
[[光源]](Light Source)所放射出之[[電磁波]](Electromagnetic radiation)經過[[偏光鏡]](Polarizer)後,[[極化]]為[[線性偏振光]],可選擇是否通過補償鏡片(Compensator,[[延相器]]或[[四分之一波片]]),之後打在薄膜樣品上。電磁波被[[反射]]後同樣可選擇是否再通過補償鏡片,然後穿過第二片通常稱為分析鏡的偏光鏡,進入[[偵檢器]]。 有些橢圓儀不使用補償片,而在入射光束的路徑採用相位調變器。橢圓偏振是一種光學鏡面反射技術([[入射角]]等於[[反射角]]),入射光與反射光路徑在同一平面上(稱為入射平面),而被偏振為與此平面平行及垂直的光,則分別稱之為「p」或「s」偏振光。 |
||
===數據蒐集=== |
|||
(標準) 橢圓偏振測量四個史托克參數(Stokes parameters[http://en.wikipedia.org/wiki/Stokes_parameters])中的兩個, 通常以<math>\Psi</math> 及 <math>\Delta</math>來表示。入射至樣品的光之偏極化狀態可被分解成「s」及「p」兩項(「s」成份為光之電場振盪垂直入射平面,「p」則平行)。「s」及「p」成份之振幅(強度)在[[反射]]及對其初始值做正規化之後,分別標示為<math>r_s</math>及<math>r_p</math>。橢圓偏振測量<math>r_s</math>與<math>r_p</math>之比例,此比例可以下述基本方程式來描述: |
|||
:<math>\rho = \frac{r_p}{r_s} = \tan ( \Psi ) e^{i \Delta}</math> |
|||
其中,<math>\tan \Psi</math>為[[反射]]後之振幅比,<math>\Delta</math>為相位移(相差)。由於橢圓偏振係測量兩項之比值(或差異)而非其絕對數值,因此這技術所得的數據是相當正確且可再現的,其對散射及擾動等因素較不敏感,且不需要標準樣品或參考樣品。 |
|||
===數據分析=== |
|||
橢圓偏振為間接量測的技術,也就是說,一般測得的 <math>\Psi</math> 及 <math>\Delta</math> 並不能直接轉換為樣品的光學常數,通常需要建構模型來進行分析。只有對於無限厚、[[等向性]]且均勻的膜,才可能直接轉換得到其 <math>\Psi</math> 與 <math>\Delta</math> 之數值。在所有其他的情形下,則必需建構其層狀模型,並考慮所有各層之各別的光學常數如([[折射率]] 或 [[介電常數]])及厚度,且依正確的層畳順序建立。再藉由多次最小方差法最適化,變動未知的光學常數及(或)厚度參數,以之代入[[Fresnel方程式]]計算求得其對應 <math>\Psi</math> 及 <math>\Delta</math> 數值。最後,所得最接近實驗數據之 <math>\Psi</math> 及 <math>\Delta</math> 數值,其參數來源的光學常數及(或)厚度可視為此量測之最適化結果。 |
|||
[[de:Ellipsometrie]] |
[[de:Ellipsometrie]] |
||
2008年1月18日 (五) 21:28的版本
模板参数错误!(代码36)
|
此條目没有列出任何参考或来源。 (2007年10月12日) |
橢圓偏振技術是一種多功能和強大的光學技術,可用以取得薄膜的介電性質(複數折射率或介電常數)。它已被應用在許多不同的領域,從基礎研究到工業應用,如半導體物理研究、微電子學和生物學。橢圓偏振是一個很敏感的薄膜性質測量技術,且具有非破壞性和非接觸之優點。
分析自樣品反射之極化光的改變,橢圓偏振技術可得到膜厚比探測光本身波長更短的薄膜資訊,小至一個單原子層,甚至更小。橢圓儀可測得複數折射率或介電函數張量,可以此獲得基本的物理參數,並且這與各種樣品的性質,包括形態、晶體質量、化學成分或導電性,有所關聯。它常被用來鑑定單層或多層堆疊的薄膜厚度,可量測厚度由數埃(Angstrom)或數十奈米到幾微米皆有極佳的準確性。
之所以命名為橢圓偏振,是因為一般大部分的極化多是橢圓的。此技術已發展近百年,現在已有許多標準化的應用。然而,橢圓偏振技術對於在其他學科如生物學和醫學領域引起研究人員的興趣,並帶來新的挑戰。例如以此測量不穩定的液體表面和顯微成像。
基本原理
此技術係在測量光在反射或穿透樣品時,其偏振性質的改變。通常,橢圓偏振多在反射模式下進行。偏振性質的改變主要是由樣品的性質來決定(厚度、複折射率或介電性質(Dielectric function))。雖然光學技術受制於先天繞射極限的限制,橢圓偏振卻可藉由相位資訊及光偏振之狀態的改變,來取得埃等級的解析度。在最簡單的形式,此技術可適用於厚度小於一奈米到數微米之薄膜。樣品必須是由少數幾個不連續而有明確介面、光學均勻且具等向性且非吸收光的膜層構成。逾越上述的假設,則會不符標準橢圓偏振之處理程序,因而將需要對此技術更進階的一些改變以符合其應用(見下詳述)。
實驗細節
實驗裝置
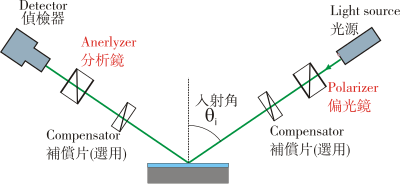
光源(Light Source)所放射出之電磁波(Electromagnetic radiation)經過偏光鏡(Polarizer)後,極化為線性偏振光,可選擇是否通過補償鏡片(Compensator,延相器或四分之一波片),之後打在薄膜樣品上。電磁波被反射後同樣可選擇是否再通過補償鏡片,然後穿過第二片通常稱為分析鏡的偏光鏡,進入偵檢器。 有些橢圓儀不使用補償片,而在入射光束的路徑採用相位調變器。橢圓偏振是一種光學鏡面反射技術(入射角等於反射角),入射光與反射光路徑在同一平面上(稱為入射平面),而被偏振為與此平面平行及垂直的光,則分別稱之為「p」或「s」偏振光。
數據蒐集
(標準) 橢圓偏振測量四個史托克參數(Stokes parameters[1])中的兩個, 通常以 及 來表示。入射至樣品的光之偏極化狀態可被分解成「s」及「p」兩項(「s」成份為光之電場振盪垂直入射平面,「p」則平行)。「s」及「p」成份之振幅(強度)在反射及對其初始值做正規化之後,分別標示為及。橢圓偏振測量與之比例,此比例可以下述基本方程式來描述:
其中,為反射後之振幅比,為相位移(相差)。由於橢圓偏振係測量兩項之比值(或差異)而非其絕對數值,因此這技術所得的數據是相當正確且可再現的,其對散射及擾動等因素較不敏感,且不需要標準樣品或參考樣品。
數據分析
橢圓偏振為間接量測的技術,也就是說,一般測得的 及 並不能直接轉換為樣品的光學常數,通常需要建構模型來進行分析。只有對於無限厚、等向性且均勻的膜,才可能直接轉換得到其 與 之數值。在所有其他的情形下,則必需建構其層狀模型,並考慮所有各層之各別的光學常數如(折射率 或 介電常數)及厚度,且依正確的層畳順序建立。再藉由多次最小方差法最適化,變動未知的光學常數及(或)厚度參數,以之代入Fresnel方程式計算求得其對應 及 數值。最後,所得最接近實驗數據之 及 數值,其參數來源的光學常數及(或)厚度可視為此量測之最適化結果。







