不连续点

不连续点是指：在非连续函数y=f(x)中某点处x_o处有中断现象，那么，x_o就称为函数的不连续点。

分类

根据不同不连续点的性质，通常把不连续点分为两类：

1. 第一类不连续点：
   1. 跳跃不连续点：不连续点两侧函数的极限存在，但不相等；
   2. 可去不连续点：不连续点两侧函数的极限存在且相等。
2. 第二类不连续点：

不属于第一类不连续点的任何一种不连续点都属于第二类不连续点。

例子

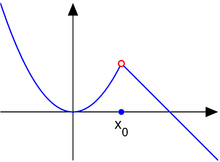可去不连续点

1. 考虑以下函数：

$f(x)={\begin{cases}x^{2}&{\mbox{ for }}x<1\\0&{\mbox{ for }}x=1\\2-x&{\mbox{ for }}x>1\end{cases}}$

点$x_{0}=1$是可去不连续点。

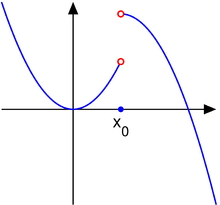跳跃不连续点

2. 考虑以下函数：

$f(x)={\begin{cases}x^{2}&{\mbox{ for }}x<1\\0&{\mbox{ for }}x=1\\2-(x-1)^{2}&{\mbox{ for }}x>1\end{cases}}$

点$x_{0}=1$是跳跃不连续点。

第二类不连续点

3. 考虑以下函数：

$f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\mbox{ for }}x<1\\0&{\mbox{ for }}x=1\\{\frac {0.1}{x-1}}&{\mbox{ for }}x>1\end{cases}}$

点$x_{0}=1$是第二类不连续点，又称本性不连续点。