P/NP问题:修订间差异
小 robot Adding: fi |
无编辑摘要 |
||
| 第11行: | 第11行: | ||
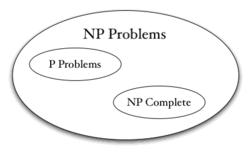
[[NP-完全]]问题(或者叫'''NPC''')的集合在这个讨论中有重大作用,它们可以大致的被描述为那些在'''NP'''中最不像在'''P'''中的。(确切定义细节请参看[[NP-完全]])理论[[计算机科学家]]现在相信'''P''', '''NP''',和'''NPC'''类之间的关系如图中所示,其中'''P'''和'''NPC'''类不交。 |
[[NP-完全]]问题(或者叫'''NPC''')的集合在这个讨论中有重大作用,它们可以大致的被描述为那些在'''NP'''中最不像在'''P'''中的。(确切定义细节请参看[[NP-完全]])理论[[计算机科学家]]现在相信'''P''', '''NP''',和'''NPC'''类之间的关系如图中所示,其中'''P'''和'''NPC'''类不交。 |
||
本质上,'''P''' = '''NP'''问题问道:如果是/不是问题的正面答案可以很快''验证'',其答案是否也可以很快''计算''?这里有一个给你找点这个问题的感觉的例子。给定一个大数''Y'',我们可以问''Y''是否是[[复合数]]。例如,我们可能问53308290611是否有非平凡的因子。回答是肯定的,虽然手工找出一个因子很麻烦。从另一个方面讲,如果有人声称答案是"对,因为224737可以整除53308290611",则我们可以很快用一个除法来验证。验证一个数是除数比首先找出除数来简单得多。用于验证一个正面答案所需的信息也称为''证书''。所以我们的结论是,给定 正确的证书,问题的正面答案可以很快的(也就是,在多项式时间内)验证,而这就是这个问题属于'''NP'''的原因。虽然这个特定的问题,最近被证明为也在'''P'''类中(参看[[#外部链接和参考|下面的]]关于"质数在P中"的参考),这一点也不明显,而且有很多类似的问题相信不属于类'''P'''。 |
本质上,'''P''' = '''NP'''问题问道:如果是/不是问题的正面答案可以很快''验证'',其答案是否也可以很快''计算''?这里有一个给你找点这个问题的感觉的例子。给定一个大数''Y'',我们可以问''Y''是否是[[合数|复合数]]。例如,我们可能问53308290611是否有非平凡的因子。回答是肯定的,虽然手工找出一个因子很麻烦。从另一个方面讲,如果有人声称答案是"对,因为224737可以整除53308290611",则我们可以很快用一个除法来验证。验证一个数是除数比首先找出除数来简单得多。用于验证一个正面答案所需的信息也称为''证书''。所以我们的结论是,给定 正确的证书,问题的正面答案可以很快的(也就是,在多项式时间内)验证,而这就是这个问题属于'''NP'''的原因。虽然这个特定的问题,最近被证明为也在'''P'''类中(参看[[#外部链接和参考|下面的]]关于"质数在P中"的参考),这一点也不明显,而且有很多类似的问题相信不属于类'''P'''。 |
||
限制到是/不是问题并没有改变问题;即使我们允许更复杂的答案,最后的问题(是否[[FP (复杂度)|FP]] = [[FNP (复杂度)|FNP]])是等价的。 |
限制到是/不是问题并没有改变问题;即使我们允许更复杂的答案,最后的问题(是否[[FP (复杂度)|FP]] = [[FNP (复杂度)|FNP]])是等价的。 |
||
2005年12月7日 (三) 08:11的版本
| 千禧年大獎難題 |
|---|
模板参数错误!(代码36)
|
计算复杂度理论是计算理论处理解决给定问题所需的资源的一部分。最常见的资源就是时间(解决问题的步数)和空间(需要多少内存来解决问题)。
在这个理论中,类P有所有那些可以在一个确定序列化机器上一和输入大小的多项式表达的时间内解决的决定问题组成;类NP有所有其肯定解可以在给定正确信息的多项式时间内验证的决定问题组成,或者等效的说,那些解可以在非确定图灵机上在多项式时间内找出的问题的集合。很可能,计算理论最大的未解决问题就是关于这两类的关系的:
- P和NP相等吗?
在2002年对于100研究者的调查,61人相信答案是否定的,9个相信答案是肯定的,22个不确定,而8个相信该问题可能和现在所接受的公理独立,所以不可能证明或证否。[1] 对于正确的解答,有一个$1,000,000美元的奖励。
NP-完全问题(或者叫NPC)的集合在这个讨论中有重大作用,它们可以大致的被描述为那些在NP中最不像在P中的。(确切定义细节请参看NP-完全)理论计算机科学家现在相信P, NP,和NPC类之间的关系如图中所示,其中P和NPC类不交。
本质上,P = NP问题问道:如果是/不是问题的正面答案可以很快验证,其答案是否也可以很快计算?这里有一个给你找点这个问题的感觉的例子。给定一个大数Y,我们可以问Y是否是复合数。例如,我们可能问53308290611是否有非平凡的因子。回答是肯定的,虽然手工找出一个因子很麻烦。从另一个方面讲,如果有人声称答案是"对,因为224737可以整除53308290611",则我们可以很快用一个除法来验证。验证一个数是除数比首先找出除数来简单得多。用于验证一个正面答案所需的信息也称为证书。所以我们的结论是,给定 正确的证书,问题的正面答案可以很快的(也就是,在多项式时间内)验证,而这就是这个问题属于NP的原因。虽然这个特定的问题,最近被证明为也在P类中(参看下面的关于"质数在P中"的参考),这一点也不明显,而且有很多类似的问题相信不属于类P。
